Тема 3. Лекция 10. Решение антагонистических игр на основе удаления доминируемых стратегий. Принцип доминирования

Рассмотрим один из способов реду­цирования игр, основанный на принципе доминирования, который позволяет в некоторых случаях игру с матрицей большего размера свести к игре с мат­рицей меньшего размера.

Пусть имеем игру с матрицей A размера m*n.

Bj Ai	B1	B2	…	Bn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…	…	…	…
Am	am1	am2	…	amn

Каждой смешанной (в частности, чистой) стратегии Р=(р1, р2,…, рm) игрока A поставим в соответствие строку

(H(P, B1), H(P, B2),…, H(P, Bn)) (2.11.1)

(размера 1хn), элементами которой являются выигрыши H(P, Bj), j=1,2,…,n, игрока А в ситуациях (P, Bj), j=1,2,…,n.

Строку (2.11.1) можно представить так:

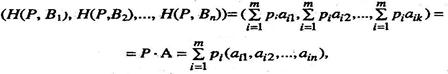(2.11.2.)

откуда видно, что она является выпуклой комбинацией строк матрицы А (выпуклой потому, что коэффициенты р1, р2,…, рm неотрицательны и в сумме дают единицу).

Обратно, каждой выпуклой комбинации (2.11.2) строк матрицы А с коэффи­циентами р1, р2,…, рm поставим в соответствие смешанную стратегию Р=(р1, р2,…, рm) игрока А.

Таким образом, между смешанными (в том числе и чистыми) стратегиями
Р=(р1, р2,…, рm) игрока A и выпуклыми комбинациями

строк (а i1, а i2,…, а in), i=l,,.., m, матрицы А устанавливается взаимно-однозначное соответствие

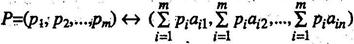(2.11.3.)

Из (2.11.1) или (2.11.3) ясно, что каждой чистой стратегии A_k, k =l, 2,...,m, игрока А ставится во взаимно-однозначное соответствие k-я строка (а k1, а k2,…, а kn), матри­цы А.

Если для двух выпуклых комбинаций строк матрицы А

(2.11.4.)

и

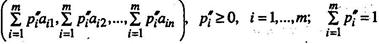(2.11.5.)

выполняются неравенства:

(2.11.6.)

то говорят, что строка (2.11.5) доминирует строку (2.11.4), а строка (2.11.4) до­минируется строкой (2.11.5). Таким образом, строка (2.11.5) — доминирующая строку (2.11.4), а строка (2.11.4) — доминируемая строкой (2. 11. 5).

Если каждое из неравенств (2.11.6) является равенством, то строки (2.11.4) и (2.11.5) называют дублирующими друг друга. Каждая из двух дублирующих строк является одновременно и доминируемой, и доминирующей другую.

Если каждое из неравенств (2.11.6) является строгим, то говорят, что строка (2.11.5) строго доминирует строку (2.11.4), а строка (2.11.4) строго доминируется строкой (2.11.5), или строка (2.11.5) является строго доминирующей строку (2.11.4), а строка (2.11.4) является строго доминируемой строкой (2.11.5).

Аналогичная терминология используется и для соответствующих стратегий игрока А. А именно, если строка (2.11.5) доминирует, соответственно дублирует, соответственно строго доминирует строку (2.11.4), то говорят, что стратегия Р" = (р1", р2",…, рn") доминирует, соответственно дублирует, соответственно строго доминирует стратегию Р' = (p1', p2',…, pn').

Так как элементами строк, соответствующих по (2.11.3) смешанным стратеги­ям, являются выигрыши игрока А (см. (2.11.1)), то из данных определений понят­но, что для игрока А дублирующие стратегии равнопредпочтительны, а домини­руемая не дублирующая стратегия заведомо для него невыгодна.

Аналогично, каждой смешанной (в частности, чистой) стратегии Q=(q1, q2,…, qn) игрока В поставим в соответствие столбец

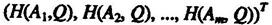(2.11.7.)

(размера mx1) его проигрышей H(Ai, Q), i=1,..., m, в ситуациях (Ai, Q), i=1,..., m. Ис­пользуя формулы (2.8.7), столбец (2.11.7) можно представить следующим образом:

(2.11.8.)

Отсюда видно, что столбец (2.11.7) является выпуклой комбинацией столбцов 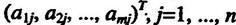, матрицы A с коэффициентами q1, q2,…, qn.

Обратно, каждой выпуклой комбинации (2.11.8) столбцов матрицы А с коэффициентами:

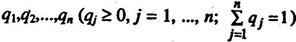
Поставим в соответствие смешанную стратегию Q=(q1, q2,…, qn) игрока В.

Таким образом, между смешанными и чистыми стратегиями Q=(q1, q2,…, qn) € Sb игрока В и выпуклыми комбинациями

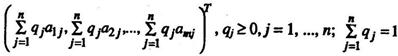
столбцов 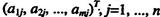, матрицы А устанавливается взаимно-однозначное соответствие

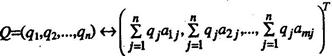(2.11.9.)

По которому, в частности, каждой чистой стратегии Bl, l=1,…,n, игрока В ставится во взаимно-однозначное соответствие l-й столбец матрицы А (см. также(2.11.7.)).

Если для двух выпуклых комбинаций столбцов матрицы А

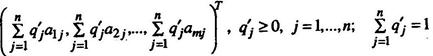(2.11.10)

и

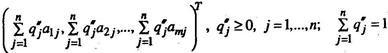(2.11.11.)

справедливы неравенства

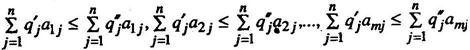(2.11.12.)

то говорят, что столбец (2.11.10) (стратегия Q' = (q1', q2',…, qn')) доминирует столбец (2.11.11) (стратегию Q" = (q1", q₂",..., q_n")), а столбец (2.11.11) (страте­гия Q") доминируется столбцом (2.11.10) (стратегией Q').

В случае, когда каждое неравенство (2.11.12) является равенством, столбцы (2.11.10) и (2.11.11) (стратегии Q' и Q") называются дублирующими.

Если каждое неравенство (2.11.12) является строгим, то столбец (2.11.10) (стратегия Q') называется строго-доминирующим (строго доминирующей) стол­бец (2.11.11) (стратегию Q"), а столбец (2.11.11) (стратегия Q") — строго доми­нируемым (строго доминируемой) столбцом (2.11.10) (стратегией (Q').

Поскольку элементами столбцов, соответствующих по (2.11.9) смешанным стратегиям игрока В, являются его проигрыши, то для него дублирующие страте­гии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо невыгодна.

Таким образом, по данным определениям и для игрока А, и для игрока В предпочтительными оказываются доминирующие стратегии.

Теорема 1 Справедливы следующие предложения:

1) Если k-я строка, k€ ۟ {l,...,m}, матрицы А игры, доминируется некоторой вы­пуклой комбинацией остальных ее строк, то существует оптимальная смешанная
стратегия 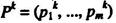игрока А, в которой k-я чистая стратегия Ak выбирается
им с нулевой вероятностью, т.е. .

2) Если k-я строка, k€ ۟ {l,...,m}, матрицы А игры, строго доминируется некото­рой выпуклой комбинацией остальных ее строк, то в любой оптимальной сме­шанной стратегии Р° = (p1°,..., pm°) игрока А чистая k-я стратегия Ak выбирается
им с нулевой вероятностью, т.е. рk° = 0.

3) Если l-й столбец, l€{1,...,n), матрицы А игры, доминируется некоторой вы­пуклой комбинацией остальных ее столбцов, то существует оптимальная смешан­ная стратегия 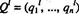игрока В, в которой l-я чистая стратегия Вl выбира­ется им с нулевой вероятностью, т.е. ql =0.

4) Если 1-й столбец, l€{1,...,n}, матрицы A игры, строго доминируется некото­рой выпуклой комбинацией остальных ее столбцов, то в любой оптимальной
смешанной стратегии Q°= (q1°,..., qn°) игрока В, чистая 1-я стратегия Вl выбирает­ся им с нулевой вероятностью, т.е. q1° =0

Утверждение 2) теоремы 2.11.1 означает, что если k-я строка матрицы игры строго доминируется некоторой выпуклой комбинацией остальных ее строк, то ее нужно удалить, поскольку чистая стратегия Ak априори невыгодна игроку А.

Аналогичные замечания относятся к доминируемым столбцам матрицы игры в утверждениях 3) и 4).

Дата добавления: 2014-01-04