В 6. Особенности малой выборки

В перерабатывающей промышленности и в сельском хозяйстве, где необходимо установить качество продукции используют метод оценки проб продукции в лабораторных условиях. Как правило, количество проб небольшое. В каждом конкретном случае экспериментальным способом отрабатывались методики взятия проб и оценки качества продукции.

Малой выборкой считают выборку, объем которой находится в пределах от 5 до 30 единиц, т.е. 5<n£30.

При малой выборке нельзя принимать равенство дисперсий 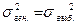, как это делается для большой выборки. Особенность малой выборки в том, что ее случайные ошибки не подчиняются закону нормального распределения.

Закон распределения случайных ошибок малой выборки был найден английским ученым Вильямом Госсетом (1876–1937) и опубликован в 1908 г. под псевдонимом «Стьюдент».

Для малой выборки расчет предельной ошибки выборки найдем по формуле:

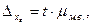(5.12)

где 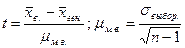– стандартная ошибка малой выборки.

Разность (n-1) называется числом степеней свободы и обозначается ν=n–1. В некоторых учебниках эта разность обозначается буквой k.

Стьюдентом разработаны таблицы, которыми все пользуются для определения предельного значения t, при различных значениях вероятности (Р).

Современные таблицы Стьюдента, которые имеются в каждом учебнике статистики и теории вероятностей, более подробные.

Объем выборки (n)	Р=0,95	Р=0,99
…	3,18 2,78 2,57 ......	5,84 4,60 4,03 ........

Рассмотрим несколько задач по выборочному наблюдению.

Задача 1.

Для определения средней урожайности картофеля в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25.

Таблица 5.3. Результаты обследования по районам.

№ района	Средняя урожайность, ц с 1 га	Посевная площадь, га	Валовой сбор, тыс.ц.
	fi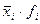
Итого, в среднем

Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность картофеля по области.

Дата добавления: 2014-01-04