В 9. История развития многофакторного корреляционно-регрессионного анализа

Начало корреляционного и регрессионного анализа относится ко второй половине ХIХ века и связано с именем двоюродного брата Ч. Дарвина – Френсисом Гальтоном (1822–1911). Он ввел понятие «закона регрессии», связав его со средним снижением роста сыновей по сравнению с ростом отцов (1899 г). Ему же принадлежит введение числовой меры, оценивающей силу связи показателей (корреляцию). Поэтому началом разработки корреляционно-регрессионного анализа ученые–статистики считают статью Ф. Гальтона «Регрессия, наследственность и панмиксия» (1896 г), в которой автор «дал определение корреляции, построил теоретическую модель совместного измерения двух переменных, ввел понятие линии регрессии и корреляционного индекса «r».

Экономистами и математиками разработаны различные модели, оценивающие влияние нескольких факторов на результат. Например, в США в 1929 г. при анализе развития обрабатывающей промышленности за 1899–1922 гг. была построена мультипликативная производственная функция, отражающая зависимость выхода продукции от затрат живого труда и наличия капитала, которая получила название функции Кобба-Дугласа (там же, с.176):

У= а L^α K^β, (6.39)

где У – объем выпускаемой продукции, а – коэффициент размерности, L – объем затрат живого труда или численность работников, К – объем капитала (основного или совокупного), α и β – коэффициенты эластичности производства продукции по труду и капиталу.

Для сельского хозяйства данную модель можно расширить, включив в нее еще один важный ресурс – это площадь сельскохозяйственных угодий (S) с соответствующим коэффициентом эластичности. Тогда данная функция будет иметь вид:

У=аL^αK^βS^γ, (6.40)

Существуют и другие нелинейные модели, отражающие различные связи факторов, некоторые из которых рассматриваются в курсе «Планирование и прогнозирование». Однако большинство из них не могут быть интерпретированы системой экономических параметров и сложны в экономическом обосновании.

Например, что может отражать экономический логарифм производительности труда или производительность труда в степени n и так далее? То есть модели могут быть использованы для прогнозов без экономической интерпретации параметров. Наилучшим образом экономически интерпретируется многофакторные линейные модели вида:

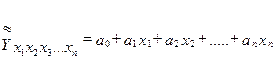(6.41)

где: n – отражает число факторов.

При составлении модели встает вопрос отбора факторов, которые могут быть включены в многофакторную модель. Как правило, имеется таблица с базой данных, где указаны числовые значения факторов интересующих исследователя. Общий вид такой таблицы с информацией о значениях технико-экономических показателей следующий:

Таблица 6.3. База данных для исследования связей факторов

№ п/п	Y	X1	X2	.....	Xn
				.....
				.....
...				.....
N

При исследовании необходимо решить целый ряд проблем, одна из которых заключается в отборе факторов для их включения в модель (уравнение регрессии). Здесь существенную роль играют знания исследователя об экономических закономерностях развития процессов и явлений, знания экономики конкретной отрасли (сельского хозяйства легкой и тяжелой промышленности, транспорта и т.д.). После сбора информации и проведения ее априорного анализа можно провести расчеты, позволяющие достаточно качественно отобрать факторы для проведения корреляционно-регрессионного анализа.

Для отбора факторов для модели часто используют матрицу парных коэффициентов корреляции, расчет и интерпретация которых рассматривалась в вопросах 5 и 6 темы.

Таблица 6.4. Матрица парных коэффициентов корреляции

	Y	X1	X2	.....	Xn
Y		rYX1	rYX2	.....	rYXn
X1			rX1X2	.....	rX1Xn
X2				.....	rX2Xn
....				.....	.....
Xn

Матрицу используют следующим образом:

По строке Y анализируют значения парных коэффициентов корреляции r_ij и отбирают в модель те факторы, для которых r_iy>0,2.

Используя остальные строки матрицы, устанавливают наличие или отсутствие мультиколлинеарности факторов. Если выявляется наличие таких пар факторов, то в модель включают только один из них.

Факторы являются мультиколлинеарными, если связь между ними близка к функциональной или функциональна.

Например, производительность труда и трудоемкость –показатели обратные друг другу, и для них парный коэффициент корреляции равен единице. В модель можно включить только один из этих факторов.

Можно считать, что фактор является незначимым, если его включение в уравнение регрессии только изменяет значение коэффициентов регрессии, не изменяя суммы квадратов остатков, то есть:

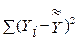= const (6.42)

Если при включении в модель факторного признака увеличивается величина множественного коэффициента корреляции и детерминации, а коэффициенты регрессии меняются незначительно, то данный признак существенен, и его включение в уравнение регрессии обязательно.

Дата добавления: 2014-01-04