В 11. Оценка тесноты связи признаков и ранжир факторов по силе их влияния на результат в множественном корреляционно-регрессионном анализе

Оценка тесноты связи Y со всеми X_i производится с помощью совокупного коэффициента (или индекса) детерминации:

, (6.44)

где факторная дисперсия

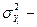общая дисперсия

остаточная дисперсия

и совокупного коэффициента корреляции:

(6.45)

Совокупный коэффициент детерминации R² может быть выражен в процентах. Он показывает, какая часть вариации результативного показателя объясняется вариацией факторов, включенных в модель.

Совокупный коэффициент корреляции всегда 0<R<1. Он отражает только тесноту связи и не может отражать направление связи (как парный коэффициент корреляции). Чем ближе значение R к 1, тем влияние факторов на результат сильнее, чем ближе к 0 – тем влияние слабее.

Расчет совокупного коэффициента детерминации можно произвести, используя связь его с парными коэффициентами корреляции r_ij и коэффициентами регрессии в стандартизированном виде, т.е. β –коэффициенты (см. вопрос 14)

(6.46)

Если рассматривается зависимость результата от двух факторов, то расчет совокупных коэффициентов корреляции и детерминации можно упростить, используя значения парных коэффициентов корреляции и детерминации.

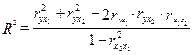(6.47)

При множественной корреляционно-регрессионной связи необходимо выделить тесноту связи результативного показателя индивидуально с каждым фактором, для чего вычисляют коэффициенты раздельной корреляции и детерминации.

Коэффициентом раздельной детерминации называется произведение парного коэффициента корреляции фактора Хi на его β –коэффициент

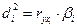(6.48)

Последняя формула отражает тоже равенство, что и формула (6.46). Корень квадратный из коэффициента раздельной детерминации даст коэффициент раздельной корреляции.

(6.49)

При построении уравнения регрессии важным моментом является последовательность включения факторов в уравнение регрессии. И здесь большую роль играет системная связь между каждой парой факторов, включенных в модель, и их группами. Поэтому важным представляется выделение дополнительной доли вариации результативного показателя (У) после включения в модель дополнительно фактора Х_к. Такая вариация объясняется частными коэффициентами корреляции и детерминации.

В общем виде частный индекс или коэффициент детерминации находят по формуле:

(6.50)

Как правило, частные коэффициенты корреляции и детерминации меньше парных коэффициентов корреляции и детерминации.

В случает анализа модели У по двум факторам Х₁ и Х₂ для расчета частных коэффициентов корреляции можно использовать следующие формулы:

(6.51)

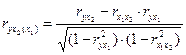(6.52)

В формуле 6.51 отражена связь между У и Х1 при условии неизменности Х2, в формуле 6.52 – связь между У и Х2 при условии постоянства Х1.

Частные коэффициенты детерминации найдем, возведя в квадрат частные коэффициенты корреляции. Их сумма близка к значению совокупного коэффициента детерминации.

Однако не следует упрощать смысл анализируемых показателей связи, т.к. вопросы анализа силы влияния факторов на результативный показатель можно рассматриваться в зависимости от последовательности включения факторов в модель от их «системного» влияния и т.д. Многие проблемные вопросы оценки силы влияния факторов на результативный показатель рассматриваются в современных учебниках статистики российских авторов.

Следующая группа показателей, отражающих связи факторов, включенных в модель, – это коэффициенты эластичности и – коэффициенты.

Коэффициенты эластичности вычисляются на базе первых частных производных от функции связи.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится результат (У) при изменении фактора Х_i в среднем на 1 % при условии неизменности остальных факторов, входящих в модель.

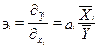(6.53)

(6.54)

– коэффициент показывает, на сколько среднеквадратических отклонений изменяется результат (У) при изменении фактора Х_i на одно свое среднеквадратическое отклонение, при неизменности остальных факторов входящих в уравнение.

Примечание:

Для парной линейной регрессии выполняется равенство 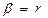. Поэтому в парном корреляционно-регрессионном анализе – коэффициент не рассматривался.

В 12. Оценка достоверности результатов произведенного корреляционно-регрессионного анализа.

Одним из требований при построении многофакторных моделей является требование к объему анализируемой совокупности, т.е. выборка должна быть репрезентативной (представительной). Однако это требование не всегда выполняется. Поэтому рассмотрим вопросы оценки достоверности полученных параметров уравнения и тесноты связи как для достаточно большой совокупности, так и для малой выборки.

а) Для репрезентативной выборки:

Оценка происходит по той же схеме, что и при парной линейной зависимости, для чего могут быть использованы критерий Стьюдента и критерий Фишера.

Расчет параметров t-критерия и F-критерия. Для каждого частного коэффициента регрессии рассчитывается значение t-критерия по формуле:

(6.55)

где в знаменателе стоит дисперсия частного коэффициента регрессии

(6.56)

где: R_i — величина множественного коэффициента корреляции по фактору X_i c остальными факторами.

Однако проще использовать F-критерий, т.к. с его помощью можно оценить достоверность всех полученных показателей (параметров и числовых характеристик).

(6.57)

где: n — число факторов в модели,

N – объем совокупности.

Табличное значение F-критерия найдем по таблицам Фишера, определив столбец по значению числа степеней свободы ν₁=n+1, строку – по ν₂=N-n-1.

Если F_расч.>=F_табл., то нуль-гипотеза отвергается и подтверждается достоверность произведенного корреляционно-регрессионного анализа.

Если при построении модели используется только два фактора (Х₁ и Х₂), то можно использовать упрощенную формулу

F_расч.= (6.58)

Табличное значение F-критерия находим по значениям ν₁=2, ν₂=N-3.

ν₁ – определяет графу,

ν₂ – строку таблицы.

б) Для малой выборки:

При небольшом числе наблюдений (а это часто бывает при исследовании небольшой совокупности, например, только по хозяйствам одного-двух районов), величина множественного коэффициента корреляции и детерминации завышается. Поэтому чтобы оценить реальную тесноту связи и ее достоверность, необходимо произвести следующие расчеты. Сначала проверим выполнение соотношения

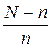>= 20

Если это соотношение выполняется, то все дальнейшие расчеты выполняем по пункту а), если не выполняется, то необходимо скорректировать значение множественного коэффициента корреляции и оценить его достоверность.

Рассчитаем скорректированный совокупный коэффициент корреляции

(6.59)

Произведем оценку достоверности скорректированного множественного коэффициента корреляции, используя формулы (6.57) или (6.58) и соответствующий алгоритм использования критерия Фишера.

Дата добавления: 2014-01-04