В 14. Стандартизированный вид уравнения связи

В 13. Прогнозирование по корреляционно-регрессион-ной модели.

Поскольку корреляционно-регрессионные модели статичны, то есть привязаны к месту и времени, то они обеспечивают прогноз на небольшом временном интервале при стабильных условиях экономической ситуации.

Различают прогнозы:

1. Наилучшие.

2. Наихудшие.

3. Усредненные.

Наилучшего значения результат Y будет достигать, если в модель подставить наилучшее значение факторов Х_i.

Наихудшее значение результат Y будет достигать, если в уравнение связи подставить самые “неблагоприятные” значения факторов Х_i.

Усредненное значение результат Y будет достигать, если в модель подставить среднее значение факторов.

Такие модели и прогнозы по ним хорошо работают для конкретных предприятий, т.к. можно рассчитать возможные значения результативного показателя при возможных значениях факторных признаков. Составляют, как правило, оптимистические и пессимистические прогнозы.

В экономическом анализе часто возникает необходимость сопоставить эффективность работы предприятий по многим факторам. При этом приходится учитывать, что предприятия находятся в различных экономических условиях, обладают различными ресурсами и т.д. В этих случаях исходную информацию необходимо привести к какому-либо сопоставимому виду. Таким «видом» является стандартизированный вид. А далее используются методы многомерного сопоставления или кластерный анализ.

В курсе математической статистики в разделе «Выборочный метод и законы распределения случайной величины» устанавливается зависимость между индивидуальными значениями показателя и его средним квадратичным отклонением. Введем обозначения новых стандартизированных переменных, которые отражают долю отклонения индивидуального значения переменной от среднего значения относительно среднеквадратического отклонения:

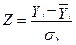
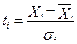(6.60)

где Z_i – стандартизированная результативная переменная.

Значения t_i являются новыми факторными переменными в нашей многофакторной модели, которая называется стандартизированной моделью и выглядит следующим образом:

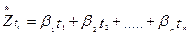(6.61)

где стандартизированными коэффициентами регрессии являются β – коэффициенты. В стандартизированном уравнении нет свободного члена.

Стандартизированное уравнение регрессии может быть найдено (построено) несколькими способами:

1) Первый способ заключается в том, чтобы, не находя значений стандартизированных переменных, рассчитать значения β–коэффициентов по известной нам формуле (6.54) . И затем записать уравнение вида (6.61)

2) Второй способ заключается в том, чтобы, используя исходную базу данных значений всех переменных (результативного и факторных признаков), по формулам (6.60) построить таблицу стандартизированных переменных

Таблица 6.5. Стандартизированные переменные

№ п/п				...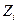
N

Используя значения стандартизированных переменных, можно построить и решить следующую систему линейных уравнений относительно переменных t_i:

(6.62)

Эта система на один параметр в уравнении меньше, чем система (6.43).

Значения переменных таблицы 6.5 могут быть использованы для многомерного или кластерного анализа, которые в данном курсе не рассматриваются.

3) Третий способ заключается в использовании матрицы парных коэффициентов корреляции для нахождения значений β-коэффициентов.

В математической статистике доказывается, что r_ij=r_ji и r_ij=(1/N)*Σt_it_j. Кроме того, мы уже отмечали, что парный коэффициент корреляции равен β-коэффициенту. Поэтому оказывается возможным использовать для расчетов при построении стандартизированного уравнения матрицу парных коэффициентов корреляции.

(6.63)

β- коэффициенты находим по формулам Крамера или методом Гаусса или другим способом.

(6.64)

где Δ_i – частный определитель,

Δ – главный определитель.

Дата добавления: 2014-01-04