Критерий согласия Пирсона

Одной из задач математической статистики является отыскание закона распределения случайной величины. Часто встает вопрос о проверке предположения о нормальном распределении результатов в генеральной совокупности. Для решения этого вопроса используют критерий Пирсона. Для этого сравнивают наблюдаемые частоты и теоретические (вычисленные в предположении нормального распределения) частоты. Обычно эти частоты различаются. Критерий Пирсона определяет, случайны ли расхождения наблюдаемых и теоретических (выравнивающих) частот или эти расхождения являются следствием неправильности гипотезы.

Этапы проверки гипотезы:

1. Выдвигаем нулевую гипотезу:

H₀: результаты в генеральной совокупности распределены нормально.

2. Определяем выравнивающие частоты :

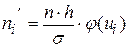, где

n - объем выборки,

h - величина интервала (разность между двумя соседними вариантами),

, - (значение функции см. в таблице, учитывая, что - четная функция).

Вычисления выравнивающих частот оформляется в виде таблицы:

i	xi	ni		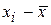	j(ui)

3. Определяем расчетное значение критерия c₀²:

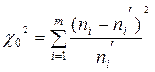, где m – число различных вариант выборки.

Вычисления также представим в виде таблицы:

i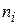

4. Определяем число степеней свободы n:

n = m-3, где m – число различных вариант выборки.

Определение Под числом степеней свободы понимают разность между числом измеряемых значений и числом линейных связей между ними.

5. Находим критическое значение критерия согласия c²:

По заданному уровню значимости 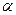и числу степеней свободы n по таблице находим c²(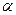; n).

6. Проверка гипотезы: сравниваем расчетное значение c₀² критерия с табличным c².

Если c₀² > c², то гипотеза отвергается на уровне значимости .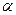

Если c₀² ≤ c², то гипотеза принимается на уровне значимости .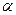

Дата добавления: 2014-01-04