Основные термины. Изучение любого физического процесса связано с установлением зависимости между величинами, характеризующими данный процесс

Дп

ИЯТ

Дг

Однозначности

Изучение любого физического процесса связано с установлением зависимости между величинами, характеризующими данный процесс. Для сложных процессов, к которым относится передача теплоты теплопроводностью, при установлении зависимости между величинами удобно воспользоваться методами математической физики, которая рассматривает протекание процесса в элементарном объеме вещества в течение бесконечно малого отрезка времени.

При выводе дифференциального уравнения теплопроводности пренебрегают изменением некоторых величин и принимают следующие допущения:

• коэффициент теплопроводности X = сопзг, теплоемкость тела С = сопзт, плотность тела/з = сопз1;

• внутренние источники теплоты отсутствуют;

• тело однородно и изотропно;

• соблюдается закон сохранения энергии: разность между количеством теплоты, вошедшим в элементарный объем за время дх и вышедшим из него за это же время, расходуется на изменение внутренней энергии рассматриваемого объема.

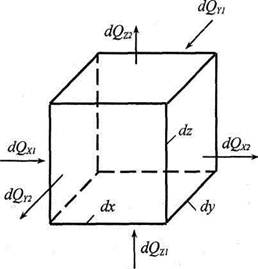
Выделим в теле элементарный параллелепипед с ребрами (Ьс, йу, йг (см. рис. 2.7). Температуры его граней различны, поэтому через них будет проходить теплота в направлении осей X, У, 2.

V

Через площадку дхйу за время ск, согласно закону Фурье, проходит следующее

количество теплоты:

с/<9₂1 - -Мхйуйх

(2.7)

м

^>-

X

Рис. 2.7. Элементарный параллелепипед

Через противоположную грань на расстоянии дг отводится количество теплоты, определяемое из выражения:

&22 = ~Лахдуа'х —

дг

(* /

дг,

(2.8)

(& А - д1, ■ ■..

где г +— дг - температура второй грани; — аг - изменение температуры в направлении

\ дг) дг

оси Ъ.

Уравнение (2.8) можно записать как

Ы

4(2x2 = -^дхдудх —- Ыхдудгдх дг

#1

дг²

(2.9)

Приращение внутренней энергии в параллелепипеде в направлении оси Сбудет равно:

^Яг ⁼ &21 ~ &22 ~ МхфусЬдх

дг²

(2.10)

Для осей X и У приращение внутренней энергии запишется аналогично:

д²{

&Х ~ &Х\ ~ &Х2 = ХШуШх -------- ~,

д²(

дх²

„2

ду

&у - &п ~ ^Яг2 - Адхфдгдт

(2.11) (2.12)

Полное приращение энергии в выделенном объеме равно

⁽ д²1 д²{ д²^

а⁷Я = а*0,х + &У + <^Яг = ^дхдудгдх

дх* ду* дг'

С другой стороны, согласно закону сохранения энергии, можно записать:

АО. = ахаусЬ ■ р С — дх, дт ■

(2.13)

(2.14)

Ы

где дхдудг - объем параллелепипеда; р - плотность тела; С - теплоемкость; — 4т

дг изменение температуры во времени.

Левые и правые части уравнений (2.13) и (2.14) равны, поэтому

Лдхдудгдх

¹' д²1 д²1 д²^

■ + •

■ + •

дх* ду* дг'

= дхдудг • р • С — дх

дх

(2.15)

дх~ Ср

Я (д²1 д²{ д²^

₂+-у + - ₂ дх ду дг)

(2.16)

Уравнение (2.16) называется дифференциальным уравнением теплопроводности, или дифференциальным уравнением Фурье для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты. Это уравнение устанавливает связь между пространственными и временными изменениями температуры в любой точке поля и является основным при изучении теплопроводности.

с

Для упрощения записи уравнения (2.16) вводят следующие обозначения:

Я — = а ~ коэффициент температуропроводности;

д^

д²1

д²1

Ср

+

= V²/ - оператор Лапласа.

сЬГ ду^л дг'

Коэффициент температуропроводности а, м²/с, характеризует скорость изменен температуры и является мерой теплоинерционных свойств тела, ч

Таким образом, уравнение (2.16) можно записать в более компактном виде

I

I

Ы_ дх

(2.17)

I

= аУ²(.

Дифференциальное уравнение теплопроводности с источниками теплоты внутри тел: будет иметь вид

дЧ д²1^Л

+

+

^: + -

(2.18)

\

д²1

дг

Ср

дг'

= а

г

\т ду'

где ау - количество теплоты, вьщеляемой в единице объема вещества в единицу времени,"!
Вт/м\ ]

I

Дифференциальное уравнение (2,16) описывает явление теплйпроводности в самом общем виде, т. е. описывает целый класс явлений. Для того чтобы из этого класса вьщелить "1 конкретньш процесс и дать его полное математическое описание, к дифференциальному^] уравнению необходимо присоединить математическое описание частных особенностей процесса. Эти частные особенности называются условиями однозначности, или краевыми условиями.

Условия однозначности включают:

1. Геометрические условия - задают форму и линейные размеры тела, в котором протекает процесс. ■»!

2. Физические условия - задают физические параметры тела (Я, С, р и пр.), также может быть задан закон распространения внутренних источников теплоты.

3. Начальные условия (для нестационарных процессов) - задают закон распределения температуры внутри тела в начальный момент времени:

'«о =/(*»**) •

При равномерном распределении температуры т = 0, поэтому начальные условия упрощаются (= (₀~ сот(.

4. Граничные условия - задают распределение физических параметров на поверхности тела для каждого момента времени.

Граничные условия бывают I, II и III рода. Граничные условия I рода задают распределение температуры на поверхности тела для каждого момента времени:

1_п=/(х,у,2,%), (2.20)

где /„ - температура поверхности тела.

Граничные условия II рода задают значение теплового потока для каждой точки поверхности тела и любого момента времени:

где д„ - плотность теплового потока на поверхности тела.

(2.21)

В простейшем случае плотность теплового потока по поверхности и во времени остается постоянной д = д₀ = сопз{, такой случай теплообмена имеет место при нагреве металлических изделий в высокотемпературных печах.

Граничные условия Ш рода задают температуру окружающей среды (_ж и закон теплообмена между поверхностью тела и окружающей средой.

Процесс теплообмена между поверхностью тела и окружающей средой называется теплоотдачей. Теплоотдача является очень сложным процессом и зависит от большого количества параметров. Подробнее вопрос о теплоотдаче рассмотрен в теме 2.3.

Граничные условия III рода можно записать в виде

-Т('_с-и> (²-²²>

'аЛ ₌__,

' С * Ж /

Я

где

(дЛ _ - температурный градиент на поверхности тела, м/°С; (_с - температура

\дп)_с поверхности тела, °С; а - коэффициент теплоотдачи, Вт/(м²-°С).

Таким образом, решение дифференциального уравнения теплопроводности при заданных условиях однозначности позволяет определить температурное поле во всем объеме тела для любого момента времени, т. е. найти функцию I -/(х, у, г, х).

Теплообмен, массообмен, теплопроводность, конвекция, излучение.

Температурное поле, стационарное и нестационарное температурное поле.

Изотермическая поверхность.

Температурный градиент, температурный напор.

Количество теплоты, тепловой поток, плотность теплового потока.

Коэффициент теплопроводности.

Условия однозначности.

Дата добавления: 2014-01-04