
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 4. Расчет переходных процессов в разветвленных цепях, интеграл Дюамеля
|
|
|
|
Цель лекции: усвоить расчет переходных процессов в разветвленных цепях классическим методом и при включении цепи на напряжение произвольной формы.
4.1. Расчет переходных процессов в разветвленных цепях классическим методом
Задача решается с помощью уравнений, составленных по законам Кирхгофа для мгновенных значений токов и напряжений, которые в последующем и подлежат определению.
Для простоты изложения рассмотрим порядок расчета токов  в ветвях разветвленных цепей, который заключается в следующем:
в ветвях разветвленных цепей, который заключается в следующем:
- находим принужденные составляющие тока 
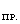 после коммутации;
после коммутации;
- составляем уравнения входного сопротивления Z(p) (в цепи с источником ЭДС) или входной проводимости Y(p) (в цепи с источником тока) для послекоммутационного режима и приравниваем нулю. При этом реактивные сопротивления должны представляться в операторной форме ( или
или  );
);
- после преобразования получаем характеристическое уравнение, куда
подставляем значения заданных параметров, и находим корни 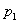 и
и 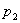 , которые определяют вид свободных составляющих
, которые определяют вид свободных составляющих  (
(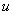
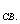 ). Если корни вещественные, отрицательные и
). Если корни вещественные, отрицательные и 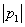 <
<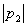 , то для записи свободных составляющих пользуемся уравнением типа (3.4), если
, то для записи свободных составляющих пользуемся уравнением типа (3.4), если 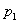 =
= 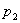 - (3.6), если корни комплексно-сопряженные (
- (3.6), если корни комплексно-сопряженные (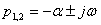 ), то
), то
 , (4.1)
, (4.1)
где 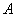 и
и  - постоянные интегрирования;
- постоянные интегрирования;
- записываем уравнение тока в общем виде:
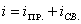 =
= 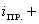
 ; (4.2)
; (4.2)
- для расчета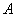 и
и  необходимо еще одно уравнение, для чего возьмем
необходимо еще одно уравнение, для чего возьмем
первую производную тока  по времени
по времени 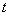 . Тогда для цепи постоянного тока
. Тогда для цепи постоянного тока
 ; (4.3)
; (4.3)
- записываем уравнения тока и его производной при 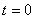
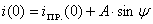 ,
,
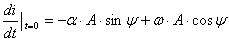 ; (4.4)
; (4.4)
- по законам коммутации и уравнениям Кирхгофа для цепи после комму-
тации при 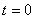 определяем начальные условия
определяем начальные условия 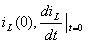 , после чего из (4.4) - постоянные интегрирования
, после чего из (4.4) - постоянные интегрирования и
и  ;
;
- подставив значения и
и  в (4.2), находим закон изменения тока во времени
в (4.2), находим закон изменения тока во времени
 в конкретной ветви схемы.
в конкретной ветви схемы.
Методика расчета напряжений 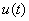 аналогична вышеизложенному.
аналогична вышеизложенному.
Рассмотрим в качестве примера цепь рисунка 4.1.
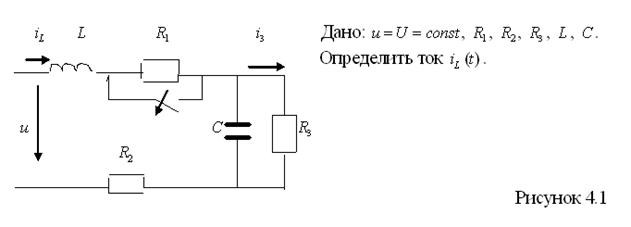
Рассчитываем принужденную составляющую тока 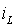
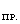
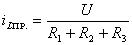 .
.
Составляем уравнение входного сопротивление цепи после коммутации и приравниваем его нулю 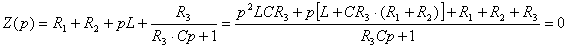 .
.
После преобразования  получаем характеристическое уравнение
получаем характеристическое уравнение
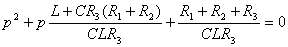 . (4.5)
. (4.5)
Пусть в результате подстановки заданных параметров в (4.5) и его решения корни 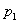 и
и 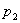 получились комплексно-сопряженными. Тогда свободной составляющей тока
получились комплексно-сопряженными. Тогда свободной составляющей тока 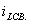 соответствует уравнение (4.1).
соответствует уравнение (4.1).
Записываем уравнение искомого тока в общем виде
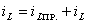
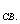 =
=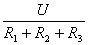
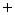
 (4.6) и берем первую производную
(4.6) и берем первую производную 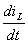 , которая идентична (4.3).
, которая идентична (4.3).
При 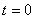 имеем следующее
имеем следующее
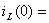
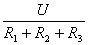
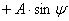 , (4.7)
, (4.7)
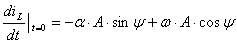 . (4.8)
. (4.8)
По законам коммутации определяем начальные значения тока 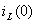 и напряжения на конденсаторе
и напряжения на конденсаторе 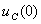
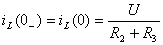 , (4.9)
, (4.9)
 . (4.10)
. (4.10)
Составляем уравнения по второму закону Кирхгофа при 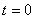
- для внешнего контура
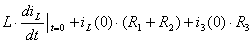
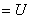 ; (4.11)
; (4.11)
- для контура 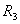 -
- 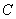

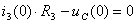 .
.
Находим ток 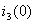
 , т.е.
, т.е.  .
.
С учетом последнего равенства из (4.11) находим 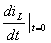
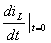
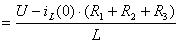 . (4.12)
. (4.12)
Из уравнения (4.7) следует
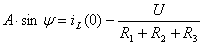 . (4.13)
. (4.13)
Поделив правую и левую части (4.8) на 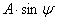 , получим:
, получим:
 ,
,
откуда легко рассчитать 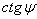 , а после - значение
, а после - значение  .
.
Наконец, из (4.13) находим постоянную интегрирования 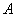 .
.
Подставив в (4.6) числовые значения, получим итоговое выражение 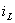
 .
.
4.2 Включение цепи на напряжение произвольной формы
При включении любой цепи на постоянное напряжение 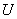 ток в этой цепи во время переходного процесса можно записать в следующем виде
ток в этой цепи во время переходного процесса можно записать в следующем виде
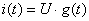 , (4.14)
, (4.14)
где 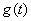 – переходная проводимость цепи. Она зависит от времени и от параметров цепи, но не зависит от величины
– переходная проводимость цепи. Она зависит от времени и от параметров цепи, но не зависит от величины 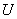 .
.
Наглядное представление о g(t) можно получить, приняв 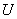 = 1 В.
= 1 В.
Следовательно, 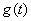 равняется току переходного процесса при включении цепи на постоянное напряжение, равное 1 В.
равняется току переходного процесса при включении цепи на постоянное напряжение, равное 1 В.
Переходную проводимость можно определить для каждой заданной цепи
или классическим методом, или операторным, который будет рассмотрен позже. Например, ток при включении цепи  на постоянное напряжение (см. рисунок 1.1) получился равным
на постоянное напряжение (см. рисунок 1.1) получился равным 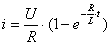 . Следовательно, переход-
. Следовательно, переход-
ная проводимость 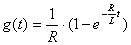 . Отметим, что если цепь включается под напряжение в момент времени
. Отметим, что если цепь включается под напряжение в момент времени  > 0, то
> 0, то  . (4.15)
. (4.15)
При этом 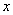 является моментом начала переходного процесса, а начальные условия ставятся для
является моментом начала переходного процесса, а начальные условия ставятся для  .
.
Покажем, что, зная переходную проводимость цепи, можно определить ток в этой цепи при включении ее к источнику любого непрерывно меняющегося во времени напряжения 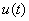 . Пусть
. Пусть 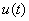 имеет форму, показанную на рисунке 4.2 и требуется, зная
имеет форму, показанную на рисунке 4.2 и требуется, зная 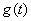 , найти ток
, найти ток  .
.

(если ветвь падающая).
Частичный ток от  равен
равен  , а частичный ток от
, а частичный ток от 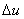 , включенного в некоторый момент
, включенного в некоторый момент  , будет
, будет 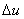
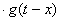 .
.
Проведем в точке 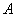 касательную к кривой
касательную к кривой 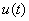 . Тангенс угла ее наклона к оси абсцисс равен производной функции
. Тангенс угла ее наклона к оси абсцисс равен производной функции 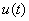 в данной точке, т.е.
в данной точке, т.е. 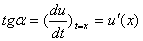 . С учетом того, что
. С учетом того, что  , частичный ток от
, частичный ток от
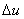 будет равен
будет равен 
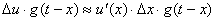 . (4.16)
. (4.16)
Переходя к бесконечно малым интервалам  и суммируя все частичные токи, получим
и суммируя все частичные токи, получим
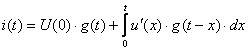 . (4.17)
. (4.17)
Выражение (4.17) – интеграл Дюамеля.
Наряду с указанной существует еще 5 форм записи этого интеграла
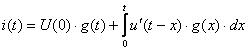 ,
,  ,
,
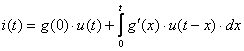
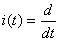
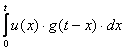 ,
,  . (4.18)
. (4.18)
Из всех форм записи чаще пользуются одной из первых четырех - той, у которой при решении конкретной задачи подынтегральное выражение будет проще.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2074; Нарушение авторских прав?; Мы поможем в написании вашей работы!