
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пусть сопротивление приемника, включенного на выходе линии, равно ее
|
|
|
|
Лекция 10. Однородная линия при различных режимах работы, линия без потерь
Цель лекции: познакомить с режимами согласованной нагрузки, холостого хода, короткого замыкания, уравнениями длинной линии без потерь.
10.1 Режим согласованной нагрузки
волновому сопротивлению 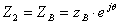 .
.
Тогда напряжение  и уравнения (8.20) примут вид
и уравнения (8.20) примут вид
 ,
,  , (10.1)
, (10.1)
т.е. где бы не производились измерения, в любой точке линии отношение напряжения к току остается неизменным
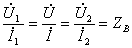 . (10.2)
. (10.2)
Следовательно,  - такое сопротивление, замкнув на которое выходные зажимы линии, будем иметь между входными зажимами точно такое же сопротивление
- такое сопротивление, замкнув на которое выходные зажимы линии, будем иметь между входными зажимами точно такое же сопротивление .
.
Из (8.20) следует, что при 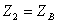 никакого отражения от нагрузки нет
никакого отражения от нагрузки нет  . В линии находится только падающая волна.
. В линии находится только падающая волна.
Рассматриваемый режим называется режимом согласованной нагрузки. Т.к. при этом в линии имеется только одна волна, то можно точнее выяснить смысл коэффициента распространения 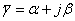 .
.
 , т.е. модуль напряжения изменяется по закону
, т.е. модуль напряжения изменяется по закону 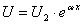 .
.
Если 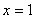 , то
, то 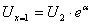 , а коэффициент затухания
, а коэффициент затухания 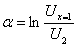 . (10.3)
. (10.3)
Угол между векторами  и
и  равен коэффициенту изменения фазы
равен коэффициенту изменения фазы 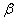 :
:

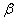 - это угол, на который повернется вектор напряжения или
- это угол, на который повернется вектор напряжения или
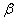 тока на длине x =1 при согласованной нагрузке.
тока на длине x =1 при согласованной нагрузке.
 Так как ток
Так как ток 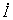 и напряжение
и напряжение  меняются вдоль линии по
меняются вдоль линии по
одному и тому же закону, то и угол сдвига между ними также в любой точке будет одинаков и равен углу волнового сопротивления  . Поэтому мощности на выходе и входе линии определяются соответственно как
. Поэтому мощности на выходе и входе линии определяются соответственно как
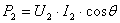 ,
,
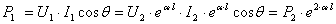 .
.
КПД линии передачи  . (10.4)
. (10.4)
Из (10.4) видно, что КПД линии сильнее зависит от коэффициента затухания  , чем напряжение и ток в отдельности.
, чем напряжение и ток в отдельности.
10.2 Режим холостого хода (Z2=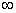 )
)
При холостом ходе ток 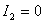 и уравнения длинной линии (9.7) примут вид
и уравнения длинной линии (9.7) примут вид
 ,
, 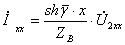 . (10.5)
. (10.5)
Входное сопротивление линии при холостом ходе
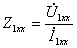
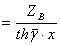 . (10.6)
. (10.6)
Максимум и минимум как 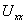 , так и
, так и 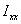 сдвинуты друг относительно друга на четверть длины волны.
сдвинуты друг относительно друга на четверть длины волны.
10.3 Режим короткого замыкания (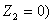
При режиме короткого замыкания напряжение 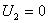 и напряжение и ток в любой точке линии определяется как
и напряжение и ток в любой точке линии определяется как
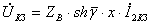 ,
, 
 . (10.7)
. (10.7)
Входное сопротивление линии при коротком замыкании
 (10.8)
(10.8)
Следует отметить, что по данным холостого хода и короткого замыкания можно определить волновое сопротивление и коэффициент распространения волны, т.к. из (10.6) и (10.8) следует, что
 ,
,  . (10.9)
. (10.9)
10.4 Линия без потерь
Если положить 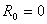 и
и 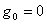 , то получим так называемую линию без потерь. Вообще говоря, это идеализация действительной линии, но в высоко-частотных линиях, применяемых в радиотехнических устройствах,
, то получим так называемую линию без потерь. Вообще говоря, это идеализация действительной линии, но в высоко-частотных линиях, применяемых в радиотехнических устройствах,  <<
<<  и
и  <<
<<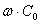 , так что расчеты этих линий ведутся обычно как линий без потерь.
, так что расчеты этих линий ведутся обычно как линий без потерь.
Для такой линии все найденные соотношения упрощаются. Т.к. 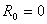 и
и 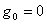 , то продольное сопротивление и поперечная проводимость на единицу длины линии будут
, то продольное сопротивление и поперечная проводимость на единицу длины линии будут
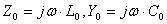 . (10.10)
. (10.10)
Тогда волновое сопротивление линии  , (10.11)
, (10.11)
т.е. оказывается чисто вещественным числом, не зависящим от частоты гене-ратора, питающего линию. Следовательно, токи падающей и отраженной
волн совпадают по фазе со своими напряжениями.
Коэффициент распространения 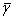 на единицу длины линии оказывается числом мнимым
на единицу длины линии оказывается числом мнимым 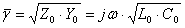 ,
,  (10.12)
(10.12)
т.е. коэффициент затухания 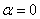 , коэффициент изменения фазы
, коэффициент изменения фазы
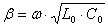 . (10.13)
. (10.13)
Это означает, что величина амплитуд падающей и отраженной волн меня-ться вдоль линии не будет, меняется только фаза этих напряжений и токов.
Фазовая скорость, как и  , не зависит от частоты
, не зависит от частоты  . (10.14)
. (10.14)
Индуктивность и емкость двухпроводной линии (рисунок 10.1):

Рисунок 10.1 Для воздуха  и
и 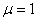 , поэтому
, поэтому  ,
,
т.е. равна скорости света.
Упрощается и уравнение длинной линии. Т.к.  , а
, а  , то
, то
 ,
,
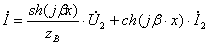 .
.
Но  , а
, а  . Поэтому
. Поэтому
 ,
,
 . (10.15)
. (10.15)
Если принять  , а
, а 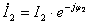 , то мгновенные значения напряжения и тока в любой точке линии будут
, то мгновенные значения напряжения и тока в любой точке линии будут

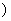 ,
,
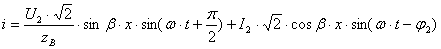 . (10.16)
. (10.16)
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 388; Нарушение авторских прав?; Мы поможем в написании вашей работы!