Лекция 9. Бегущие волны, уравнения длинной линии в гиперболических функциях

Цель лекции: познакомить с расчетом движущихся вдоль линии напряжений и токов, представляемых как результат наложения падающей и отраженной волн, с уравнениями длинной линии в гиперболических функциях при синусоидальном режиме.

9.1 Бегущие волны

Каждое из слагаемых правой части (8.21) можно рассматривать как волну, движущуюся в направлении возрастания или убывания 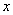и при этом затухающую в направлении движения. Это нетрудно показать, построив их графики изменения вдоль линии.

На рисунке 9.1 представлен график изменения первого слагаемого напряжения 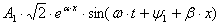в разные моменты времени. Сначала с обеих сторон от оси абсцисс строятся огибающие 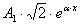, в которые затем вписаны затухающие синусоиды.

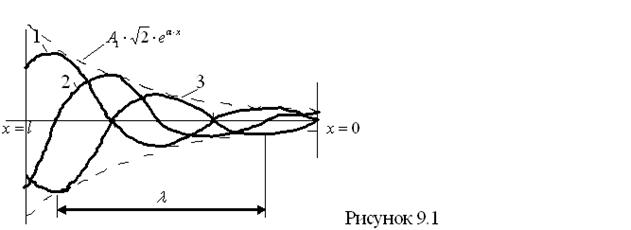
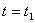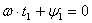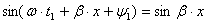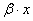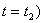
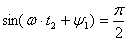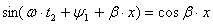Кривая 1 построена для момента времени , когда . Тогда , и, задаваясь значениями равными и т.д., получим различные точки кривой: при они лежат на оси абсцисс, при кривая касается огибающих. Через четверть периода ( и .Задаваясь теми же значениями 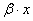строим кривую 2. Кривая 3 построена еще через четверть периода, т.е. при 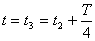, что соответствует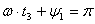и .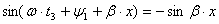

При сравнении этих кривых получается, что волна, постепенно затухая, как бы движется вдоль линии от генератора к нагрузке с некоторой скоростью .

- фазовая скорость, т.е. скорость перемещения точек, фаза которых остается неизменной. Ее можно определить из условия ,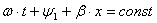

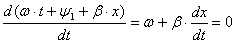, откуда 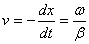. (9.1)

Минус получился потому, что при движении волны от генератора к приемнику у нас 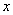уменьшается. Аналогично можно показать, что второе слагаемое представляет собой волну, движущуюся с той же скоростью от приемника к генератору (т.е. в сторону возрастания 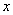), затухая в направлении движения.

Такие волны, движущиеся вдоль линии, называются бегущими. Волна, идущая от генератора к приемнику – падающая и обозначается индексом 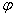. Волна, идущая в обратном направлении – отраженная и обозначается индексом .

Истинную картину распределения напряжения вдоль линии в данный момент времени можно получить, сложив алгебраически ординаты обеих волн для этого момента времени.

Длину волны можно найти как расстояние между точками, фазы колебания которых отличаются на : 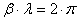, т.е. . (9.2)

Из выражения тока следует, что также можно рассматривать как результат наложения двух затухающих синусоидальных волн, бегущих навстречу друг другу со скоростью .

Условимся о положительных направлениях для падающих и отраженных волн. Обе слагающие напряжения имеют знаки «+», так что естественно выбрать положительные направления и 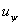совпадающими с положительным направлением действительного напряжения .

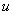Для тока имеются две возможности:

- считать положительное направление 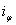совпадающим с положительным

направлением , а положительное направление 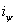- противоположным ему, т.к.

;

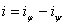- для обеих составляющих взять положительные направления, как для

действительного тока, находить последний как сумму , а минус включить в состав второго слагаемого. Такой выбор удобнее для однотипности записи уравнений, им и будем пользоваться.

Можно записать ,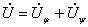

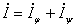, (9.3)

где ;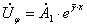

;

;

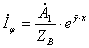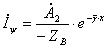. (9.4)

Из (9.4) следует, что ток и напряжение каждой волны связаны между собой законом Ома

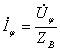, . (9.5)

Физически в линии существуют только действительные токи и напряжения.

9.2 Уравнения длинной линии в гиперболических функциях

Перепишем уравнения (8.20), сгруппировав члены, содержащие напряжение и ток :

,

,

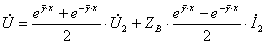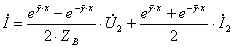но , . (9.6)

С учетом (9.6) уравнения длинной линии при установившемся синусоидальном режиме примут вид

,

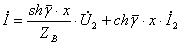. (9.7)

Если требуется найти напряжение и ток на входе линии, т.е. , , 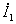то нужно подставить в эти уравнения .

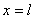(9.7) – уравнения симметричного пассивного четырехполюсника, постоянные которого равны соответственно

, , .

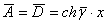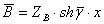Как и всякий симметричный четырехполюсник, линия легко может быть заменена Т-образной или П-образной симметричной схемой замещения, параметры которой можно определить через постоянные четырехполюсника.

Некоторую трудность представляет определение гиперболических функций от комплексного аргумента, которые можно определить или из (9.8)

,

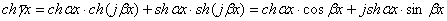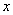, (9.8)

т.к. , ,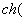

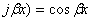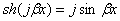или по формулам Эйлера

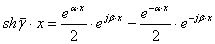, . (9.8а)

Дата добавления: 2014-01-04