Лекция 17. Основные величины, характеризующие электростатическое поле

Электростатическое поле

Цель лекции: изучить основные физические величины, характеризующие электростатическое поле и связь между ними.

17.1.Электрический заряд. Закон Кулона

Поле неподвижных зарядов называют электростатическим. Электриче­ские заряды можно считать бесконечно делимыми и поль­зоваться понятием объемной плотности заряда, поверхностной плотности заряда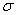, линейной плотности заряда. Безразмерная величина 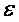называется относительной ди­электрической проницаемостью среды, в которой находятся заряженные тела. Величина 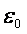называется электрической по­стоянной. Она равна: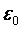=8,854.10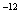Ф/м. Произведение относительной диэлектрической проницае­мости e и электрической постоянной e_о обозначают бук­вой e_а и называют абсолютной диэлектриче­ской проницаемостью. Она, как и электрическая постоянная, измеряется в фарадах на метр.

Если размеры заряженного тела малы по сравнению с расстоянием от него до точек, в которых рассматривается поле, то заряд такого тела называют точечным. Два точечных заряда одного знака оттал­киваются друг от друга. Сила отталкивания определяется законом Кулона

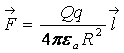, (17.1)

где Q — первый точечный заряд;

q — второй точечный заряд;

R- расстояние между этими точечными зарядами.

Закон Кулона справедлив для точечных заряженных тел. Только в этом случае форма и размеры заряженных тел не влияют на силу взаимодействия. Направление силы взаимодействия F совпа­дает с прямой, соединяющей точечные заряды (рисунок 17.1). Если за­ряды Q и q имеют разные знаки, сила взаимодействия между ними будет силой притяжения, если знаки одинаковые — силой отталкивания. В системе СИ заряд измеряется в кулонах (Кл), сила в ньютонах (Н), расстояние в метрах (м).

17.2 Напряжённость электростатического поляи электрическое смещение

Для описания и измерения электростатического поля пользуются выражением силы отталкивания или притяже­ния, которые испытывает пробное заряженное тело, поме­щенное в это поле. Чем меньше пробный заряд, внесенный в поле, тем меньшая действует на него сила, но отношение их представляет собой конечную величину. Предел отношения силы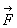, действующей на пробный за­ряд, к этому заряду q, когда он стремится к нулю, называют напряженностью электрического поля

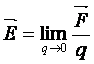. (17.2)

Напряженность электрического поля точечного заряда будет равна

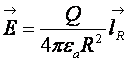. (17.3)

Электростатическое поле можно рассматривать как векторное поле напряженности Е.

Электрическим смещением или электрической индукцией называют век­торную величину 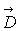, которая в однородных и изотропных средах пропорциональна напряженности электрического поля

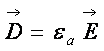. (17.4)

Коэффициент пропорциональности равен абсолютной ди­электрической проницаемости. В системе СИ электрическое смещение измеряется в кулонах на квадратный метр (Кл/м²).

Если поле создается несколькими точечными зарядами, то общая напряженность 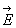электрического поля в любой точке равна геометрической сумме

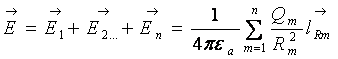, (17.5)

где 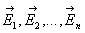— напряженности электрического поля в данной точке, возбужденные зарядами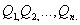

Это положение подтверждается опытом и имеет важное значение. Оно указывает на то, что для электростатического поля применим принцип наложения.

17.3 Потенциальность электростатического поля. Электрический потенциал.

При исследовании полей, чтобы судить о характере поля, необходимо знать, является ли оно вихревым или безвихре­вым. Поле называется безвихревым или потенциальным, если циркуляция век­тора поля вдоль любой замкнутой кри­вой L равна нулю.

Если в электростатическое поле с напряженностью 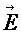внести точечный заряд q, то под действием сил поля заряд начнет перемещаться. Работа, совершенная силами поля при перемещении заряда q из некоторой точки 1 в дру­гую точку 2

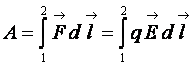. (17.6)

Работа сил поля по замкнутой кривой равна нулю

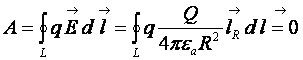. (17.7)

Следовательно, равна нулю и циркуля­ция вектора поля

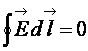. (17.8)

Электростатическое поле безвихревое, потенциальное.

Пользуясь теоремой Стокса, можно преобразовать циркуляции

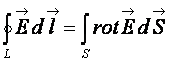. (17.9)

Так как циркуляция вектора напряженности электростатического поля равна нулю, то и ротор его будет равен нулю

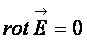. (17.10)

Это соотношение также выражает основное свойство электростатического поля – оно безвихревое. Так как электростатическое поле безвихревое 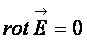, то можно найти такую скалярную функцию 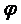, градиент которой, взятый со знаком минус, равен вектору напряженности поля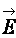

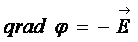. (17.11)

Скалярная функция 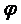называется потенциалом. Потенциал любой точки поля можно определить из выражения

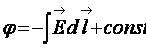. (17.12)

Постоянная интегрирования определяется заданием точки с нулевым потенциалом. Потенциал измеряется в вольтах (В). Разность потенциалов между двумя точками поля а и b равна

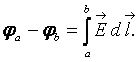(17.13)

Разность потенциалов не зависит от формы пути интегрирования, а зависит только от положения начальной и конечной точек.

Потенциал поля точечного заряда легко найти по формуле

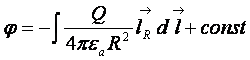. (17.14)

Так как 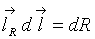, то

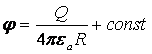. (17.15)

Если принять потенциал равным нулю при R = 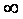, то постоянная интегрирования обратится в нуль.

Потенциал неподвижных объемных, поверхностных и линейных зарядов можно получить методом наложения

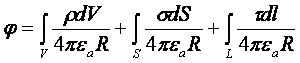. (17.16)

17.4 Графическое изображение электростатического поля

Электростатическое поле графически изображается с по­мощью эквипотенциальных поверхностей и силовых линий. Эквипотенциальные поверх­ности определяются уравнением 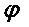= const. Вектор поля во всех точках силовой линии совпадает с касательной. Там, где эквипотенциальные поверхности располагаются ближе, напряженность поля больше. Эквипотенциальные поверхности друг с другом не пересекаются, так как по­тенциал—функция однозначная. След пересечения экви­потенциальной поверхности с плоскостью чертежа назы­вается эквипотенциальной линией. Силовые линии электростатического поля и экви­потенциальные линии взаимно перпендикулярны.

Силовые линии можно изобразить на чертеже следующим образом. Одна из эквипотенциальных поверхностей разби­вается на прямоугольные

площадки. Размер площадок под­бирается таким образом, чтобы поток вектора поля сквозь них имел одно и то же значение. На чертеж наносится по одной силовой линии на каждую площадку, причем так, чтобы эта линия проходила через центр площадки. При таком построении картины поля в тех областях, в которых напряженность больше, силовые линии сгущаются. В эле­ктростатическом поле силовые линии вектора 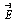— разомкнутые кри­вые. Они начинаются у положительно заряженных поверх­ностей и кончаются у отрицательно заряженных.

Дата добавления: 2014-01-04