Лекция 18. Основные теоремы и уравнения электростатического поля

Цель лекции: изучить основные теоремы и уравнения для электростатического поля.

18.1 Вектор поляризации

Напряженность электростатического поля ,возбужденного зарядом Q, в вакууме и в непроводящем веществе неодинакова. В непроводящей среде напряжен­ность электростатического поля в раз меньше, чем в ва­кууме. Изменение напряженности вызывается поляриза­цией диэлектрика.

Поляризация может происходить различным образом в зависимости от строения молекул диэлектрика. При от­сутствии внешнего электрического поля диэлектрик в це­лом можно считать электрически нейтральным. При нали­чии внешнего поля диэлектрик перестает быть нейтраль­ным, он поляризуется. Заряды, выявившиеся при поля­ризации, связаны с молекулами и могут лишь незначи­тельно перемещаться только внутри этих молекул. Такие заряды называются связанными. В отличие от них заряды, которые можно перенести с одного тела на другое, назы­ваются свободными. Связанные заряды при поляризации создадут свое поле, напряженность которого будет напра­влена противоположно напряженности внешнего поля. По­этому напряженность результирующего поля в диэлект­рике будет меньше, чем напряженность внешнего поля.

Степень поляризации диэлектрика характеризуется векто­ром поляризации , который для однородных и изо­тропных диэлектриков в относительно слабых полях про­порционален напряженности электрического поля

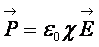. (18.1)

Безразмерная величина называется относительной диэлектрической восприимчивостью.

Поляризованность среды показывает, насколько элек­трическое смещение в данной среде отличается от элект­рического смещения в вакууме

. (18.2)

Следовательно, .

Поляризованность Р, так же как и электрическое сме­щение D, в системе СИ измеряется в кулонах на квадрат­ный метр (Кл/м²).

18.2 Теорема Гаусса в интегральной форме

Теорема Гаусса является одной из фунда­ментальных теорем теории поля. Она гласит: поток вектора электрического смещения сквозь про­извольную замкнутую поверхность S равен алгебраической сумме свободных зарядов Q, расположенных в объеме, огра­ниченном этой поверхностью

. (18.3)

В случае объемного распределения заряда

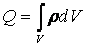. (18.4)

Теорема Гаусса запишется в виде

. (18.5)

Если заряд расположен вне объема, ограниченного замк­нутой поверхностью S, то поток вектора сквозь такую поверхность равен нулю.

Теорема Гаусса широко исполь­зуется при расчете электрических полей.

18.3 Теорема Гаусса в дифференциальной форме

Преобразуем поток вектора электрического смещения по теореме Остроградского

. (18.6)

Так как по теореме Гаусса

,

то

. (18.7)

Объем V был выбран произвольно, и равенство справед­ливо для всех его значений. При таком условии подынтег­ральные выражения должны быть равны и

. (18.8)

Полученное выражение представляет собой дифферен­циальную форму теоремы Гаусса. Оно отмечает то обстоя­тельство, что источники электрического поля находятся только в тех местах, в которых имеются электрические заряды.

Для сред с постоянной диэлектрической проницаемостью можно записать

. (18.9)

Дивергенция вектора величина алгебраическая. Ее знак зависит от знака заряда. Формулы(18.8) и(18.9) справед­ливы и в случае переменного во времени электромагнитного поля.

18.4 Уравнения Пуассона и Лапласа

Электростатическое поле можно рассчитать, пользуясь методом наложения и выра­жениями напряженности и потенциала поля точечного за­ряда или пользуясь интегральной теоремой Гаусса. Оба метода расчета применимы только при расчете полей про­стой конфигурации. В общем случае расчет поля состоит в решении урав­нения Пуассона или Лапласа.

Чтобы получить расчетное уравнение, используем соот­ношения

, .

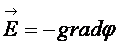Подставив значение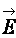, получим

. (18.10)

Дивергенцию градиента принято называть лапласианом и обозначать .Следовательно

. (18.11)

В тех точках поля, в которых нет заряда

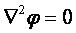. (18.12)

Формула (18.11) носит название уравнения Пуассона. Формула (18.12) — уравнения Лапласа.

Решение может быть записано в виде интеграла

. (18.13)

Введение понятия потенциала облегчает расчет электростатических полей. Он сводится к определению одной скалярной функции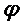,зная которую, можно легко определить напряженность поля из выражения

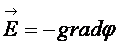. (18.14)

Дата добавления: 2014-01-04