Лекция 20. Электрическое поле постоянного тока

Цель лекции: изучить основные физические величины, характеризующие электрическое поле и связь между ними.

20.1 Ток и плотность тока

Если в проводнике существует электрическое поле, оно вызывает упорядоченное движение зарядов, представляю­щее собой ток проводимости. В металлических проводни­ках ток проводимости определяется движением электронов. Мерой тока служит предел отношения заряда Dq, про­ходящего сквозь заданную поверхность в течение некото­рого времени Dt, к Dt, когда Dt стремится к нулю как к пределу .

Ток — величина скалярная. Если значе­ние тока не зависит от времени, ток называется постоянным. Ток измеряется в амперах (А). Плотностью тока называют векторную величину 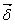, числен­ное значение которой равно пределу отношения тока, про­текающего через некоторую площадку, расположенную нормально к направлению движения зарядов, к площади этой площадки, когда она стремится к нулю как к пре­делу

Направление вектора 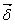выбирается таким образом, чтобы оно совпадало с направлением движения положительных зарядов (или было противоположно направлению движе­ния oтрицательных зарядов).

Ток и плотность тока связаны соотношением

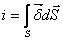. (20.1)

Ток сквозь поверхность S равен потоку вектора плот­ности тока сквозь ту же поверхность. Плотность тока измеряется в амперах, деленных на квадратные метры (А/м²).

20.2 Закон Ома в дифференциальной форме

В изотропном проводнике плотность тока проводимо­сти 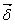пропорциональна напряженности электрического поля Е

. (20.2)

Эта формула представляет собой закон Ома в диффе­ренциальной форме. Коэффициент s называется удельной прово­димостью и измеряется в См/м.

Для того, чтобы в проводнике длительно протекал ток, необходимо наличие электрического поля, силы которого будут перемещать заряды. Такое поле может быть создано и будет поддерживаться процессами не электростатического происхождения (химическими, термоэлектрическими) и носит название стороннего электрического поля. Напряженность стороннего электрического поля обо­значаем Е_стор. Если в проводнике одновременно действуют и электро­статические и сторонние силы, напряженность результи­рующего поля будет равна .

Рассмотрим проводящий контур а— 1 — b— 2 — а (рисунок 20.1).

На уча­стке b — 2 — а действуют сторонние си­лы и на этом участке

.

На участке a — 1 — b сторонних сил нет, поэтому

В замкнутой цепи сумма падений напряжения равна э. д. с.

или.

Разность потенциалов между двумя точками рассматри­ваемого контура меньше э. д. с., действующей в этом кон­туре. Ток на участке a - 1 - b идет от точки а (точки высшего потенциала) к точке b (точке низшего потенциала).

Если бы в цепи не было сторонних сил, то потенциалы точек а и b выровнялись бы и ток прекратился. Наличие сторонних сил заставляет заряды перемещаться от точки b к точке а по пути b — 2 — а и поддерживает потенциалы точек а и b постоянными. Энергия стороннего поля расхо­дуется на тепловые потери как на участке а — 1 — b, так и на участке b — 2 — а. В тех областях проводника, в ко­торых имеются сторонние силы, закон Ома записывается следующим образом

. (20.3)

Закон Ома в дифференциальной форме справедлив как для постоянных, так и для переменных электрических по­лей.

20.3 Закон Джоуля- Ленца в дифференциальной форме

Мощность тепловых потерь в проводнике равна произве­дению тока и напряжения .

Если рассмотреть в проводящей среде элемент объема dV, то мощность, которая тратится в этом объеме на тепловые потери, будет равна

,

откуда . (20.4)

Мощность тепловых потерь в объеме V можно выразить следующим образом . (20.5)

Формула (20.4) является дифференциальной формой за­кона Джоуля—Ленца.

20.4 Первый закон Кирхгофа в дифференциальной форме

Замкнутая поверхность S охватывает узел цепи, к кото­рому подтекают токи I₁ и I₂ и из которого вытекают токи I₃ и I₄ (рисунок 20.2).

Согласно первому закону Кирхгофа I₁ +I₂ =I₃+I_4.

Выразим токи через плотность тока, тогда

Поток вектора плотности тока проводимости сквозь зам­кнутую поверхность равен нулю. Это значит, что заряд, входящий в любой объем, равен заряду, выходящему из него за тот же промежуток времени. Постоянный ток непрерывен. Линии вектора плотности тока 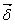замкнуты.

По теореме Остроградского

.

Так как поверхность S, а следовательно, и объем V выбраны произвольно, то можно считать, что

. (20.6)

Плотность тока проводимости не имеет источников. При постоянном токе заряд в любом объеме проводника остается неизменным.

Так как дивергенция плотности тока проводимости равна нулю, то линии вектора 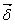замкнуты, поэтому формулу (20.6) называют уравнением непрерывности для постоянного тока.

20.5 Граничные условия

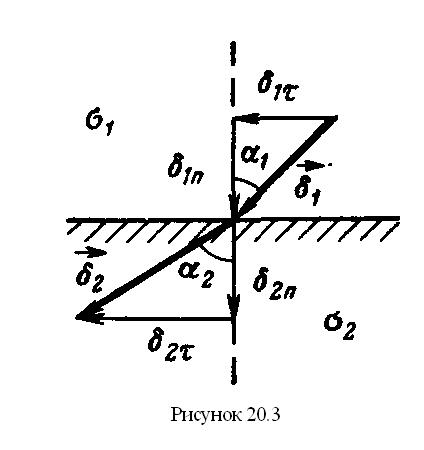
Рассмотрим границу двух проводящих сред, удельные проводимости которых равны σ₁ и σ₂. Граничные условия:

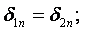а) нормальная составляющая вектора плотности тока на границе двух проводящих сред непрерывна

в) если на границе этих сред нет сторонних сил, то танген­циальные составляющие вектора напряженности электриче­ского поля также должны быть непрерывны у границы

Если векторы 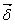и образуют с нормалью к границе угол 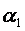в первой среде и угол —во второй (рисунок 20.3), то

Так как

то

20.6 Аналогия между электрическим и электростатическим полями

В области, в которой нет сторонних э. д. с., поле посто­янного тока потенциальное. Потенциал и напряженность поля в такой области связаны соотношением

Так как постоянный ток непрерывен, поле такого тока не имеет источников

.

По закону Ома в дифференциальной форме

В среде с постоянной проводимостью

.

Следовательно

Для определения потенциала поля в рассматриваемой области необходимо решить уравнение Лапласа и учесть гра­ничные условия.

Электростатическое поле в диэлектрике при отсутствии свободных объемных зарядов также описывается уравне­нием Лапласа. Поэтому, если две одинаково ограниченные области: проводящая (без сторонних э. д. с.) и диэлектри­ческая (без свободных объемных зарядов) имеют на гранич­ной поверхности одинаковое распределение потенциала, то внутри каждой из этих областей распределение потенциала будет также одинаковым. Это обстоятельство позволяет пользоваться формулами, полученными при расчете электро­статических полей, в случае поля постоянного тока. При этом емкость необходимо заменить проводимостью, абсолютную диэлектрическую проницаемость — удельной проводимостью.

Например, чтобы определить проводимость изоляции коаксиального кабеля, можно воспользоваться формулой емкости кабеля . Произведя замену, получим .

Дата добавления: 2014-01-04