Лекция 21. Магнитное поле постоянного тока

Цель лекции: изучить основные величины и законы, характеризующие магнитное поле.

21.1Основные величины, характеризующие магнитное поле

Основным свойством неизменного во времени магнитного поля является силовое воздействие его как на движущиеся в нем заряженные тела, так и на неподвижные проводники с электрическим током. Как показывает опыт, магнитное поле обладает определенной направленностью, оно является полем векторным.

Для изучения свойств поля и количественного его опи­сания необходимо ввести физическую величину, которая определила бы интенсивность поля в каждой точке простран­ства. Такой величиной является вектор магнитной индук­ции . Зная , можно установить свойства магнитного поля и вызываемых им явлений.

Если в магнитное поле внести линейный контур с по­стоянным током, то сила, действующая на него, будет равна

(21.1)
где I — ток в контуре L;

dl — элемент длины линейного провода;

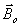— вектор магнитной индукции в пустоте.

Магнитное поле проявилось в виде силы, действующей на контур с током.

Под дей­ствием магнитного поля тока I среда намагнитится. Намагничен­ное вещество создает свое магнит­ное поле с индукцией . Магнитная индукция резуль­тирующего поля . Намагниченное тело при­обретает магнитный момент, который можно рассматривать как результат наличия в среде элементарных контуров с то­ком. Токи эти будем называть микроскопическими в отличие от токов в проводниках, которые назовем макроскопиче­скими. Магнитный момент каждого элементарного контура , где 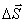— вектор площадки, которая охва­чена током . Плотность магнитных моментов в единице объема намагниченного тела называют вектором намаг­ниченности

Назовем вектором напряженности маг­нитного поля величину

. (21.2)

Тогда . (21.3)

Циркуляция вектора напряженно­сти магнитного поля равна алгебраи­ческой сумме только макроскопиче­ских токов, охваченных контуром ин­тегрирования. Формула (21.3) называется законом полного тока.

Для изотропных сред при слабых магнитных полях век­торы и 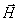пропорциональны . Безразмерный коэффициент c называют магнит­ной восприимчивостью. Скалярная величина c, может быть и положительной и отрицательной. Связь между тремя векторами можно записать и следую­щим образом. Так как

,

то

Безразмерную величину называют отно­сительной магнитной проницаемостью, а произведение— абсолютной магнит­ной проницаемостью. Следовательно,

.

Все вещества обладают магнитными свойствами. Однако у большинства из них магнитные свойства выражены слабо. У диамагнитных веществ относительная магнитная прони­цаемость немного меньше единицы (например, у висмута 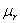= 0,999983), у парамагнитных веществ — немного больше единицы (например, у платины 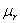= 1,00036). Только у фер­ромагнитных тел 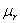значительно больше единицы (сталь, никель), причем она — величина переменная. В первом приближении при расчетах для всех неферромагнитных веществ можно считать 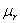= 1. В дальнейшем рассматри­ваются поля только в неферромагнитных средах.

Единицами измерения магнитных векторов в системе СИ являются:

тесла (Тл) — для магнитной индукции В; ампер, деленный на метр (А/м), — для напряженности магнитного поля Н и для намагниченности М.

21.2. Магнитный поток и его непрерывность

Поток вектора магнитной индукции

, (21.4)

называют магнитным потоком. Магнитный по­ток измеряется в веберах (Вб).

Магнитную индукцию можно определить как плотность магнитного потока. Если вектор магнитной индукции перпендикулярен площади S и поле однородно, то Ф = BS.

Установлено, что магнитный поток сквозь замкнутую поверхность всегда равен нулю

. (21.5)

Пользуясь теоремой Остроградского, можно записать

.

Это равенство справедливо для любого объема V. Следовательно

div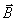= 0. (21.6)

Формула (21.5) выражает принцип непрерывности маг­нитного потока в интегральной форме, формула (21.6) — в дифференциальной. Магнитное поле не имеет истоков. Оно является соленоидальным полем.

Картина магнитного поля графически изображается с помощью линий вектора (магнитных линий). Эти линии либо замкнуты, либо уходят в бесконечность. Положитель­ным направлением их выбирается то направление, куда бу­дет обращен северный полюс магнитной стрелки, внесенной в поле.

В средах с постоянной магнитной проницаемостью div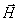=0.

21. 3 Закон полного тока в интегральной и дифференциальной формах

Основным законом, характеризующим свойства магнит­ного поля, является закон полного тока, который устанавли­вает связь между напряженностью магнитного поля и то­ком. Он гласит: циркуляция вектора напряженности маг­нитного поля равна полному микроскопическому току, ко­торый охвачен контуром интегрирования

. (21.7)

Если обозначить плотность полного тока то ток, проходящий через поверхность S, ограниченную кривой L,

.

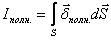Пользуясь теоремой Стокса, можно записать равенство

.

Следовательно

.

Так как это равенство справедливо для всех значений предела интегрирования S, то подынтегральные функции равны между собой

. (21.8)

Полученное уравнение представляет собой дифференци­альную форму записи закона полного тока для независимых от временя полей и носит название первого уравнения Максвелла. Оно указывает на то, что магнитное поле вихре­вое. В вихревом поле работа сил поля по замкнутым кри­вым не всегда равна нулю.

Пользуясь уравнениями

,

можно рассчитать магнитное поле.

21.4 Скалярный и векторный потенциалы магнитного поля

Для области, не занятой токами (вне проводников с то­ками),

m_а= const;

; rot 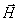=0; div 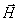=0.

Эти урав­нения аналогичны уравнениям электростатического поля в диэлектрической среде (с e_а = const) при отсутствии объемных зарядов. Следовательно, поле в области, не заня­той токами, можно рассматривать как потенциальное и характеризовать скалярной функцией φ_m, положив

grad j_m = . (21.9)

Величину j_m, называют скалярным магнитным потенциалом.

Если требуется определить напряженность магнитного поля 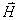по заданной плотности тока 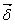, то непосредственное решение первого уравнения Максвелла

может привести к сложным расчетам. В некоторых случаях удобнее вначале определить величину , которая называ­ется векторным потенциалом и связана с ве­личиной 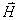соотношением

. (21.10)

Так как написанное соотношение определяет векторный потенциал неоднозначно, надо задать дивергенцию .

Положим div = 0. Если подставить в первое уравне­ние Максвелла вместо напряженности магнитного поля 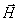равную ей величину то получим

.

Известно, что .

Так как по условию div = 0, то

(21.11) Векторный потенциал магнитного поля определяется по уравнению Пуассона. Решив дифференциальное уравнение, находим . Решение уравнения может быть записано и в виде интеграла

, (21.12)

где R — расстояние от точки, в которой определяется век­торный потенциал, до элементов объема dV, на которые разбит весь объем V;

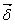— плотность постоянного тока.

Этим решением удобно пользоваться тогда, когда инте­грал легко вычисляется.

Если ток течет по линейному проводнику, то

. (21.13)

Векторный потенциал магнитного поля линейного тока

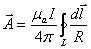. (21.14)

Список литературы

1.К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л. Чечурин. Теоретические основы электротехники. – том 2. – СПб.: Питер, 2003.-463с.

2.Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. Основы теории цепей.- М.: Энергоатомиздат, 1989.-528с.

3.Л.А.Бессонов. Теоретические основы электротехники. – М.: Гардарики, 1999.-638с.

4.Г.В.Бакалов, В.Ф.Дмитриков, Б.Е.Крук. Основы теории цепей.- М.: Радио и связь, 2000.-592с.

5.Сборник задач по теоретическим основам электротехники/Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-543с.

6.Л.А.Бессонов. Теоретические основы электротехники. Электромагнитное поле. – М.: Высшая школа, 1989.-231с.

Сводный план 2007 г., поз. 185

Дата добавления: 2014-01-04