Числовые характеристики случайных величин

Случайная величина

Основные положения математической статистики

Любые контролируемые или измеряемые параметры технической системы изменяются во времени случайным образом, т.е. являются случайными процессами. Фиксируя значения случайного процесса, получают систему случайных величин.

Случайной называют величину, определённой физической размерности, принимающей в результате эксперимента то или иное числовое значение, которое из условий проведения эксперимента нельзя предсказать заранее.

Случайные величины, рассматриваемые далее, будут обозначаться прописными буквами латинского алфавита: X, Y, Z, а их возможные значения строчными – x, y, z. Если случайная величина Х может принять три возможных значения, то они будут обозначены, как, x₁, x₂, x₃.

Для характеристики случайной величины на практике используются числовые характеристики, которые описывают её суммарно.

Наиболее употребительными числовыми характеристиками являются среднеарифметическое значение 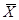, математическое ожидание М(Х), дисперсия D(X) и среднее квадратическое отклонение s(X).

Если среди п событий случайная величина x_i повторяется раз п_i, то среднеарифметическое значение этой величины будет равно:

.

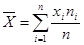Если вместо эмпирических частот использовать их вероятности – р_i, то эта формула даст другую характеристику – математическое ожидание М(Х), т.е для дискретной случайной величины математическое ожидание равно:

.

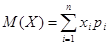Математическое ожидание приближённо равно среднему значению случайной величины, но они различаются. Например, есть 5 измерений одной выборки: х₁=1; х₂=2; х₃=3; х₄=4; х₅=5 с вероятностью р₁=0,1; р₂=0,15; р₃=0,45; р₄=0,3; р₅=0. В этом случае среднее арифметическое будет равно 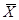=15/5=3,0; а математическое ожидание М(Х)=1×0,1+2×0,15+3×0,45+4×0,3+5×0=2,95.

Для непрерывной случайной величины математическое ожидание может быть рассчитано по формуле: .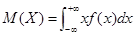

Если систематические погрешности измерений исключены, то истинное значение измеряемой величины равно математическому ожиданию.

Мерой рассеяния (точности измерений) случайной величины относительно её математического ожидания является дисперсия D(X) и среднеквадратическое отклонение s(Х).

Дисперсия D(X) показывает, как рассеяны возможные значения случайной величины вокруг её математического ожидания. Её рассчитывают как математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

Для дискретной случайной величины дисперсия равна .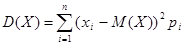

Для непрерывной – .

Например, для рассматриваемого выше примера
D(X)=(1-2,95)²×0,1+(2-2,95)²×0,15+(3-2,95)²×0,45+(4-2,95)²×0,3+(5-2,95)²×0=0,83.

Среднее квадратическое отклонение случайной величины Х – это квадратный корень из дисперсии:

.

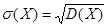Рассмотренные числовые характеристики случайной величины обладают следующими свойствами:

М(с)=с; D(c)=0;

М(сХ)=сМ(Х); D(cX)=c²D(X);

М(а+bX)=a+bM(X); D(a+bX)=b²D(X),

где a, b, c – некоторые константы.

Дата добавления: 2014-01-04