Однофакторная нелинейная регрессии

При составлении математических моделей может оказаться, что предложенное уравнение линейной регрессии неадекватно описывает исследуемый процесс или по виду поля корреляции видно, что линия регрессии криволинейной формы (рис.9). В этом случае порядок уравнения, описывающего процесс, повышается. Для описания процесса, представленного на рис.9, может применяться полином второй степени вида: .

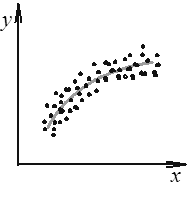
Рис.9 Нелинейная регрессия

Для расчёта коэффициентов уравнения также как и в случае линейной регрессии применяется метод наименьших квадратов. При этом математическая модель подбирается так, чтобы сумма квадратов отклонений фактических значений отклика у от регрессионных 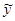была минимальна:

.

Приравнивая к нулю частные производные функции F по коэффициентам b₀, b₁, b₂, получим:

, ,

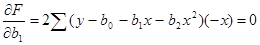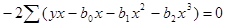,Þ , 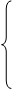Þ

, ,

, ,

,Þ ,

, ,

Введём обозначения: ,

,

,

,

,

,

.

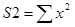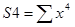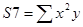Тогда система уравнений будет иметь вид:

,

,

.

Это – система из 3-х уравнений с 3-мя неизвестными b₀, b₁, b₂. Из курса математики известно, что эта система уравнений может быть решена с помощью определителей.

Определитель, составленный из неизвестных коэффициентов уравнений равен:.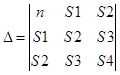

Определитель, полученный заменой в определителе D столбца из коэффициентов при b_0, столбцом свободных членов системы уравнений:

. Аналогично для других неизвестных:

и .

Если определитель D¹0, то решение системы уравнений имеет вид:

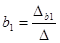, и .

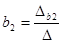Аналогичным образом рассчитываются коэффициентов полиномов любого порядка:

.

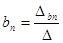Для расчёта коэффициента детерминации r², характеризующего точностные свойства уравнения регрессии, удобно пользоваться формулой:

.

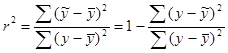Как было отмечено выше, этот коэффициент показывает, какая доля из общего рассеяния экспериментальных значений отклика относительно своего среднего обусловлена регрессионной зависимостью. Коэффициент детерминации находится в пределах 0£ r² £1. Если r²=0, то вариация выходного параметра полностью определяется случайными возмущениями, а влияние фактора х на отклик у не обнаруживается. Если r²=1, то регрессионная кривая проходит через все экспериментальные точки. Однако применение этого критерия при малом числе выборки недостаточно, может даже привести к заблуждению. Поэтому должны рассчитываться все другие критерии, рассмотренные в линейном регрессионном анализе.

Коэффициент корреляции r для нелинейной регрессии является мерой зависимости случайных величин:

.

Чем ближе коэффициент корреляции r к 1, тем теснее связь рассматриваемых признаков.

Оценка адекватности и построение доверительных интервалов проводится по методике, изложенной выше.

Дата добавления: 2014-01-04