Особенности статистического анализа уравнения регрессии активного эксперимента

Уравнение регрессии многофакторного активного эксперимента также как и при обработке результатов пассивного эксперимента подвергается статистическому анализу, в ходе которого определяется адекватность полученной математической модели и статистическая значимость коэффициентов. Адекватность уравнения проверяется по критерию Фишера. Для расчёта F -критерия могут использоваться оценки дисперсий адекватности S²_a и воспроизводимости S²_B:

.

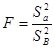Дисперсия адекватности в общем случае может находится по формуле

,

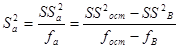где – сумма квадратов адекватности; f_a=N-(k+1) – число степеней свободы дисперсии адекватности; SS²_ocm – остаточная сумма квадратов; SS²_B – сумма квадратов, связанная с дисперсией воспроизводимости; f_ocm – число степеней свободы остаточной дисперсии;

f_B – число степеней свободы дисперсии воспроизводимости.

В зависимости от порядка проведения эксперимента остаточная дисперсия и воспроизводимости рассчитываются по-разному. Выделяют четыре характерных случая.

1) В каждой строке матрицы планирования проводится разное количество параллельных опытов. Тогда

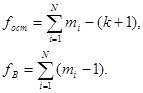
Здесь – арифметическое среднее параллельных опытов.

2) В каждой строке матрицы планирования проводится одинаковое количество параллельных опытов. При таком порядке эксперимента расчёты упрощаются.

3) Параллельные опыты проведены не в каждой строке матрицы планирования, но в центре плана (на базовых уровнях факторов) проведена серия параллельных опытов.

где y_0j – значение выходного параметра в j -том эксперименте для базового уровня факторов, – среднее значение выходного параметра для базового уровня факторов.

4) Параллельные опыты не проводились. В этом случае качество аппроксимации можно оценить, сравнив по критерию Фишера остаточную дисперсию S²_ост и общую S²_О ( рассеяние относительно среднего):

.

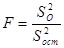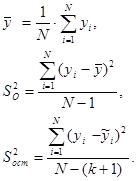
Таким образом, рассчитав оценки дисперсий воспроизводимости и адекватности, вычисляют расчётное значение F -критерия. Сравнивают его с табличным значением F_табл(α, f1, f2) для заданного уровня значимости a, степени свободы дисперсии числителя f1 и степени свободы дисперсии знаменателя f2.

Приближённое уравнение является адекватным при выполнении условия
F ≤F_табл(α, f1, f2) и реализации экспериментов в порядке 1…3 ().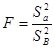

Для случая 4, когда 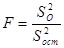, должно выполняться условие F > F_табл(α, f1, f2).

Получив адекватное уравнение приближенной регрессии, приступают к проверке значимости оценок коэффициентов регрессии. Задача данной проверки, также как и при обработке пассивных экспериментов, заключается в установлении статистической значимости или не значимости отличия оценок коэффициентов регрессии от нуля. В результате этого выявляется, обусловлено ли отличие b_i от нуля только случайным влиянием помехи ε (шума эксперимента) или же это отличие не случайно и вызвано тем, что в истинной регрессионной модели присутствует соответствующий коэффициент регрессии, отличный от нуля.

Оценка значимости коэффициентов производится по t- критерию Стьюдента, расчётное значение которого равно:

где –среднее квадратическое отклонение коэффициента b_i.

Ранее отмечалось, что для активного эксперимента все коэффициенты уравнения приближённой регрессии определяются с одинаковой точностью. Поэтому

,

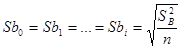где п – общее количество опытов. Дисперсия воспроизводимости рассчитывается в зависимости от условий проведения активного эксперимента.

Расчётные значения t- критериев сравниваются с табличным, t_табл(α, t1), взятым для уровня значимости α, и числа степеней свободы t1=f_В. Коэффициенты b_i считаются статистически значимыми, если выполняется условие t< t_табл(a, t1) (здесь по-другому вычисляется t- критерий по сравнению с ранее рассмотренным вариантом для пассивного эксперимента). В противном случае – коэффициенты являются незначимыми и могут быть исключены из уравнения. При активном эксперименте исключение из уравнения регрессии любого числа незначимых коэффициентов никак не отражается на оставшихся, следовательно, никаких дополнительных перерасчетов делать не нужно.

После исключения всех незначимых коэффициентов следует вновь проверить адекватность уравнения приближенной регрессии и, если оно осталось адекватным, можно приступить к его интерпретации.

Примечание. Иногда в процессе исследований встречается случай, когда проверка адекватности полученного уравнения приближенной регрессии становится невозможной. Как правило, это бывает тогда, когда N вариантов варьирования плана ПФЭ равно числу всех оценок коэффициентов в проверяемом уравнении регрессии. В этом случае знаменатель в зависимостях для расчета дисперсии адекватности обращается в нуль и степеней свободы для проверки гипотезы об адекватности математической модели результатам эксперимента не остается.

В рассматриваемых условиях целесообразно в первую очередь проверить значимость коэффициентов уравнения приближенной регрессии, так как, отбросив незначимые из них, можно получить дополнительные степени свободы для проверки адекватности. Если же все оценки коэффициентов регрессии окажутся значимыми, то есть будут выполняться условия N=k+1, fа=N-(k+1)=0, то в данном случае, целесообразно уменьшить интервалы варьирования входных факторов и вновь провести эксперимент либо сразу перейти к более сложной модели, выбрав полином более высокой степени.

В целом статистический анализ уравнения регрессии при активном эксперименте и выполнении параллельных опытов состоит из приведённых ниже этапов.

1. Расчёт дисперсии адекватности.

2. Расчёт дисперсии воспроизводимости эксперимента (см. п.3.7) :

· Определение среднего арифметического параллельных опытов ;

· Определение дисперсии изменчивости .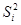

· Проверка однородности дисперсий воспроизводимости по критерию Кохрена.

· Определение дисперсии воспроизводимости параметра оптимизации .

3. Расчёт критерия Фишера

4. Оценка адекватности уравнения регрессии по критерию Фишера.

5. Расчёт t- критериев для коэффициентов приближённого уравнения регрессии.

6. Оценка статистической значимости коэффициентов по критерию Стьюдента.

Дата добавления: 2014-01-04