Пример. Объект исследования – трансформатор тока (ТТ), выполненный на торроидальном сердечнике с немагнитным зазором

Объект исследования – трансформатор тока (ТТ), выполненный на торроидальном сердечнике с немагнитным зазором. Благодаря немагнитному зазору ТТ обладает линейной выходной характеристикой и применяется в качестве датчика тока. Выходной параметр ТТ (у) – напряжение на вторичной обмотке. Независимыми переменными (входными факторами) являются: ток в первичной обмотке I1 (х₁), число витков вторичной обмотки w₂ (х₂), ширина немагнитного зазора d (х₃), сопротивление нагрузки вторичной обмотки трансформатора Rн (х ₄ ). В результате эксперимента необходимо получить математическую модель ТТ, связывающую указанные факторы и отклик и позволяющую получить значение выходного параметра при воздействии совокупности факторов у=f(I1, w₂, d, Rн). Цель – обосновать оптимальные значения параметров ТТ.

Для получения уравнения регрессии применён ПФЭ типа 2⁴, так он даёт максимум информации об объекте при минимуме затрат.

При указанном типе эксперимента переменные устанавливаются на двух уровнях. Предположим, что в результате предварительного изучения ТТ получены интервалы варьирования факторов и пределы их изменения.

Уровни факторов	Факторы
х1 (I1)	х2 (w2)	х3 (d)	х 4 (Rн)
Верхний +1			2,5
Основной 0			1,65
Нижний -1			0,80

.

.

.

.

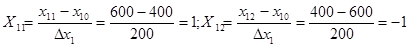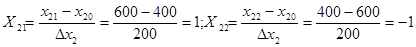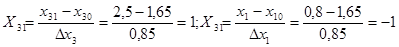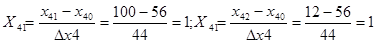Предположим, что проведён эксперимент по приведённому ниже плану.

Оценки изменчивости отклика в дублирующих опытах: .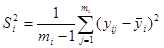

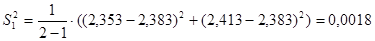; S₂²=0,1004; S₃²=0,0063; S₄²=0,0005; S₅²=0,0125; S₆²=0,0648; S₇²=0,0095; S₈²=0,0631; S₉²=0,0882; S₁₀²=0; S₁₁²=0,0824; S₁₂²=0,2339; S₁₃²=0,0055; S₁₄²=0,0026; S₁₅²=0,045; S₁₆²=0,2586.

Критерий Кохрена равен kкр=0,2586/0,9749=0,2652 < k_кртабл(0,95; 1; 16)=0,45. Дисперсии однородны. Опыты проведены с одинаковой точностью.

В соответствие с формулой 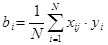определены коэффициенты уравнения регрессии b₀, b₁, … b_34. Получена математическая модель:

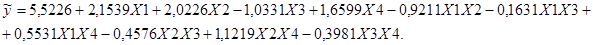Для каждого сочетания факторов рассчитано прогнозируемое значение отклика 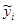. Определены суммы квадратов для подсчёта дисперсии адекватности (для случая, когда число параллельных опытов одинаково): .

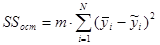1,3452

.

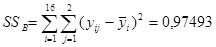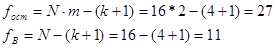
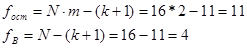
Дисперсия адекватности:

=.

=.

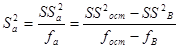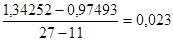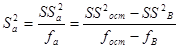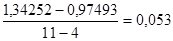Дисперсия воспроизводимости – среднее арифметическое дисперсий изменчивости:

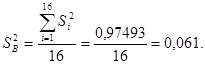
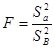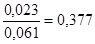= ≤F_табл(0,05, 16, 16)=0,51.

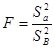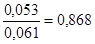= ≤F_табл(0,05, 7, 16)=2,66.

Значимость коэффициентов регрессии по критерию Стьюдента
t_табл(0,05, 16)=1,75.

Средняя квадратическая ошибка коэффициентов равна:

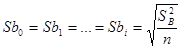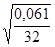==0,044,

Доверительный интервал для коэффициентов:

Dbi=Sbi×tтабл=0,044×1,75=0,077.

Все коэффициенты значимы, так как доверительный интервал меньше этих коэффициентов: Dbi< bi.

Из уравнения видно, что при увеличении переменной Х3 (d) функция отклика (U2) уменьшается. При увеличении других факторов: Х1 (I1), X2 (w1) и X3 (Rн) функция отклика растёт.

Для получения оптимальных соотношений между факторами надо искать экстремальные значения частных производных: .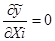

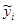
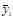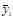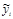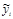№	Х0	Факторы	Отклик		(уi1- )^2	(уi2- )^2	(уi1- )^2	(уi2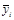- 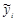)^2	( - )^2
Х1	Х2	Х3	Х4	Х1Х2	Х1Х3	Х1Х4	Х2Х3	Х2Х4	Х3Х4	уi1	yi2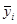
1.	+1	-1	-1	-1	-1	+1	+1	+1	+1	+1	+1	2,353	2,413	2,383	2,297	0,0009	0,0009	0,00314	0,01346	0,0074
2.	+1	+1	-1	-1	-1	-1	-1	-1	+1	+1	+1	4,412	4,86	4,636	3,992	0,05018	0,05018	0,1764	0,75342	0,41474
3.	+1	-1	+1	-1	-1	-1	+1	+1	-1	-1	+1	3,0	3,112	3,056	3,171	0,00314	0,00314	0,02924	0,00348	0,01322
4.	+1	+1	+1	-1	-1	+1	-1	-1	-1	-1	+1	7,931	7,901	7,916	7,831	0,00022	0,00023	0,01	0,0049	0,00722
5.	+1	-1	-1	+1	-1	+1	-1	+1	-1	+1	-1	1,622	1,464	1,543	1,822	0,00624	0,00624	0,04	0,12816	0,07784
6.	+1	+1	-1	+1	-1	-1	+1	-1	-1	+1	-1	3,466	3,106	3,286	3,401	0,0324	0,0324	0,00423	0,08703	0,01322
7.	+1	-1	+1	+1	-1	-1	-1	+1	+1	-1	-1	2,132	2,000	2,086	2,232	0,00212	0,0074	0,01	0,05382	0,02132
8.	+1	+1	+1	+1	-1	+1	+1	-1	+1	-1	-1	6,198	5,843	6,016	5,93	0,03312	0,02993	0,07182	0,00757	0,0074
9.	+1	-1	-1	-1	+1	+1	+1	-1	+1	-1	-1	3,320	2,9	3,110	3,18	0,0441	0,0441	0,0196	0,0784	0,0049
10.	+1	+1	-1	-1	+1	-1	-1	+1	+1	-1	-1	6,175	6,175	6,175	6,16			0,00022	0,00022	0,00022
11.	+1	-1	+1	-1	+1	-1	+1	-1	-1	+1	-1	8,609	8,203	8,406	8,425	0,04121	0,04121	0,03386	0,04928	0,00036
12.	+1	+1	+1	-1	+1	+1	-1	+1	-1	+1	-1	17,108	16,424	16,766	16,807	0,11696	0,11696	0,0906	0,14669	0,00168
13.	+1	-1	-1	+1	+1	+1	-1	-1	-1	-1	+1	2,105	2,0	2,053	2,1	0,0027	0,00281	2,5E-05	0,01	0,00221
14.	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1	4,872	4,8	4,836	4,687	0,0013	0,0013	0,03422	0,01277	0,0222
15.	+1	-1	+1	+1	+1	-1	-1	-1	+1	+1	+1	4,503	4,203	4,353	4,11	0,0225	0,0225	0,15445	0,00865	0,05905
16.		+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	12,142	11,424	11,763	11,903	0,14364	0,11492	0,05712	0,22944	0,0196
S	0,97493	2,32223	1,3452

Матрица ПФЭ типа 2⁴

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Основные понятия теории эксперимента: объект исследования, три вида входных переменных объекта исследования, выходные переменные, план эксперимента, пассивный и активный эксперимент, уровни факторов, матрица плана эксперимента.

2. Основные статистические оценки параметров распределения: математическое ожидание; дисперсия; среднеквадратическое отклонение; исправленная дисперсия.

3. Регрессионный анализ: назначение и сущность.

4. Применение регрессионного анализа для обработки результатов пассивного эксперимента: корреляционная связь между факторами и откликом; поле корреляции; метод наименьших квадратов как математическая основа регрессионного анализа.

5. Оценка тесноты связей между факторами и откликом при регрессионном анализе: коэффициент корреляции; пределы изменения коэффициента корреляции.

6. Оценка тесноты связей между факторами и откликом при регрессионном анализе: коэффициент детерминации; пределы изменения коэффициента детерминации.

7. Оценка достоверности математической модели при регрессионном анализе: средняя ошибка аппроксимации.

8. Оценка адекватности математической модели при регрессионном анализе по F-критерию.

9. Оценка значимости коэффициентов математической модели при регрессионном анализе по t-критерию.

10. Определение доверительных интервалов для коэффициентов регрессионной зависимости.

11. Дисперсионный анализ: назначение, сущность и предпосылки.

12. Формирование матрицы наблюдений для проведения дисперсионного анализа.

13. Проверка однородности дисперсий при дисперсионном анализе по критерию Кохрена?

14. Математическая модель результатов измерений при дисперсионном анализе.

15. Оценка значимости влияния факторов на отклик при дисперсионном анализе.

16. Полный факторный эксперимент (ПФЭ). Матрица планирования при количестве факторов, равных 3.

17. Полный факторный эксперимент (ПФЭ). Расширенная матрица планирования при количестве факторов, равных 2.

18. Дробный факторный эксперимент. Матрица планирования для плана
типа 2^7-3.

19. Применение симплексных планов для решения задачи оптимизации.

20. Способы планирования экспериментов для снижения ошибок при дисперсионном анализе.

21. Параллельные опыты: снижение ошибок и статистическая оценка результатов.

22. Определение коэффициентов регрессии при многофакторном планировании.

23. Интерпретация уравнения регрессии при многофакторном планировании.

24. Оценка адекватности уравнения регрессии при многофакторном планировании.

25. Оценка значимости коэффициентов регрессии при многофакторном планировании.

ИСТОНИКИ ИНФОРМАЦИИ И ЛИТЕРАТУРА

1. Рогов В.А. Методика и практика технических экспериментов: Учеб. пособие для студ.высш.учеб.заведений/ В.А. Рогов, Г.Г. Позняк. – М.: Издательский центр «Академия», 2005. – 283с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов/ В.Е. Гмурман. – М.: Высш. шк., 2005. – 479 с.

3. Кордон М.Я. Введение в научные исследования: [учеб.пособие]/ М.Я. Кордон, В.И. Симакин. – Пенза: Пензен. Гос. ун-т, 2003. -224 с.

Дата добавления: 2014-01-04