
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Учебное пособие
|
|
|
|
для студентов экономических специальностей
Учебное пособие по экономико-математическим моделям и методам предназначено для студентов экономических специальностей. Оно включает в себя теоретический материал, примеры моделирования реальных экономических задач и их методы решения. Приведенные алгоритмы решения задач ориентированы на использование современных информационных технологий.
Для организации самостоятельной работы приводятся варианты индивидуальных заданий с примерами их решения.
Содержание
Содержание. 3
Введение. 4
1. Примеры задач линейного программирования. 5
2. Общая, стандартная и основная задачи линейного программирования 8
3. Геометрическая интерпретация задачи линейного программирования 11
4. Графический метод решения задачи линейного программирования 13
5. Симплекс - метод решения задач линейного программирования 17
6. Двойственные задачи линейного программирования. 32
7. Двойственный симплекс-метод. 42
8. Задача целочисленного линейного программирования. 45
9. Транспортная задача. 51
10. Задачи производственного менеджмента. 69
Задание для самостоятельной работы.. 73
Варианты задач для самостоятельной работы.. 74
Литература. 81
Введение
Линейное программирование является одним из разделов математического программирования – дисциплины, занимающей изучением экстремальных задач и разработкой методов их решения.
В общем виде постановка экстремальной задачи математического программирования состоит в определении наибольшего или наименьшего значения функции  , называемой целевой функцией, при условиях
, называемой целевой функцией, при условиях  , где f и
, где f и  - заданные функции, а
- заданные функции, а  - заданные постоянные величины. При этом ограничения в виде равенств определяют множество допустимых решений, а
- заданные постоянные величины. При этом ограничения в виде равенств определяют множество допустимых решений, а  - называются проектными параметрами.
- называются проектными параметрами.
В зависимости от свойств функции f и  задачи математического программирования делятся на ряд классов задач. Далеко неполная схема задач математического программирования приведена на рис.1.
задачи математического программирования делятся на ряд классов задач. Далеко неполная схема задач математического программирования приведена на рис.1.
Среди них наиболее изученными являются задачи линейного программирования (ЛП), когда все функции f и  - линейные.
- линейные.
Нелинейное программирование – если хотя бы одна из функций f и  - нелинейная.
- нелинейная.
Выпуклое программирование – если отыскивается минимум выпуклой (максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
Целочисленное программирование – если проектные параметры могут принимать лишь целочисленные значения.
Дробно-линейное программирование – если целевая функция f – квадратичная,  - линейные.
- линейные.
Параметрическое программирование – если функции f и  зависят от некоторых параметров.
зависят от некоторых параметров.
Стохастическое программирование – если в функциях f и  содержаться случайные величины.
содержаться случайные величины.
Динамическое программирование – если процесс нахождения решения является многоэтапным.
Рассмотрим задачи, сводящиеся к задачам линейного программирования.

1. Примеры задач линейного программирования
Задача использования ресурсов.
Для производства n видов продукции предприятие использует m видов ресурсов (сырья). Известны нормы затрат ресурсов для производства единицы продукции каждого вида:  - норма затрат i – ого ресурса для производства единицы продукции j – ого вида.
- норма затрат i – ого ресурса для производства единицы продукции j – ого вида.
Ресурсы предприятия имеются в ограниченных объемах 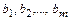 . Предположим, прибыль (доход) от реализации единицы продукции каждого вида величина известная, равная
. Предположим, прибыль (доход) от реализации единицы продукции каждого вида величина известная, равная  .
.
Необходимо при заданных ограничениях на ресурсы определить оптимальный план производства каждого вида продукции, обеспечивающий максимум прибыли.
Обозначим через  план производства каждого вида продукции.
план производства каждого вида продукции.
Найти максимальное значение линейной функции цели (прибыли или дохода) 
при линейных ограничениях
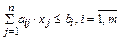 (ограничения на ресурсы);
(ограничения на ресурсы);
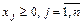 (условие неотрицательности плана производства).
(условие неотрицательности плана производства).
Ниже будет показано, что эта задача нахождения оптимального плана есть стандартная задача линейного программирования.
Замечания:
1. Величины  должны быть определены на основе маркетинговых исследований цен на продукцию и анализа себестоимости единицы продукции.
должны быть определены на основе маркетинговых исследований цен на продукцию и анализа себестоимости единицы продукции.
2. В модели не учтены емкость рынка и объем поступивших заказов. Учет этих факторов рынка можно записать в виде ограничений  , где
, где 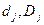 соответственно объем заказов и предельная емкость рынка
соответственно объем заказов и предельная емкость рынка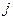 - ой продукции. Это свидетельство взаимосвязанности задач маркетинга и планирования производства.
- ой продукции. Это свидетельство взаимосвязанности задач маркетинга и планирования производства.
3. Оптимальный объем и номенклатура производства могут определяться не только первоначальными запасами ресурсов 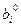 , но и объемом выделенных финансов на производство
, но и объемом выделенных финансов на производство  . Тогда ограничения на ресурсы и финансы запишутся в виде следующих неравенств
. Тогда ограничения на ресурсы и финансы запишутся в виде следующих неравенств
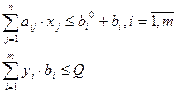
где  - цены на ресурсы, определяемые также из маркетинговых исследований,
- цены на ресурсы, определяемые также из маркетинговых исследований,  - искомые объемы закупаемых ресурсов.
- искомые объемы закупаемых ресурсов.
Таким образом, процесс математического моделирования реальных задач сводится к все большему учету реальных факторов. Эти факторы оказываются связывающими различные бизнес-процессы предприятия. В нашем случае оказались связанными задачи таких бизнес-процессов, как, ПРОИЗВОДСТВО, МАРКЕТИНГ, МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ, СБЫТ, ФИНАНСЫ.
Банковская задача
Свободные средства банка могут быть направлены на выдачу кредитов и приобретение ценных бумаг. Если предположить, что выданные кредиты не являются в полном смысле ликвидными, а ценные бумаги ликвидные, и в то же время кредиты приносят банку больший доход, чем ценные бумаги, то можно поставить задачу определения оптимального плана использования свободных средств.
Предположим, банк имеет свободных средств в размере 120 млн. рублей. Выданные кредиты или обязательства банка по кредитам составляют не менее 30 млн. рублей. Исходя из стратегии (безопасности) банка, не менее чем 40% всех используемых средств должны находиться в ценных бумагах (в ликвидных ресурсах, для выполнения возможных непрогнозируемых обязательств). Определить оптимальный план использования средств, если доход от выданных кредитов составляет в среднем - 20%, а от ценных бумаг – 10%.
Экономико-математическая модель задачи:
Предположим, 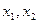 средства банка размещенные соответственно в кредитах и ценных бумагах. Тогда получим следующую задач линейного программирования:
средства банка размещенные соответственно в кредитах и ценных бумагах. Тогда получим следующую задач линейного программирования:
Найти максимум линейной целевой функции – функции дохода

при заданных ограничениях по свободным средствам, по объему выдаваемых кредитов и по стратегии банка

Таким образом, задача определения стратегии банка так же, как и задача использования ресурсов, сводится к стандартной задаче линейного программирования.
2. Общая, стандартная и основная задачи линейного программирования
Определение 1. Общей задачей ЛП называется задача нахождения максимального (минимального) значения линейной целевой функции
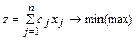 (1) при условиях
(1) при условиях
 ,
,  (2)
(2)
 ,
, 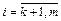 (3)
(3)
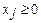 ,
, 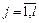 ,
,  (4),
(4),
где 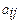 ,
,  ,
,  - заданные постоянные величины и
- заданные постоянные величины и  .
.
Определение.2. Функция Z называется целевой функцией задачи (1 - 4),  - проектными параметрами задачи, а условия (2 - 4) ограничениями данной задачи.
- проектными параметрами задачи, а условия (2 - 4) ограничениями данной задачи.
Определение 3. Стандартной задачей ЛП называется задача нахождения целевой функции (1) при выполнении условий (2), (4), где k=m, l=n, т.е. когда ограничения заданы только в виде неравенств (2), и все проектные параметры удовлетворяют условиям неотрицательности (4), а условия в виде равенств отсутствуют:
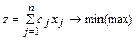
 ,
, 
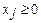 ,
, 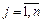 .
.
Определение 4. Канонической (или основной) задачей ЛП называется задача нахождения максимального (минимального) значения функции (1) при выполнении условий (3), (4), где k=0,l=n, m<n,т.е. когда ограничения заданы только в виде равенств (3), и все проектные параметры удовлетворяют условиям неотрицательности (4), а условия в виде неравенств (2) отсутствуют:
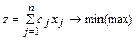
 ,
, 
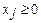 ,
, 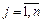 ,
,  .
.
Определение 5. Совокупность значений проектных параметров 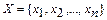 , удовлетворяющих ограничениям задачи (2-4), называется допустимым решением, или планом.
, удовлетворяющих ограничениям задачи (2-4), называется допустимым решением, или планом.
Определение 6. План  , при котором целевая функция (1) принимает свое максимальное (минимальное) значение, называется оптимальным, т.е.
, при котором целевая функция (1) принимает свое максимальное (минимальное) значение, называется оптимальным, т.е.  .
.
Все три формы задачи ЛП эквивалентны, ибо каждая из них с помощью некоторых преобразований может быть переписана в форме другой задачи. При этом необходимо пользоваться следующими правилами:
1. Задачу минимизации функции можно свести к задаче максимизации, и, наоборот, путем замены знаков коэффициентов  на противоположные, поскольку
на противоположные, поскольку  .
.
2. Ограничения-неравенства (2) можно заменить эквивалентными ограничениями-равенствами путем введения дополнительных неотрицательных переменных следующим образом:
Ограничение-неравенство вида  преобразуется в ограничение-равенство
преобразуется в ограничение-равенство 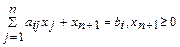 ,
, 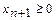 , а ограничение-неравенство вида
, а ограничение-неравенство вида  - в ограничение-равенство
- в ограничение-равенство 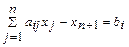 ,
,  .
.
При этом число дополнительных переменных равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный смысл. Так, например, для задачи распределения ресурсов числовое значение дополнительной переменной равно объему неиспользованного соответствующего ресурса. С математической точки зрения основные и дополнительные переменные играют одинаковую роль. Поэтому целесообразно их единообразное обозначение.
4. Каждое ограничение-равенство вида (3) можно записать в виде двух неравенств  .
.
5. Переменная  , неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:
, неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных: 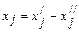 ,
, 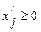 ,
,  .
.
3. Геометрическая интерпретация задачи линейного программирования
Рассмотрим задачу, состоящую в определении максимального значения функции:
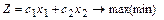 (5) при условиях
(5) при условиях
 ,
,  (6)
(6)
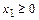 ,
,  (7).
(7).
Эта задача ЛП в стандартной форме с двумя переменными.
Каждое неравенство вида (6), (7) геометрически определяет полуплоскость соответственно с граничными прямыми
 (8).
(8).
При этом вектор  , как градиента функции
, как градиента функции  , указывает ту полуплоскость, которая определяется неравенством
, указывает ту полуплоскость, которая определяется неравенством 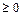 , а вектор
, а вектор 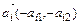 - полуплоскость, определяемую неравенством
- полуплоскость, определяемую неравенством  .
.
Если система неравенств (6), (7) совместна, то область её решений есть множество точек, принадлежащих всем указанным полуплоскостям. Пересечение этих полуплоскостей образует выпуклый многоугольник решений, или область допустимых решений (ОДР).
Таким образом, исходная задача ЛП состоит в нахождении таких точек многоугольника решений, в которых целевая функция Z принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст, и на нем целевая функция ограничена.
Линейная целевая функция достигает точек экстремума только на границе выпуклого многоугольника.
Рассмотрим градиент функции цели  . Это будет вектор
. Это будет вектор  (см. рис.2.), указывающий направление возрастания функции цели. Очевидно, если взять обратное направление, то это будет направлением убывания функции цели. Если построить произвольную прямую
(см. рис.2.), указывающий направление возрастания функции цели. Очевидно, если взять обратное направление, то это будет направлением убывания функции цели. Если построить произвольную прямую 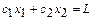 - const, то её движение параллельно самой себе в направлении вектора
- const, то её движение параллельно самой себе в направлении вектора  приведет к возрастанию функции цели. При этом для допустимости решения эта прямая должна иметь хотя бы одну общую точку с многоугольником решений. Два крайних положения этой прямой в ОДР соответствуют наименьшему и наибольшему значениям целевой функции. При этом могут встретиться случаи, изображенные на рис.2-5, когда исходная задача имеет единственное решение (минимальное и максимальное значение) (рис.2), множество решений (координаты любой точки прямой
приведет к возрастанию функции цели. При этом для допустимости решения эта прямая должна иметь хотя бы одну общую точку с многоугольником решений. Два крайних положения этой прямой в ОДР соответствуют наименьшему и наибольшему значениям целевой функции. При этом могут встретиться случаи, изображенные на рис.2-5, когда исходная задача имеет единственное решение (минимальное и максимальное значение) (рис.2), множество решений (координаты любой точки прямой  на рис.3), и решение исходной задачи не существует в силу неограниченности целевой функции (рис.4) или несовместности системы неравенств (6), (7) (рис.5).
на рис.3), и решение исходной задачи не существует в силу неограниченности целевой функции (рис.4) или несовместности системы неравенств (6), (7) (рис.5).
 |
4. Графический метод решения задачи линейного программирования
Графическим методом решается стандартная задача линейного программирования:
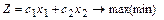
 ,
, 
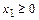 ,
,  .
.
Данный метод основан на приведенной выше геометрической интерпретации задачи ЛП. Нахождение решения задачи ЛП графическим методом имеет следующие этапы:
1. Строят прямые (8), уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений как пересечение всех полуплоскостей
4. Строят начальную прямую (линию уровня целевой функции), проходящую через начало координат  .
.
5. Строят вектор  , представляемый градиент целевой функции (5).
, представляемый градиент целевой функции (5).
6. Движением прямой 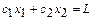 - const параллельно самой себе в направлении вектора
- const параллельно самой себе в направлении вектора  либо находят точки, в которой целевая функция принимает наибольшее (наименьшее) значение, либо устанавливают неограниченность сверху (снизу) целевой функции на множестве планов.
либо находят точки, в которой целевая функция принимает наибольшее (наименьшее) значение, либо устанавливают неограниченность сверху (снизу) целевой функции на множестве планов.
7. Определяют координаты точки максимума (минимума) целевой функции и вычисляют ее значение в этих точках.
Пример. Найти наибольшее и наименьшее значения целевой функции z при заданных ограничениях:

1. Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств:
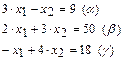
2. Каждое ограничение-неравенство определяет координатную полуплоскость. В зависимости от знака неравенств при помощи двух стрелок укажем требуемые полуплоскости.
3. В результате пересечения всех полуплоскостей находят многоугольник решений (на рисунке обозначен треугольником ABC).
4. Построим начальную прямую (линию уровня целевой функции), проходящую через начало координат  .
.
5. Движением прямой  параллельно самой себе в направлении вектора
параллельно самой себе в направлении вектора  находим два крайних положения. Первое соответствует минимуму целевой функции (точка А), второе - максимуму (точка С).
находим два крайних положения. Первое соответствует минимуму целевой функции (точка А), второе - максимуму (точка С).
Рис.6. Графическая интерпретация задачи линейного программирования

6. Определим координаты точек максимума и минимума целевой функции и вычислим их значения в найденных точках.
- Точка минимума лежит на пересечении прямых  и
и  :
: 
- Точка максимума лежит на пересечении прямых  и
и  :
: 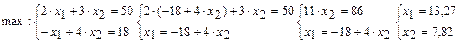 Минимальное значение целевой функции
Минимальное значение целевой функции  .
.
Максимальное значение целевой функции 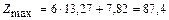 .
.
Вообще, с помощью графического метода может быть решена задача ЛП, система ограничений которой содержит n неизвестных и m линейно-независимых уравнений, если n и m связаны соотношением  .
.
Действительно, пусть поставлена каноническая задача ЛП: найти наибольшее значение
 (12) при условиях
(12) при условиях
 ,
,  (13),
(13),
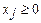 ,
,  (14),
(14),
где все уравнения (13) линейно независимы, и выполняется соотношение  .
.
Используя метод Жордана-Гаусса, производим m исключений, в результате которых система ограничений примет вид:
 ,
, 
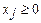 ,
,  . (15)
. (15)
Учитывая неравенства (14), эту систему уравнений можно записать в виде системы неравенств 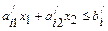 ,
,  ,
,  ,
,  . Исключая
. Исключая  из (12) при помощи уравнений (15), получим
из (12) при помощи уравнений (15), получим  , т.е. задачу вида (5-7).
, т.е. задачу вида (5-7).
5. Симплекс - метод решения задач линейного программирования
Введение.
Предположим, что поставлена стандартная задача ЛП:
 ,
,
 ,
,  , (16)
, (16)
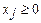 ,
,  .
.
Каждое из условий типа неравенства определяет полупространство, ограниченное гиперплоскостью (плоскостью в k -мерном пространстве). Пересечение соответствующих полупространств образует выпуклый многогранник (область допустимых решений - ОДР), в котором необходимо найти максимум (минимум) целевой функции. Внутри многогранника условий в силу его выпуклости линейная функция z не может достигать максимума (минимума). Её максимум (минимум), если он существует, достигается обязательно в какой-нибудь вершине многогранника или на одном из его граней.
Теоретически задача ЛП проста. Достаточно найти конечное число вершин многогранника и вычислить в них значения целевой функции. Из всех этих значений выбрать то, которое соответствует оптимальному решению.
Однако простой перебор даже при использовании самых современных ЭВМ практически неосуществим из-за чрезвычайно большого числа вершин. Поэтому возникла необходимость применения методов целенаправленного перебора, которые приводят к решению задачи за приемлемое время. Одним из таких методов является симплекс-метод.
Симплексом называется простейший выпуклый многогранник. Решение задачи ЛП симплекс-методом состоит в определении одной из вершин многогранника условий и последовательном переходе от одной вершины к другой, причем каждый такой переход приближает решение к оптимальному. В этом заключается геометрический смысл симплекс-метода.
Рассмотрим каноническую задачу линейного программирования:

 ,
,  ,
,  , (17)
, (17)
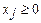 ,
,  .
.
Здесь систему ограничений представляет система m линейно независимых уравнений. Эта система линейных уравнений имеет бесконечное число решений. При этом (n-m) переменных могут принимать произвольные значения (свободные переменные), а остальные m переменных выражаются через них (базисные переменные).
Определение 7. Решение, при котором все свободные переменные равны нулю, называются базисным решением.
Очевидно, что не всякое базисное решение является допустимым, т.е. принадлежит многограннику условий, так как необходимо учесть последние условия неотрицательности всех переменных из (17).
Определение 8. Базисное решение, удовлетворяющее условиям неотрицательности всех переменных, называется допустимым базисным решением, или опорным планом.
Определение 9. Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае, он называется вырожденным.
На каждой грани многогранника условий какая-либо переменная тождественно равна нулю. Например, из (16), (18) видно, что гиперплоскость  , которая, возможно, является одной из сторон многогранника условий, соответствует условию
, которая, возможно, является одной из сторон многогранника условий, соответствует условию 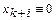 . Поэтому в каждой вершине многогранника условий обращаются в нуль ровно столько переменных, сколько свободных. Таким образом, допустимое решение, соответствующее какой-либо вершине многогранника условий, необходимо искать среди множества базисных решений.
. Поэтому в каждой вершине многогранника условий обращаются в нуль ровно столько переменных, сколько свободных. Таким образом, допустимое решение, соответствующее какой-либо вершине многогранника условий, необходимо искать среди множества базисных решений.
Алгоритм симплекс-метода.
Первоначально задача ЛП записывается в канонической форме (17), и находится произвольное базисное решение. Если решение недопустимое, то проверяется совместность ограничений, и, в случае совместности, из базиса вычеркивается определенная переменная, а вместо неё вводится другая. Тем самым, находится новое базисное решение. Если же базисное решение допустимое (т.е. найден опорный план, соответствующий одной из вершин многогранника условий), то решение проверяется на оптимальность. В случае неоптимальности допустимого базисного решения, устанавливается ограниченность целевой функции, и вновь производится обмен между базисными и свободными переменными, который геометрически означает переход к другой вершине многогранника.
В результате многократного повторения указанного процесса, либо будет получено оптимальное решение, либо будет выявлена противоречивость ограничений (несуществование ОДР), либо будет видно, что целевая функция неограничена.
Алгоритм симплекс-метода представлен при помощи блочных структур на рис.7.

При решении задачи симплекс-методом удобно пользоваться так называемыми симплекс-таблицами. Приведем некоторые пояснения к алгоритму нахождения оптимального решения, основанного на последовательных переходах от одной симплекс-таблицы к другой.
Представление исходных данных задачи в виде симплекс-таблицы (первая симплекс-таблица). Для получения симплекс-таблицы общую или стандартную задачу ЛП необходимо привести в канонический вид и разрешить систему линейных уравнений (например, методом Гаусса-Жордана) относительно выделенных базисных переменных. Далее, следует при помощи выражений для базисных переменных выразить целевую функцию через свободные переменные.
При составлении первой симплекс-таблицы на основе разрешенной системы линейных уравнений, свободные члены записываются без изменения знаков, а коэффициенты при свободных переменных - с противоположными знаками. Предположим для определенности, дана стандартная задача ЛП в виде (16). Введя дополнительные неотрицательные переменные  , получим соответствующую каноническую задачу ЛП:
, получим соответствующую каноническую задачу ЛП:
 ,
,
 ,
,  , (18)
, (18)
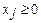 ,
,  .
.
Предполагая, что 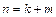 и равенство нулю некоторых
и равенство нулю некоторых  , эту задачу можно записать в виде (17).
, эту задачу можно записать в виде (17).
В данном случае удобно в качестве базисных переменных выбрать  , относительно которых легко решить систему уравнений. Поэтому из (18) следует
, относительно которых легко решить систему уравнений. Поэтому из (18) следует
 ,
,
 ,
,  , (19)
, (19)
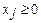 ,
,  , где
, где  ,
,  ,
, 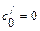 .
.
Из такой записи канонической задачи ЛП составляют симплекс-таблицу (см. Таб.1).
В дальнейшем эта таблица подвергается анализу, и в случае необходимости проводится такое преобразование, когда одна переменная из свободных переходит в базисные, а одна базисная – в свободные.
Таб.1. Составление первой симплекс-таблицы
| Базисные переменные | Свободные члены | Свободные переменные | ||||
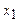
| … | 
| … | 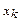
| ||

| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
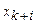
| 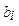
| 
| … | 
| … |  
|
| … | … | … | … | … | … | … |
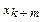
| 
| 
| … | 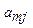
| … | 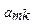
|
| Целевая функция Z | 
| 
| … | 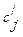
| … | 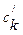
|

Нахождение базисного решения. В базисном решении все свободные переменные равны нулю, и поэтому базисные переменные равны свободным членам (см. (19) и Таб.1):  .
.
Проверка допустимости базисного решения.
Признак 1. (Признак допустимости базисного решения). Решение будет допустимым, если в симплекс-таблице все свободные члены (кроме строки целевой функции) неотрицательные.
Проверка совместности ограничений. Если базисное решение недопустимо, то необходимое проверить совместность ограничений, т.е. наличие ОДР. Геометрическая интерпретация несовместности ограничений показана на рис.5.
Признак 2. (Признак несовместности ограничений). Ограничения несовместны, если в любой строке (кроме строки целевой функции), имеющей отрицательный свободный член, нет ни одного отрицательного элемента. Наличие отрицательного элемента дает возможность произвести такой обмен переменных, когда новая базисная переменная возможно станет неотрицательной.
Если несовместность по изложенному признаку не выявлена, то необходимо произвести преобразование симплекс-таблицы (обмен переменных), цель которого нахождение нового базисного решения.
Проверка оптимальности решения. Если базисное решение допустимое, то решение проверяется на оптимальность с помощью следующего признака.
Признак 3. (Признак оптимальности решения). Целевая функция будет иметь максимальное (минимальное) значение, если в строке целевой функции все элементы, кроме свободного члена, положительные (отрицательные).
Проверка ограниченности целевой функции. Если допустимое базисное решение неоптимальное, то необходимо проверить существование оптимального решения, т.е. ограниченности целевой функции. Геометрическая интерпретация неограниченности целевой функции показана на рис.4.
Признак 4. (Признак ограниченности целевой функции). Целевая функция ограничена сверху (снизу), т.е. существует максимальное (минимальное) значение целевой функции, если на каждой итерации в каждом столбце, не удовлетворяющем признаку оптимальности, есть хотя бы один положительный элемент.
Если не выявлено несуществование оптимального решения по этому признаку, то итерацию необходимо повторить, т.е. преобразованием симплекс-таблицы перейти к новому базисному решению.
Проверка неединственности решения.
Признак 5. (Признак неединственности оптимального решения). Если в строке целевой функции оптимального решения, кроме столбца свободных членов, есть хотя бы один нулевой элемент, то полученное оптимальное решение является неединственным.
Это означает, что есть другой набор значений переменных, при котором целевая функция будет иметь такое же оптимальное значение.
Таким образом, анализ симплекс-таблицы может привести к необходимости её преобразования, переходу к новому базисному решению. Для этого необходимо найти разрешающий элемент.
Нахождение разрешающего элемента. Разрешающий элемент указывает одну свободную и одну базисную переменные, которые следует обменять, чтобы получить новое “улучшенное” базисное решение.
Шаг 1. Нахождение разрешающего столбца.
ü базисное решение недопустимое, ограничения совместны.
В строке, содержащей отрицательный свободный член, выбирается отрицательный элемент. Столбец, в котором находится выбранный элемент, принимается в качестве разрешающего.
ü базисное решение допустимое, неоптимальное.
В качестве разрешающего столбца принимается любой столбец, неудовлетворяющий признаку оптимальности.
Шаг 2. Нахождение разрешающей строки.
Определяются положительные отношения свободных членов к элементам разрешающего столбца  ,
, 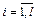 , где l – число строк, в которых
, где l – число строк, в которых 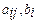 имеют одинаковый знак. В качестве разрешающей, выбирается та строка, для которой найденное значение минимальное, т.е.
имеют одинаковый знак. В качестве разрешающей, выбирается та строка, для которой найденное значение минимальное, т.е.  .
.
Разрешающие строка и столбец в Таб.1 помечены стрелками, разрешающий элемент выделен рамкой.
Замечание. Если выбор разрешающего элемента неоднозначный, то можно выбрать любой из них. Это может несущественно повлиять лишь на количество итераций, но не влияет на оптимальное решение. Обеспечение минимального количества итераций здесь не рассматривается, однако, рекомендуется выбрать наименьший, если элемент отрицательный и наибольший, если выбираемый элемент положительный.
Преобразование симплекс-таблицы. Как уже отмечалось, преобразование симплекс-таблицы заключается в обмене переменных. Предположим, что разрешающий элемент является 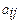 , который выделен рамкой в Таб.1. Тогда базисную переменную
, который выделен рамкой в Таб.1. Тогда базисную переменную  необходимо перевести в свободные, а свободную переменную
необходимо перевести в свободные, а свободную переменную  - в базисные. Переход от одной таблицы к другой выполняется по следующему алгоритму.
- в базисные. Переход от одной таблицы к другой выполняется по следующему алгоритму.
Шаг 1. Ячейка разрешающего элемента заполняется значением 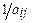 , обратным значению разрешающего элемента.
, обратным значению разрешающего элемента.
Шаг 2. Ячейки разрешающей строки заполняются элементами, стоящими в этих ячейках, деленными на разрешающий элемент, т.е.
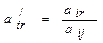 ,
, ,
,
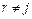 ,
, . (20)
. (20)
Шаг 3. Ячейки разрешающего столбца заполняются элементами, стоящими в этих ячейках, деленными на разрешающий элемент с обратным знаком, т.е.
 ,
, ,
, ,
,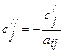 . (21)
. (21)
Шаг 4. Остальные ячейки  ,
,  ,
, 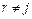 заполняются значениями, стоящими в этих ячейках, минус произведение элементов, стоящих в соответствующем разрешающем столбце и в соответствующей разрешающей строке, деленное на разрешающий элемент, т.е.
заполняются значениями, стоящими в этих ячейках, минус произведение элементов, стоящих в соответствующем разрешающем столбце и в соответствующей разрешающей строке, деленное на разрешающий элемент, т.е.
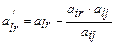 ,
,
 , (22)
, (22)
 ,
,  ,
,
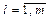 ,
,  ,
, 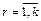 ,
, 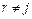 .
.
В силу того, что на шаге 3 значения элементов пересчитанного разрешающего столбца 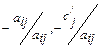 уже определены, то вычисления по формулам (22) можно сократить.
уже определены, то вычисления по формулам (22) можно сократить.
В результате преобразования получим новую симплекс-таблицу (Таб.2).
Таб.2. Преобразование симплекс-таблицы
| Базисные переменные | Свободные члены | Свободные переменные | ||||

| … | 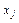
| … | 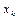
| ||

| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |

| 
| 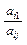
| … | 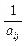
| … | 
|
| … | … | … | … | … | … | … |

| 
| 
| … | 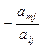
| … | 
|
| Целевая функция Z | 
| 
| … | 
| … | 
|
Пример. Найти наибольшее значение целевой функции z при заданных ограничениях:
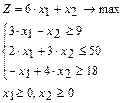
Исходную стандартную задачу линейного программирования (СЗЛП) приведем к каноническому виду (КЗЛП). Для этого введем дополнительные переменные, учитывая знаки неравенств-ограничений. Если ограничение-неравенство имеет знак «≥», то дополнительную переменную вводим со знаком «-», в противном случае – со знаком «+».
|
|



В качестве базисных переменных удобно выбрать  , так как относительно этих переменных легко решить систему линейных уравнений:
, так как относительно этих переменных легко решить систему линейных уравнений:  - базисные переменные;
- базисные переменные;  - свободные переменные.
- свободные переменные.

Составим первую симплекс-таблицу: свободные члены записываем без изменения знаков, а коэффициенты при свободных переменных – с противоположными знаками.
| Базисные переменные | Свободные члены | Свободные переменные | |
| x1 | x2 | ||
| x3 | -9 | -3 | |
| x4 | |||
| x5 | -18 |  -4 -4
| |
| Z | -6 | -1 |

Базисное решение  - недопустимое, т.к. имеются отрицательные элементы (
- недопустимое, т.к. имеются отрицательные элементы ( ). Данная симплекс-таблица соответствует точке начала координат на рис.6. Ограничения совместны, т.к. в строках с отрицательными свободными членами имеются ещё отрицательные элементы. Необходимо найти разрешающий элемент и провести преобразование симплекс-таблицы.
). Данная симплекс-таблица соответствует точке начала координат на рис.6. Ограничения совместны, т.к. в строках с отрицательными свободными членами имеются ещё отрицательные элементы. Необходимо найти разрешающий элемент и провести преобразование симплекс-таблицы.
Найдём разрешающий элемент. Выберем наименьший отрицательный элемент в строках с отрицательными свободными членами. Это -4. Столбец, в котором находится этот элемент (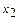 ), принимаем в качестве разрешающего столбца (помечен стрелкой).
), принимаем в качестве разрешающего столбца (помечен стрелкой).
Для нахождения разрешающей строки определяем минимальное положительное отношение свободных членов к элементам разрешающего столбца. Так как  , то в качестве разрешающей строки получаем
, то в качестве разрешающей строки получаем  .
.
Элемент, находящийся на пересечении разрешающих столбца и строки, является разрешающим элементом (выделен рамкой). Он указывает, что базисную переменную  переводим в свободные, а свободную переменную
переводим в свободные, а свободную переменную 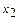 - в базисные.
- в базисные.
Преобразуем симплекс-таблицу, используя правила преобразования:
1. Ячейку разрешающего элемента, равного «-4», заполняем значением, обратным значению разрешающего элемента (-1/4=-0,25).
2. Ячейки разрешающей строки  заполняем элементами, стоящими в этих ячейках, деленными на разрешающий элемент «-4». Например, элемент, находящийся на пересечении столбца свободных членов и строки
заполняем элементами, стоящими в этих ячейках, деленными на разрешающий элемент «-4». Например, элемент, находящийся на пересечении столбца свободных членов и строки  , будет равен
, будет равен  .
.
3. Ячейки разрешающего столбца заполняем элементами, стоящими в этих ячейках, деленными на разрешающий элемент с обратным знаком «4». В частности, элемент, находящийся на пересечении столбца 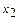 и строки
и строки  , будет равен
, будет равен 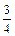 .
.
4. Остальные ячейки заполняем значениями, стоящими в этих ячейках, минус произведение элементов, стоящих в соответствующем разрешающем столбце и в соответствующей разрешающей строке, деленное на разрешающий элемент «-4». Например, элемент, находящийся на пересечении столбца свободных членов и строки  , будет равен
, будет равен  .
.
В результате преобразования симплекс-таблицы получим:
| Базисные переменные | Свободные члены | Свободные переменные | |
| x1 | x5 | ||
| x3 | 
| 
|  
|
| x4 | 
| 
| 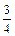
|
| x2 | 
| 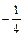
| 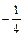
|
| Z | 
| 
| 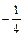
|

Базисное решение 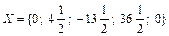 - недопустимое, т.к. есть отрицательный элемент (
- недопустимое, т.к. есть отрицательный элемент (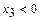 ). Ограничения совместны, т.к. в строке с отрицательным свободным членом имеется ещё отрицательный элемент.
). Ограничения совместны, т.к. в строке с отрицательным свободным членом имеется ещё отрицательный элемент.
В качестве разрешающего столбца выбираем столбец 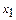 . Вычисляя
. Вычисляя 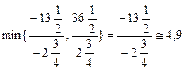 , получаем, что в качестве разрешающей строки следует выбрать
, получаем, что в качестве разрешающей строки следует выбрать  . Базисную переменную
. Базисную переменную  переводим в свободные, а свободную переменную
переводим в свободные, а свободную переменную 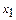 - в базисные.
- в базисные.
В результате преобразования симплекс-таблицы получили следующую таблицу:
| Базисные переменные | Свободные члены | Свободные переменные | |
| x3 | x5 | ||
| x1 | 
| 
| 
|
| x4 |  1 1
| ||
| x2 | 
| 
| 
|
| Z | 
| 
| 
|

Базисное решение 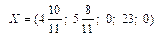 - допустимое, т.к. все свободные члены положительные. Решение оптимальное (минимум целевой функции), поскольку в строке целевой функции, кроме столбца свободных членов, все элементы одного знака (отрицательные). Оптимальное решение единственное, т.к. в строке целевой функции нет нулевых элементов. Данная симплекс-таблица соответствует точке А на рис.6.
- допустимое, т.к. все свободные члены положительные. Решение оптимальное (минимум целевой функции), поскольку в строке целевой функции, кроме столбца свободных членов, все элементы одного знака (отрицательные). Оптимальное решение единственное, т.к. в строке целевой функции нет нулевых элементов. Данная симплекс-таблица соответствует точке А на рис.6.
Но поскольку требуется найти максимальное значение целевой функции, то итерации продолжаются.
В качестве разрешающего столбца можно выбрать любой столбец таблицы, т.к. они оба не удовлетворяют признаку оптимальности (максимуму). Выбираем столбец  . Тогда разрешающей строкой будет строка
. Тогда разрешающей строкой будет строка  , т.к.
, т.к.  .
.
В результате преобразований получим следующую симплекс-таблицу:
Таб.3. Симплекс-таблица оптимального решения
| Базисные переменные | Свободные члены | Свободные переменные | |
| x4 | x5 | ||
| x1 | 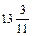
| 
| 
|
| x3 | |||
| x2 | 
| 
| 
|
| Z | 
| 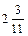
| 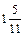
|
Базисное решение  - допустимое, т.к. все свободные члены положительные. Решение оптимальное (максимум целевой функции), поскольку в строке целевой функции все элементы одного знака (положительные). Оптимальное решение единственное, т.к. в строке целевой функции нет нулевых элементов. Данная симплекс-таблица соответствует точке С на рис.6.
- допустимое, т.к. все свободные члены положительные. Решение оптимальное (максимум целевой функции), поскольку в строке целевой функции все элементы одного знака (положительные). Оптимальное решение единственное, т.к. в строке целевой функции нет нулевых элементов. Данная симплекс-таблица соответствует точке С на рис.6.
Таким образом, наибольшее значение  целевая функция имеет при
целевая функция имеет при  .
.
6. Двойственные задачи линейного программирования
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу, называемую двойственной или сопряженной по отношению к исходной или прямой.
1. Симметричная пара взаимно двойственных задач:
Рассматривается стандартная задача линейного программирования (СЗЛП):
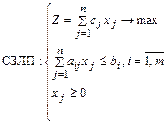
Тогда двойственная ей задача (ДЗЛП) будет иметь вид:

Экономическая интерпретация взаимно двойственных задач.
СЗЛП: Составить такой план продукции  , при котором выручка (прибыль) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющиеся запасы.
, при котором выручка (прибыль) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющиеся запасы.
ДЗЛП: Найти такой набор цен (оценок) ресурсов 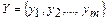 , при которых общие затраты на ресурсы будут минимальными, а созданная стоимость единицы продукции каждого вида будет не менее выручки от реализации единицы продукции. Оценки
, при которых общие затраты на ресурсы будут минимальными, а созданная стоимость единицы продукции каждого вида будет не менее выручки от реализации единицы продукции. Оценки 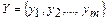 называются учетными или теневыми.
называются учетными или теневыми.
Положительную двойственную оценку имеют лишь те виды ресурсов, которые полностью используются при оптимальном плане производства продукции и увеличить этот доход можно только при увеличении этих ресурсов. Поэтому двойственные оценки определяют дефицитность используемых ресурсов: в оптимальном плане дефицитные ресурсы получают ненулевые оценки, а недефицитные - нулевые.
2. Несимметричная пара взаимно двойственных задач.
Рассматривается каноническая задача линейного программирования (КЗЛП):

Двойственная задача имеет вид:

3. Общая постановка взаимодвойственных задач.
Рассматривается общая задача линейного программирования (ОЗЛП):
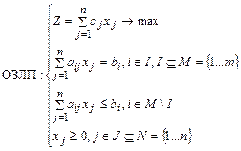
Двойственная задача:

Замечание: Неотрицательная переменная одной задачи соответствует ограничению-неравенству другой задачи, и наоборот, ограничение-неравенство одной задачи соответствует неотрицательной переменной другой задачи.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
1. Одна задача является задачей максимизации с ограничениями 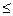 , другая является задачей минимизации с ограничениями
, другая является задачей минимизации с ограничениями  .
.
2. Каждому ограничению одной задачи соответствует переменная другой задачи. Номер переменной совпадает с номером ограничения.
3. Ограничению, записанному в виде неравенства, соответствует переменная двойственной задачи с условием неотрицательности.
4. Матрица условий одной задачи получается транспонированием матрицы условий другой задачи:
для исходной задачи  ,
,
для двойственной задачи 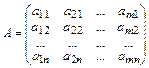 .
.
5. Коэффициенты целевой функции одной задачи соответствуют свободным членам системы ограничений другой задачи.
Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи:
1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду "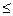 ", а если минимум — к виду "
", а если минимум — к виду " ",. Для этого неравенства, в которых данное требование не выполняется, умножить на (-1).
",. Для этого неравенства, в которых данное требование не выполняется, умножить на (-1).
2. Составить расширенную матрицу системы исходной задачи А, в которую включить матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.
3. Найти матрицу  , транспонированную к матрице А.
, транспонированную к матрице А.
4. Сформулировать двойственную задачу на основании полученной матрицы  и условия неотрицательности переменных.
и условия неотрицательности переменных.
Пример.1.Дана исходная задача линейного программирования:

Составить задачу, двойственную исходной задаче.
1. Так как исходная задача является задачей на максимизацию, то приведем все неравенства системы ограничений к виду "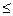 ", для этого обе части первого неравенства умножим на (-1).
", для этого обе части первого неравенства умножим на (-1).
Получим 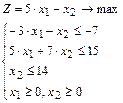 .
.
2. Составим расширенную матрицу системы А:  .
.
3. Найдем матрицу  , транспонированную к А:
, транспонированную к А: 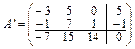 .
.
4. Сформулируем двойственную задачу:

Пример.2.Дана исходная задача линейного программирования:

Тогда двойственная задача будет иметь вид:
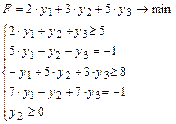 .
.
Основное неравенство теории двойственности.
Имеется пара взаимно двойственных задач. Для любых допустимых решений 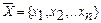 и
и  исходной и двойственной задач справедливо неравенство
исходной и двойственной задач справедливо неравенство 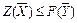 или
или 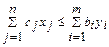 .
.
Достаточный признак оптимальности.
Если 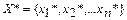 ,
,  - допустимые решения взаимно двойственных задач, для которых выполняется равенство
- допустимые решения взаимно двойственных задач, для которых выполняется равенство  , то
, то 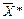 и
и  являются оптимальными решениями соответствующих задач.
являются оптимальными решениями соответствующих задач.
Первая теорема двойственности.
Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их функций равны:  .
.
Если целевая функция одной задачи не ограничена, то условия другой задачи несовместны.
Вторая теорема двойственности.
Предположим, дана симметричная пара взаимно двойственных задач.

Отсюда можно установить соответствие между первоначальными переменными одной из взаимно- двойственных задач и дополнительными переменными другой задачи:

 |

Для оптимальных значений переменных справедливы соотношения:
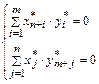
В силу условия неотрицательности переменных каждое из слагаемых должно равняться нулю:

Отсюда вытекает вторая теорема двойственности.
Положительным компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты решения другой задачи. То есть, если  ,то
,то 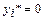 , а если
, а если  , то
, то  .
.
Третья теорема двойственности.
Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих свободных переменных целевой функции оптимального решения исходной задачи.
Компоненты оптимального решения двойственной задачи равны значениям частных производных целевой функции  по соответствующим аргументам т.е.
по соответствующим аргументам т.е.  и характеризуют на сколько вырастут доходы если соответствующий ресурс увеличить на одну единицу.
и характеризуют на сколько вырастут доходы если соответствующий ресурс увеличить на одну единицу.
Пример. Понятие двойственности рассмотрим на примере задачи оптимального использования ресурсов.
Для производства двух видов продукции  используется три вида сырья. Предприятие имеет сырья
используется три вида сырья. Предприятие имеет сырья  соответственно в количествах 50, 30, 60 единиц. От реализации единицы каждого вида продукции предприятие получит прибыль соответственно 17 руб. (
соответственно в количествах 50, 30, 60 единиц. От реализации единицы каждого вида продукции предприятие получит прибыль соответственно 17 руб. ( ), 25 руб. (
), 25 руб. ( ). Нормы расхода сырья на производство товаров вместе с данными о прибыли и запасах сырья представлены в следующей таблице:
). Нормы расхода сырья на производство товаров вместе с данными о прибыли и запасах сырья представлены в следующей таблице:
| Вид сырья | Нормы расхода сырья для производства единицы товара | Запасы | |

| 
| ||

| |||

| |||

| |||
| Прибыль |
Пусть 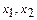 - объем производства товаров
- объем производства товаров 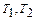 , обеспечивающий максимум прибыли.
, обеспечивающий максимум прибыли.
Математическая модель исходной (прямой) задачи:

Поставив в соответствие каждому ограничению-неравенству одной задачи неотрицательную переменную другой задачи, запишем математическую модель двойственной задачи:
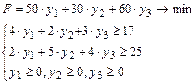
Решение взаимно двойственных задач представлено на следующих листа Mathcad:
Прямая задача (задача нахождения оптимального плана производства):

Таким образом, в результате решения прямой задачи получили оптимальный план производства:  Х, при котором следует производить оба вида продукции, и прибыль от реализации будет максимальной
Х, при котором следует производить оба вида продукции, и прибыль от реализации будет максимальной  рублей.
рублей.
Двойственная задача (задача нахождения оптимального набора оценок на ресурсы):

Решая двойственную задачу, нашли оптимальный набор оценок на ресурсы  , т.е. ресурсы
, т.е. ресурсы  и
и  по оптимальному плану полностью использованы, и объективно обусловленные оценки этих ресурсов ненулевые (данные ресурсы являются дефицитными). Ресурс
по оптимальному плану полностью использованы, и объективно обусловленные оценки этих ресурсов ненулевые (данные ресурсы являются дефицитными). Ресурс  не полностью используется, и объективно условленная оценка этого ресурса нулевая (ресурс недефицитный).
не полностью используется, и объективно условленная оценка этого ресурса нулевая (ресурс недефицитный).
7. Двойственный симплекс-метод
Двойственный симплекс-метод является методом, при котором сначала симплексным методом решается исходная задача, а затем оптимальное решение двойственной задачи находится с помощью теорем двойственности.
Пример. Составить и решить задачу, двойственную следующей задаче:

Решение.
Сформулируем задачу, двойственную для исходной задачи.
Поскольку исходная задача является задачей на отыскание максимума целевой функции, то для составления двойственной задачи, первоначально необходимо все ограничения-неравенства исходной задачи привести к виду, когда они имеют знак «≤». Для этого обе части неравенств со знаком «≥» умножим на (-1).
Тогда двойственная задача (задача минимизации целевой функции при ограничениях-неравенствах со знаком «≥») будет иметь вид:
 |



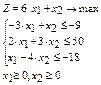
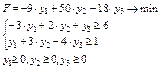
Используя теоремы двойственности, можно не решая двойственную задачу симплексным методом, на основе последней симплекс-таблицы оптимального решения исходной задачи получить последнюю симплекс-таблицу оптимального решения двойственной задачи.
В результате решения исходной задачи линейного программирования симплексным методом следующую симплекс-таблицу соответствующую оптимальному решению (см. Таб.3.).
Согласно первой теореме двойственности, если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их функций равны: 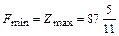 .
.
Установим соответствие между переменными исходной и двойственной задач (базисным переменным одной задачи соответствуют свободные переменные другой, и наоборот):

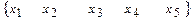

Положительным компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.

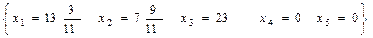

 Подставив найденные значения
Подставив найденные значения  в целевую функцию F, получим
в целевую функцию F, получим  , что и подтверждается первой теоремой двойственности.
, что и подтверждается первой теоремой двойственности.
Составим последнюю симплекс-таблицу оптимального решения двойственной задачи по следующим правилам:
ü Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции задачи, выраженной через свободные переменные её оптимального решения;
ü Матрица коэффициентов свободных переменных симплекс-таблицы оптимального решения двойственной задачи (кроме строки целевой функции) получается путем транспонирования матрицы коэффициентов свободных переменных симплекс-таблицы оптимального решения исходной задачи с противоположными знаками;
ü Коэффициенты при свободных переменных в строке целевой функции в симплекс-таблице оптимального решения двойственной задачи равны соответствующим свободным членам симплекс-таблицы оптимального решения исходной задачи (с противоположным знаком, если исходная задача является задачей максимизации).
В результате последняя симплекс-таблица оптимального решения двойственной задачи будет иметь вид:
| Базисные переменные | Свободные члены | Свободные переменные | ||
| y4 | y1 | y5 | ||
| y2 | 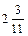
| 
| -1 | 
|
| y3 | 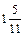
| 
| -1 | 
|
| F | 
| 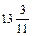
| -23 | 
|
 при
при  .
.
8. Задача целочисленного линейного программирования
Задача линейного программирования, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного линейного программирования.
Математическая модель:

 - целые.
- целые.
Для решения задач целочисленного линейного программирования используется ряд методов.
Методы отсечения.
Сущность методов отсечения состоит в том, что сначала задача решается без учета целочисленности. Если полученный оптимальный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
- Ограничение должно быть линейным;
- Ограничение должно исключать из ОДР найденный оптимальный нецелочисленный план;
- Ограничение не должно исключать из ОДР ни одно целочисленное решение.
Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Далее задача решается с учетом нового ограничения.
Метод Гомори (отсечения).
Этапы:
1. Решить симплекс-методом задачу линейного программирования без учета целочисленности. Если оптимальное решение целое, то это решение исходной задачи. Если целевая функция не ограничена, или ограничения несовместны, то решение целочисленной задачи линейного программирования не существует.
2. Если среди компонент есть нецелые, то необходимо выбрать компоненту с дробной частью и сформировать правильное отсечение- неравенство.
Предположим, что  - базисные переменные,
- базисные переменные,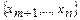 - свободные переменные.
- свободные переменные.
Оптимальное решение (из последней симплекс-таблицы) имеет вид 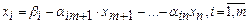 . В результате оптимальное решение запишется в виде
. В результате оптимальное решение запишется в виде 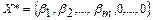 - нецелочисленное решение (
- нецелочисленное решение (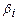 - нецелые).
- нецелые).
Составляется неравенство правильного отсечения:
 , где
, где  - дробная часть числа[1].
- дробная часть числа[1].
Правильное отсечение–неравенство преобразовать в уравнение путем введения неотрицательной целочисленной переменной и ввести это уравнение в систему ограничений.
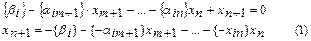
Соотношение (1) добавляется в последнюю симплекс-таблицу как дополнительная строка. В результате симплекс-таблица представляет недопустимое решение.
4.Полученная расширенная задача снова решается симплекс–методом. Если вновь полученное оптимальное решение нецелочисленное, то итерации повторяются.
Признак несуществования оптимального целочисленного решения: Если в процессе решения появляется уравнение (выражающее базисную переменную через свободные) с нецелым свободным членом и целыми коэффициентами при свободных переменных, то исходная задача не имеет целочисленного оптимального решения.
Пример. Найти решение задачи целочисленного линейного программирования:

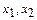 - целые
- целые
В результате решения данной задачи симплексным методом без условия целочисленности получили симплекс-таблицу, соответствующую оптимальному решению (см. Таб.3.) и оптимальное решение  при
при  .
.
Поскольку среди компонент оптимального решения есть нецелые (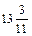 и
и 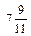 ), то для нахождения целочисленного оптимального решения среди нецелых компонент выбирается компонента с наибольшей дробной частью, и по соответствующей строке в симплекс-таблице формируется правильное отсечение.
), то для нахождения целочисленного оптимального решения среди нецелых компонент выбирается компонента с наибольшей дробной частью, и по соответствующей строке в симплекс-таблице формируется правильное отсечение.
Наибольшую дробную часть имеет  , т.к.
, т.к.
 .
.
Поэтому сформируем правильное отсечение - неравенство по строке, соответствующей этой компоненте.

Это неравенство введением дополнительной неотрицательной целочисленной переменной преобразуем в равносильное уравнение:

Полученное соотношение добавляем в симплекс-таблицу дополнительной строкой (свободный член вносим без изменения знака, а коэффициенты при свободных переменных - с противоположным знаком).
| Базисные переменные | Свободные члены | Свободные переменные | |
| x4 | x5 | ||
| x1 | 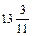
| 
| 
|
| x3 | |||
| x2 | 
| 
| 
|
| x6 | 
|  
| 
|
| Z | 
| 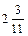
| 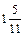
|
Полученную расширенную задачу решаем симплекс-методом.
Базисное решение  - недопустимое, т.к. имеется отрицательный элемент, ограничения совместны (в строке, имеющей отрицательный свободный член есть отрицательные элементы).
- недопустимое, т.к. имеется отрицательный элемент, ограничения совместны (в строке, имеющей отрицательный свободный член есть отрицательные элементы).
Столбец, соответствующий  , принимаем в качестве разрешающего. Для определения разрешающей строки найдем минимальное положительное отношение свободных членов к элементам разрешающего столбца:
, принимаем в качестве разрешающего. Для определения разрешающей строки найдем минимальное положительное отношение свободных членов к элементам разрешающего столбца:  .
.
Базисную переменную  переводим в свободные переменные, а свободную переменную
переводим в свободные переменные, а свободную переменную  - в базисные.
- в базисные.
В результате преобразования симплекс-таблицы получим:
| Базисные переменные | Свободные члены | Свободные переменные | |
| x6 | x5 | ||
| x1 | -3 | ||
| x3 | -8 | ||
| x2 | -1 | ||
| x4 | -11 |  9 9
| |
| Z | -19 |
Базисное решение  - допустимое, т.к. в столбце свободных членов нет ни одного отрицательного элемента, но неоптимальное (в строке целевой функции, кроме столбца свободных членов, элементы не одного знака). Целевая функция ограничена сверху, т.к. в столбце, не удовлетворяющем признаку оптимальности, есть положительные элементы.
- допустимое, т.к. в столбце свободных членов нет ни одного отрицательного элемента, но неоптимальное (в строке целевой функции, кроме столбца свободных членов, элементы не одного знака). Целевая функция ограничена сверху, т.к. в столбце, не удовлетворяющем признаку оптимальности, есть положительные элементы.
Столбец, не удовлетворяющий признаку оптимальности ( ), принимаем в качестве разрешающего. Разрешающей является строка
), принимаем в качестве разрешающего. Разрешающей является строка  , т.к.
, т.к. 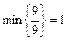 .
.
Базисную переменную  переводим в свободные переменные, а свободную переменную
переводим в свободные переменные, а свободную переменную  - в базисные.
- в базисные.
Преобразуем симплекс-таблицу:
| Базисные переменные | Свободные члены | Свободные переменные | |
| x6 | x4 | ||
| x1 | 
| 
| |
| x3 | 
| 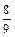
| |
| x2 | 
| 
| |
| x5 | 
| 
| |
| Z | 
| 
|
Базисное решение  - допустимое, т.к. в столбце свободных членов нет ни одного отрицательного элемента, и оптимальное (в строке целевой функции все элементы положительные (одного знака)).
- допустимое, т.к. в столбце свободных членов нет ни одного отрицательного элемента, и оптимальное (в строке целевой функции все элементы положительные (одного знака)).
Найденное оптимальное решение целочисленное, следовательно, задача целочисленного программирования решена.
Максимальное значение целевой функции  при
при  .
.
9. Транспортная задача
Постановка транспортной задачи.
У m поставщиков  сосредоточен однородный груз в количествах соответственно
сосредоточен однородный груз в количествах соответственно  . Имеющийся груз необходимо доставить n потребителям
. Имеющийся груз необходимо доставить n потребителям  , спрос которых равен соответственно
, спрос которых равен соответственно  . Известна стоимость перевозки единицы груза от i – го поставщика к j - му потребителю -
. Известна стоимость перевозки единицы груза от i – го поставщика к j - му потребителю -  . Требуется найти оптимальный план перевозок, обеспечивающий минимальные затраты и вывоз грузов и удовлетворение потребностей.
. Требуется найти оптимальный план перевозок, обеспечивающий минимальные затраты и вывоз грузов и удовлетворение потребностей.
Экономико-математическая модель задачи.
Пусть  - количество единиц груза, которое необходимо доставить от i – го поставщика к j - му потребителю.
- количество единиц груза, которое необходимо доставить от i – го поставщика к j - му потребителю.
Целевая функция:
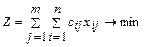 (1)- минимизация общих затрат на реализацию плана перевозок.
(1)- минимизация общих затрат на реализацию плана перевозок.
Ограничения на запасы поставщиков:
 (2) - все запасы должны быть вывезены.
(2) - все запасы должны быть вывезены.
Ограничения на спрос потребителей:
 (3) - все потребности должны быть удовлетворены.
(3) - все потребности должны быть удовлетворены.
Условия неотрицательности:
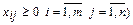 (4)
(4)
Модель транспортной задачи называют закрытой, если суммарный объём груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т.е. выполняется условие  . Если это условие не выполняется (
. Если это условие не выполняется ( ), то модель транспортной задач называется открытой.
), то модель транспортной задач называется открытой.
Если  , то открытая транспортная задача сводится к закрытой путем ведения фиктивного потребителя с объемом потребностей
, то открытая транспортная задача сводится к закрытой путем ведения фиктивного потребителя с объемом потребностей  и стоимостями перевозок, равными нулю. Если
и стоимостями перевозок, равными нулю. Если 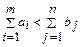 , то вводится фиктивный поставщик с объемом груза
, то вводится фиктивный поставщик с объемом груза  и стоимостями перевозок, равными нулю.
и стоимостями перевозок, равными нулю.
Число переменных  в транспортной задаче с m поставщиками и n потребителями равно nm, а число уравнений в системах (2) и (3) равно n+m. Так как предполагается, что выполняется условие
в транспортной задаче с m поставщиками и n потребителями равно nm, а число уравнений в системах (2) и (3) равно n+m. Так как предполагается, что выполняется условие  , то число линейных независимых уравнений равно n+m-1. Следовательно, опорный план транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.
, то число линейных независимых уравнений равно n+m-1. Следовательно, опорный план транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно n+m-1, то план является невырожденным, а если меньше – то вырожденным.
Транспортная задача является канонической задачей линейного программирования, и для ее решения в принципе можно использовать симплекс-метод. Однако, в силу специфичности транспортной задачи, используются более эффективные методы.
Алгоритм решения транспортной задачи (методом потенциалов).
1. Определяется исходный план (метод северо-западного угла, метод минимальной стоимости и др.).
2. Производится оценка плана.
3. Осуществляется переход к следующему плану.
Получение исходного плана основано на заполнении следующей таблицы:

| …… | 
| …… | 
| ||
| 

| …… | 

| …… | 

|

|
| …… | …… | …… | ……. | …… | …… | |

| 
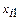
| …… | 

| …… | 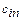

|

|
| …… | …… | …… | ……… | …… | …… | |

| 
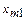
| …… | 

| …… | 
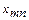
|

|

| 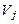
| 
|
В каждой ячейке в левом верхнем углу помещаются стоимости перевозок, в правом нижнем углу объемы поставок от i -го поставщика к j- му потребителю. В верхней строке указываются мощности поставщиков, в левом столбце – спрос потребителей.
Рассмотрим методы получения первого опорного плана.
а) Метод северо-западного угла.
Рассматривается незаполненная левая верхняя ячейка. Эта ячейка заполняется минимальным значением от возможного объема поставок и объема потребностей. В результате или будут удовлетворены все потребности, или исчерпаны запасы поставщика. Если удовлетворены потребности, то остальные ячейки этого столбца зачеркиваются и в последующих распределениях не участвуют.
Если исчерпаны запасы поставщика, то зачеркиваются остальные ячейки соответствующей строки, и они не участвуют в последующих распределениях.
Вновь рассматривается незаполненная северо-западная ячейка, и итерации повторяются.
Замечание. Этот метод не учитывает стоимость перевозок, и поэтому исходный план может оказаться далеким от оптимального.
б) Метод минимальной стоимости.
Из всех незаполненных ячеек находится ячейка с минимальной стоимостью перевозок. Эта ячейка заполняется минимальным значением от возможного объема поставок и объема потребностей. В результате или будут удовлетворены потребности, или исчерпаны запасы.
Если исчерпаны запасы, зачеркиваются остальные ячейки соответствующей строки, и они не участвуют в последующих распределениях.
Если удовлетворены все потребности, то зачеркиваются остальные ячейки соответствующего столбца, и они не участвуют в последующих распределениях.
Вновь из всех незаполненных ячеек находится ячейка с минимальной стоимостью, итерации повторяются.
Если план получается вырожденным, т.е. m+n-1 не совпадает с числом заполненных ячеек, то вводится фиктивно заполненная нулем ячейка. Для этого из всех незаполненных ячеек находится ячейка с минимальной стоимостью. Если на основе этой ячейки невозможно построить замкнутый цикл со всеми заполненными вершинами, то она принимается в качестве фиктивной. В обратном случае эта ячейка исключается из рассмотрения претендентов на фиктивную ячейку.
Для оценки плана:
1) Вычисляются потенциалы поставщиков 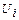 и потребителей
и потребителей  . Потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию
. Потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию  (5).
(5).
Для получения решения системы уравнений (5) используется тождество  .
.
2) Вычисляются оценки свободных ячеек 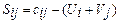
Если все  , то план оптимальный. Если для всех ячеек
, то план оптимальный. Если для всех ячеек  , то оптимальный план является единственным. Если какая-либо оценка
, то оптимальный план является единственным. Если какая-либо оценка  , то существует бесчисленное множество решений с одинаковым значением целевой функции (решение оптимальное, но альтернативное). Если какое-либо значение
, то существует бесчисленное множество решений с одинаковым значением целевой функции (решение оптимальное, но альтернативное). Если какое-либо значение  , то план неоптимальный, и необходимо произвести загрузку свободной ячейки (получение новой таблицы).
, то план неоптимальный, и необходимо произвести загрузку свободной ячейки (получение новой таблицы).
Для перехода к следующему опорному плану для ячейки с минимальной отрицательной оценкой строится замкнутый цикл с вершинами в заполненных ячейках (Замкнутый цикл – это ломаная линия (возможно, прямоугольник), вершинами которой являются заполненные ячейки, кроме одной свободной ячейки с минимальной отрицательной оценкой).
В свободную вершину цикла вписывается “+”, а все последующие вершины по часовой стрелке будут иметь “-”, “+”, “-”,…
Находится минимальный объем груза для всех отрицательных вершин цикла. В вершинах цикла со знаком «+» объем увеличивается на эту величину, в вершинах со знаком «-» - уменьшается. В результате баланс распределения не нарушается.
Затем снова производится оценка опорного плана.
Замечание: Если полученный опорный план вырожденный, то необходимо выбрать свободную ячейку с минимальной стоимостью без образования замкнутого цикла с заполненными вершинами и в эту ячейку вписать ноль.
Рассмотрим пример решения транспортной задачи.
Пример. Предприятие имеет 3 склада готовой продукции: А1, А2, А3, на которых соответственно имеются 70, 90 и 60 единиц товара. Рынкам сбыта, находящимся в городах B1, B2, B3, B4, необходимо распределить следующее количество единиц продукции – 90, 40, 50 и 20. Стоимость перевозки единицы продукции со склада на рынок сбыта задается таблицей (в у.е.):
| Склады | Мощность складов | Потребности рынков сбыта | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
Необходимо составить план распределения товаров между рынками сбыта, обеспечивающий минимальные транспортные издержки.
Составим экономико-математическую модель данной задачи.
Обозначим через  - объём перевозки от i –ого склада j – ому рынку сбыта.
- объём перевозки от i –ого склада j – ому рынку сбыта.
Тогда суммарные затраты на перевозку Z составят:

Заданные мощности складов и потребности рынков сбыта накладывают ограничения на значения объемов перевозок  :
:
- Мощности всех складов должны быть реализованы:
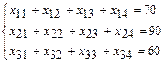
- Спросы потребителей должны быть удовлетворены:

- Объемы перевозимых грузов не могут быть отрицательными:
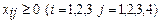
Решение.
1. Определим характер транспортной задачи.
Так как  (суммарные мощности не равны суммарным потребностям), то данная задача является открытой и необходимо её привести к закрытой. Для этого введем фиктивного потребителя (рынок сбыта), потребность которого составляет
(суммарные мощности не равны суммарным потребностям), то данная задача является открытой и необходимо её привести к закрытой. Для этого введем фиктивного потребителя (рынок сбыта), потребность которого составляет 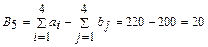 . Все значения стоимости перевозок для этого потребителя
. Все значения стоимости перевозок для этого потребителя  .
.
После введения фиктивного потребителя задача становится закрытой, и её можно решить методом потенциалов.
2. Заполним распределительную таблицу исходными данными.
В результате введения фиктивного потребителя распределительная таблица исходных данных примет вид:
3. Составим первый опорный план методом «минимальной стоимости».
В первую очередь заполняется ячейка с минимальной стоимостью. Это ячейки с нулевой стоимостью. Сравним максимально возможные поставки для этих ячеек: для ячейки (1,5) 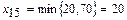 , для ячейки (2,5)
, для ячейки (2,5)  , для ячейки (3,5)
, для ячейки (3,5)  . Так как для ячеек (1,5), (2,5) и (3,5) эти значения равны, то произведем максимально возможную поставку в любую из них. Например, в ячейку (1,5) даем поставку, равную 20. В результате потребность фиктивного рынка сбыта удовлетворена, и последний столбец таблицы поставок выпадает из рассмотрения.
. Так как для ячеек (1,5), (2,5) и (3,5) эти значения равны, то произведем максимально возможную поставку в любую из них. Например, в ячейку (1,5) даем поставку, равную 20. В результате потребность фиктивного рынка сбыта удовлетворена, и последний столбец таблицы поставок выпадает из рассмотрения.
В оставшейся таблице наименьшей стоимостью, равной 1, обладает ячейка (1,2). Поскольку на складе в наличии имеется 70-20 = 50 единиц товара, то мы можем полностью удовлетворить потребность 2-ого рынка сбыта, и 2-ой столбец выпадает из дальнейшего рассмотрения.
| 1 40 | 0 20 | |||||
Далее заполняем ячейку (1,1), т.к. она обладает наименьшей стоимостью перевозки, равной 2. Потребность 2-ого склада равна 90 единицам товара, но с 1-ого склада ранее были вывезены 40 единиц товара для 2-ого рынка сбыта и 20 единиц товара для 5-ого склада. Поэтому на 1-ый рынок сбыта мы можем поставить только 10 единиц товара, и товары, находившиеся в наличии 1-ого склада, полностью вывезены, т.е. 1-ая строка выпадает из дальнейшего рассмотрения.
| 2 10 | 1 40 | 0 20 | ||||
В оставшейся таблице минимальными стоимостями (равной 3) обладают ячейки (2,3) и (3,1). Потребность 3-ого рынка сбыта равна 50 единицам товара, и 2-ой склад (его мощность составляет 90 единиц товара) может полностью её удовлетворить. Потребность 1-ого рынка сбыта равна 60 единицам товара, и 1-ый склад также может полностью её удовлетворить (оставшаяся мощность равна 90 - 10=80 единиц).
Максимально возможную поставку, равную 60 единицам, произведем в ячейку (1,3), тогда последняя строка выпадает из рассмотрения.
| 2 10 | 1 40 | 0 20 | ||||
| 3 60 | ||||||
Рассуждая аналогичным образом, заполним оставшуюся часть распределительной таблицы. В результате получим:
| 2 10 | 1 40 | 0 20 | ||||
| 5 20 | 3 50 | 5 20 | ||||
| 3 60 | ||||||
4. Проверим полученный опорный план на невырожденность.
Число заполненных ячеек распределительной таблицы равно 7. Для выполнения условия невырожденности плана необходимо, чтобы число заполненных ячеек равнялось 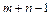 , где m – число поставщиков (складов), n – число потребителей (рынков сбыта).
, где m – число поставщиков (складов), n – число потребителей (рынков сбыта).
Для данной задачи значение  совпадает с число заполненных ячеек. Таким образом, построенный опорный план является невырожденным.
совпадает с число заполненных ячеек. Таким образом, построенный опорный план является невырожденным.
5. Определим потенциалы поставщиков 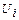 и потребителей
и потребителей  .
.
Потенциалы поставщиков и потребителей определяются для заполненных ячеек распределительной таблицы из уравнений  . При этом предполагается, что
. При этом предполагается, что  . Потенциалы складов размещаются в крайнем правом углу, потенциалы рынков сбыта - в нижней строке распределительной таблицы.
. Потенциалы складов размещаются в крайнем правом углу, потенциалы рынков сбыта - в нижней строке распределительной таблицы.
| 2 10 | 1 40 | 0 20 | U1 | |||
| 5 20 | 3 50 | 5 20 | U2 | |||
| 3 60 | U3 | |||||
| V1 | V2 | V3 | V4 | V5 |
Для определения потенциалов составляем уравнения:

Положив  , получим
, получим 
| 2 10 | 1 40 | 0 20 | ||||
| 5 20 | 3 50 | 5 20 | ||||
| 3 60 | ||||||
6. Проверим опорный план на оптимальность.
Для проверки опорного плана на оптимальность, необходимо вычислить оценки всех свободных ячеек по формуле 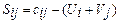 . Если полученные значения
. Если полученные значения  , то найденный план оптимальный. При этом если какая-либо оценка
, то найденный план оптимальный. При этом если какая-либо оценка  , то оптимальный план неединственный, т.е. существует бесконечное множество решений с одним и тем же значением целевой функции. В случае, если все оценки
, то оптимальный план неединственный, т.е. существует бесконечное множество решений с одним и тем же значением целевой функции. В случае, если все оценки 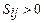 , то оптимальный план единственный.
, то оптимальный план единственный.
Если какая-либо из оценок 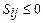 , то план неоптимальный и необходимо произвести перераспределение поставок (произвести загрузку свободной ячейки с отрицательной оценкой).
, то план неоптимальный и необходимо произвести перераспределение поставок (произвести загрузку свободной ячейки с отрицательной оценкой).
Вычислим оценки свободных ячеек:

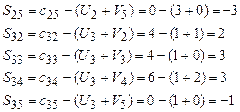
Среди полученных оценок есть отрицательные, значит, найденный опорный план неоптимальный, и следует произвести загрузку свободной ячейки с минимальной оценкой и перейти к новому опорному плану.
В качестве такой ячейки выберем ячейку (2,5), т.к. она имеет наименьшую оценку  .
.
7. Построим новый опорный план.
Для выбранной свободной ячейки с минимальной отрицательной оценкой необходимо построить замкнутый цикл с вершинами в заполненных ячейках. (Замкнутый цикл – это ломаная, вершинами которой являются заполненные ячейки, кроме одной свободной ячейки с отрицательной оценкой).
Построим следующий замкнутый цикл: (2,5) – (2,1) – (1,1) – (1,5) – (2,5). В свободную ячейку с минимальной отрицательной оценкой вписывается знак «+», в вершину, следующую за свободной клеткой в цикле, ставится знак «-» и т.д. по порядку.
|  2 10 2 10
| 1 40 |
20 | |||||||
| 5 20 | 3 50 | 5 20 |
| ||||||
| 3 60 | ||||||||||
Поставка, передаваемая по циклу, определяется как минимум среди поставок в ячейках цикла со знаком «-». Для нашей задачи знак «-» имеют ячейки (2,2), (1,5). Минимальный объем груза для этих ячеек равен 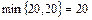 .
.
В вершинах цикла со знаком «+» объем груза увеличивается на 20 единиц, а в вершинах со знаком «-» - уменьшается на тот же объем груза. Например, поставка ячейки (2,5) станет равной 20 единицам груза, ячейки (2,1) и (1,5) станут свободными и т.д. Поскольку ячейки со знаком «-» имеют одинаковый объем поставок, равный 20, то для сохранения невырожденности плана ячейку (1,5) (данная ячейка является клеткой с минимальной стоимостью, и на её основе нельзя построить замкнутого цикла) будем считать условно заполненной с объемом поставки, равным 0.
В результате баланс распределения поставок не нарушается.
Проверим новый опорный план на оптимальность. Снова найдем оценки свободных ячеек. Для этого сначала вычислим потенциалы складов и рынков сбыта заполненных ячеек.
| 2 30 | 1 40 |
|
 3 3
| 0 0 | ||||||
50 |
20 | 0 20 | ||||||||
| 3 60 | ||||||||||
Положив  , получим
, получим 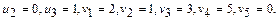
Вычислим оценки свободных ячеек:

Среди полученных оценок есть отрицательные, значит, найденный опорный план неоптимальный, и следует произвести загрузку свободной ячейки с минимальной оценкой и перейти к новому опорному плану. В качестве такой ячейки выберем ячейку (1,4), т.к. она имеет наименьшую оценку  .
.
Построим следующий замкнутый цикл: (1,4) – (1,5) – (2,5) – (2,4) – (1,4). Определяем поставку, передаваемую по циклу, как  . В вершины цикла со знаком «+» объем груза условно увеличивается на 0 единиц груза, а в вершинах со знаком «-» - уменьшается на тот же объем.
. В вершины цикла со знаком «+» объем груза условно увеличивается на 0 единиц груза, а в вершинах со знаком «-» - уменьшается на тот же объем.
Ячейка (1,5) становится свободной, ячейка (1,4) – становится условной заполненной. Поставки в остальных ячейках цикла остаются неизменными.
| 2 30 | 1 40 | 3 0 | ||||
| 3 50 | 5 20 | 0 20 | ||||
| 3 60 | ||||||
| -2 |
Проверим новый опорный план на оптимальность. Снова найдем оценки свободных ячеек. Для этого сначала вычислим потенциалы складов и рынков сбыта заполненных ячеек.
Положив  , получим
, получим 
Вычислим оценки свободных ячеек:
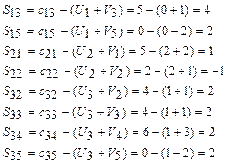
Полученный опорный план снова неоптимальный, т.к. среди оценок свободных ячеек есть отрицательные (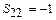 ).
).
Произведем перераспределение поставок, осуществив загрузку ячейки с отрицательной оценкой.
Построим замкнутый цикл: (2,2) – (1,2) – (1,4) – (2,4) – (2,2).
30 |  1 40 1 40
| 
| ||||||||
|
50 | 5 20 | 0 20 | |||||||
| 3 60 | ||||||||||
| -2 |
Произведем загрузку свободной ячейки с отрицательной оценкой.
Поставка, передаваемая по циклу, определяется как минимум среди поставок в ячейках цикла со знаком «-». Для нашей задачи знак «-» имеют ячейки (1,2), (2,4). Минимальный объем груза для этих ячеек равен 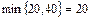 .
.
Поставка ячейки (2,2) станет равной 20 единицам груза, ячейки (1,2) - 20 единицам груза, ячейки (1,4) - 20 единицам груза, ячейка (2,4) станет свободной.
В результате получим новый опорный план, который необходимо проверить на оптимальность.
| 2 30 | ||||||||

| ||||||||
| -1 |
Вычислим потенциалы поставщиков и потребителей для заполненных ячеек.
Положив  , получим
, получим 
Вычислим оценки свободных ячеек:

Все полученные оценки неотрицательные  , значит, найденный опорный план оптимальный. Поскольку среди оценок
, значит, найденный опорный план оптимальный. Поскольку среди оценок 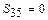 , то оптимальный план неединственный, и можно, произведя загрузку ячейки (3,5), найти бесконечное множество решений, при которых целевая функция будет иметь одно и то же значение.
, то оптимальный план неединственный, и можно, произведя загрузку ячейки (3,5), найти бесконечное множество решений, при которых целевая функция будет иметь одно и то же значение.
Оптимальный план распределения:
 , для которого значение целевой функции (минимальные транспортные издержки)
, для которого значение целевой функции (минимальные транспортные издержки)  у.е.
у.е.
Двадцать единиц продукции, находящиеся на 2-ом складе, согласно полученному плану остаются нераспределенными.
10. Задачи производственного менеджмента
1. Задача распределения ресурсов с ограничениями на технико-экономические показатели
Задача распределения ресурсов с ограничениями на технико-экономическиеможет быть сформулирована следующим образом.
Имеется целевая функция
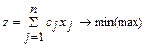
при ограничениях:

при граничных условиях:
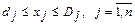 .
.
Моделируемая система характеризуется производством нескольких видов продукции ( ), для выпуска которых требуются имеющиеся в ограниченном количестве различные ресурсы
), для выпуска которых требуются имеющиеся в ограниченном количестве различные ресурсы 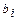 (
(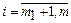 ). Расход i – ого ресурса на единицу продукции j – ого вида равен
). Расход i – ого ресурса на единицу продукции j – ого вида равен 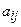 .
.
Заданы также общие для системы показатели 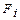 (
(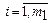 ), определяющие её деятельность и выполнение которых является обязательным (как правило, это планируемые технико-экономические показатели). Коэффициенты
), определяющие её деятельность и выполнение которых является обязательным (как правило, это планируемые технико-экономические показатели). Коэффициенты  обозначают единичную эффективность j – ого вида продукции по i –ому показателю (
обозначают единичную эффективность j – ого вида продукции по i –ому показателю (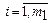 ).
).
При заданном потреблении ресурсов показатель эффективности j – ого вида продукции характеризуется величиной  .
.
Необходимо найти такой план производства каждого вида продукции, при котором оптимизируется общая эффективность производства при удовлетворении ограничений на обобщенные показатели, на используемые ресурсы и граничных условий на значения переменных  (ограничения по объёмам минимального
(ограничения по объёмам минимального  (обязательства предприятия) и максимального
(обязательства предприятия) и максимального  (ёмкость рынка) выпусков продукции каждого вида).
(ёмкость рынка) выпусков продукции каждого вида).
2. Задача размещения производства
Предположим, есть план производства n видов продукции -  (Значения
(Значения  получают в результате решения задачи оптимального планирования производства). Для производства используются k видов взаимозаменяемого оборудования (технологических линий или станков).
получают в результате решения задачи оптимального планирования производства). Для производства используются k видов взаимозаменяемого оборудования (технологических линий или станков).
Оборудование каждого вида с учетом текущего и капитального ремонта не может использоваться более  количества времени за планируемый период. Известна производительность k - ого оборудования:
количества времени за планируемый период. Известна производительность k - ого оборудования: 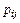 - количество продукции j -го вида, производимое i -ым видом оборудования за единицу времени. Предположим, затраты i -го оборудования для производства j -ой продукции в единицу времени составляет
- количество продукции j -го вида, производимое i -ым видом оборудования за единицу времени. Предположим, затраты i -го оборудования для производства j -ой продукции в единицу времени составляет 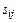 . Определить оптимальную загрузку оборудования
. Определить оптимальную загрузку оборудования 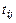 (количество времени, затраченного оборудованием каждого вида для производства каждого вида продукции).
(количество времени, затраченного оборудованием каждого вида для производства каждого вида продукции).
Экономико-математическая модель задачи:
Целевая функция (затрат) 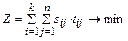
Ограничения:  (Оборудование каждого вида не может быть загружено более, чем на время Ti);
(Оборудование каждого вида не может быть загружено более, чем на время Ti);
 (Суммарный объем производства j – ой продукции на оборудовании всех видов составляет
(Суммарный объем производства j – ой продукции на оборудовании всех видов составляет  );
);
 .
.
3. Задача «коммивояжера»
Требуется объехать n пунктов, начиная и заканчивая в одном пункте, таким образом, чтобы суммарные затраты были минимальные. Затраты, связанные с переездом из i – ого пункта в j – ый пункт равны  .
.
 Математическая формулировка такой задачи сводится к виду:
Математическая формулировка такой задачи сводится к виду:
Целевая функция
 - минимизация суммарного времени.
- минимизация суммарного времени.
Ограничения – условия о выезде из каждого i – ого пункта только один раз и въезде в каждый j – ый пункт только один раз (i, j – соответственно номера пунктов выезда и приезда):
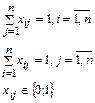
Задание для самостоятельной работы
Содержание:
1. Ознакомиться с теоретическим материалом.
2. Выполнить следующие задания.
2.1. Привести пример производственно-экономической задачи, сводящейся к задаче линейного программирования, и её математическую формулировку. Полученную задачу решить в Mathcad.
2.2. Математически сформулировать двойственную задачу, решить её в Mathcad и привести экономическую интерпретацию взаимодвойственных задач.
2.3. Найти наибольшее и наименьшее значения целевой функции Z при заданных ограничениях графическим методом.
2.4. Найти наибольшее значение целевой функции при заданных ограничениях симплекс-методом.
2.5. Сформулировать задачу, двойственную задаче 2.4., и решить её на основе теорем двойственности.
2.6. Найти целочисленное решение задачи линейного программирования 2.4.
2.7. Решить транспортную задачу с закрытой и открытой моделью.
Варианты задач для самостоятельной работы
1). Решить стандартную задачу линейного программирования:
1. 
2. 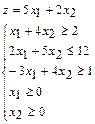
3. 
4. 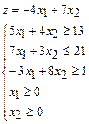
5. 
6. 
7. 
8. 
9. 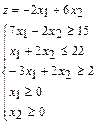
10. 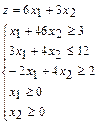
11. 
12. 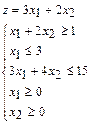
13. 
14. 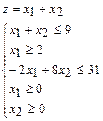
15. 
16. 
17. 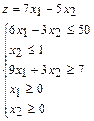
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 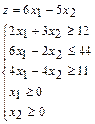
28. 
29. 
30. 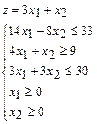
31. 
32. 
33. 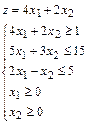
2). Решить транспортную задачу.
1. С трех складов  необходимо доставить овощи в пять торговых точек
необходимо доставить овощи в пять торговых точек 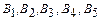 . Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной.
. Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной.
Числовые данные задачи представлены в следующей таблице:
| Склады | Торговые точки | Объём вывоза, т | ||||

| 
| 
| 
| 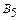
| ||
| Стоимость перевозки 1 т груза, руб | ||||||



| a d | e | b c | f | ||
| Объём вывоза, т |
Варианты задач:
| Вариант | a | b | c | d | e | f | Вариант | a | b | c | d | e | f |
2. На четыре строительные площадки 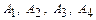 поступает кирпич с трех заводов
поступает кирпич с трех заводов  . Суточная потребность в кирпиче на строительных площадках равна соответственно: 40, 25, 35 и 40 тыс. шт. Производительность заводов за день составляет соответственно 30, 50, 45 тыс. шт.
. Суточная потребность в кирпиче на строительных площадках равна соответственно: 40, 25, 35 и 40 тыс. шт. Производительность заводов за день составляет соответственно 30, 50, 45 тыс. шт.
Транспортные расходы заводов на перевозку на 1 тыс. шт. по строительным площадкам (в тыс. руб.) приведены в следующей таблице:
| Заводы | Строительные площадки | Производи-тельность заводов за день, тыс. шт. | |||

| 
| 
|
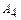
| ||
| Транспортные расходы на 1 тыс. шт., тыс. руб. | |||||



| b | с d | a e | ||
| Суточная потребность, тыс. шт. |
Варианты задач:
| Вариант | a | b | c | d | e | f | Вариант | a | b | c | d | e | f |
Литература
1. Кузнецов А.В. и др. Высшая математика: Мат. программир.: учеб./А.В. Кузнецов, В.А. Сакович, Н.И. Холод; Под общ. ред. А.В. Кузнецова. – Мн.: Высш. шк., 1994. – 286 с.: ил.
2. Справочник по оптимизационным задачам в АСУ/В.А. Бункин, Д.Колев, Б.Я. Курицкий, А.Н. Максименко, Ю.А. Сокуренко, А. Стоев. – Л.: Машиностроение, 1984. – 212 с., ил.
3. Исследование операций в экономике: учебн. пособие для вузов/ Н.Ш.Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2000. – 407 с.
4. Линейное программирование: методическое руководство для самостоятельной работы студентов. – Набережные Челны: КамПИ, 1989. – 27 с.
5. Плис А.И., Сливина Н.А. Mathcad 2000 Математический практикум для экономистов и инженеров: учеб. пособие. – М.: Финансы и статистика, 2000. – 656 с.: ил.
6. Экономико-математические модели и методы. Линейное программирование: учебное пособие для студентов экономических специальностей/Составители: Смирнов Ю.Н., Шибанова Е.В., Набережные Челны: Изд-во КамПИ, 2004, 81 с.
[1] Целой частью числа а называется наибольшее целое число [а], не превосходящее само число а. Дробной частью числа а называется число {а}, равное разности между этим числом и его целой частью {а} = а - [а]. Пример: 1.,,; 2.,,.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1048; Нарушение авторских прав?; Мы поможем в написании вашей работы!