Головні радіуси кривизни в даній точці еліпсоїда

Тоді

Або

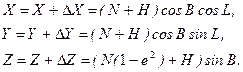(2.34)

Обернені залежності будуть мати наступний вид

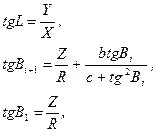
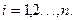(2.35)

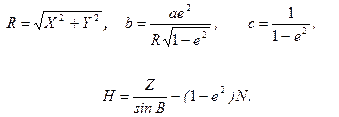
Вираз для обчислення довготи 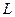знаходимо аналогічно (2.33), а обчислення широти 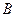, як видно із (2.35) вимагає застосування процесу наближень. Формула для 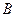отримана наступним чином. На основі рівнянь (2.34), після нескладних перетворень, можемо отримати

,

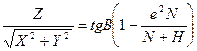а також

.

,

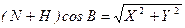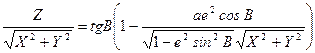або

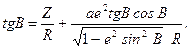(2.36)

Поділимо чисельник і знаменник у другому доданку (2.36) на 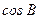і в результаті перетворень отримаємо

,

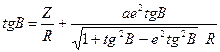а домноживши знаменник другого доданку ще на 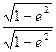та після деяких перетворень, остаточно отримаємо формулу, яка після відповідних позначень буде відповідати (2.35).

Що стосується переходу від поверхневих еліпсоїдних координат B,L до плоских x,y, то вид формул залежить від способу зображення (проекції) поверхні еліпсоїда на площині. Для проекції Гаусса-Крюгера формули зв'язку приведенні при розгляді відповідної теми у розділі 4.

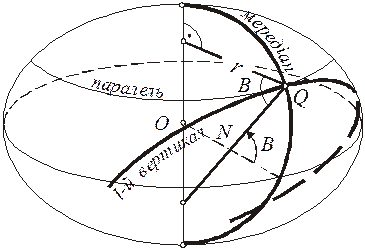
В будь-якій точці поверхні еліпсоїда обертання головними нормальними перерізами є:

1) меридіальний переріз, тобто нормальний переріз, що проходять через задану точку 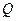і полюси еліпсоїда ;

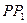2) переріз першого вертикалу, що проходить через точку 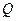і перпендикулярний до меридіального перерізу точки .

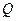Радіус кривини меридіального перерізу буде радіусом кривини плоскої кривої, від обертання якої утворилась дана поверхня обертання. У сфероїдній геодезії він позначається буквою М. Радіус кривини другого головного перерізу - N. Вказані радіуси аналогічні радіусам 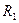та 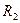(див. розділ 1, п.1.6).

Згідно теореми Меньє (1.6), радіус кривини першого вертикалу 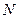буде рівний радіусу паралелі r, поділеному на косинус кута між площиною паралелі та нормаллю до поверхні

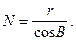(2.37)

Це означає, що радіус кривини головного перерізу, перпендикулярного до меридіального, рівний відрізку нормалі до поверхні від поверхні до осі обертання (рис 2.5).

Радіуси кривини M та N, як функції широти В даної точки, застосовуються в багатьох теоретичних і практичних розрахунках. У функції широти радіус кривини меридіана М може бути виражений через формули (1.2) або через коефіцієнти першої та другої квадратичних форм поверхні (1.7).

На основі другої групи формул (1.2) та з врахуванням рівняння (2.10) в редакції (2.13) для радіуса кривини меридіана запишемо

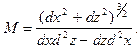
Рис. 2.5

Підставивши у вищенаведену формулу значення похідних, отримаємо вираз для радіуса кривини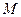

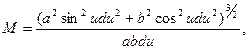
або

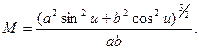(2.38)

Вираз (2.38) можна перетворити

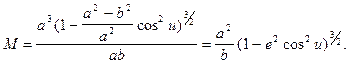
З врахуванням першої формули (2.20) та формули (2.21), остаточний вираз для радіуса кривини меридіана 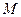буде мати вид

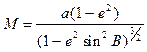. (2.39)

З врахуванням (2.11) вираз для радіуса кривини першого вертикалу буде

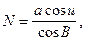
а використовуючи першу із формул (2.20), остаточно отримаємо

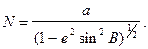(2.40)

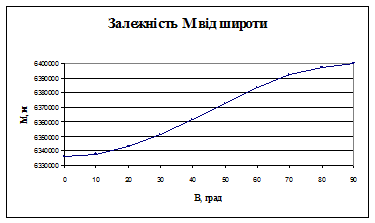
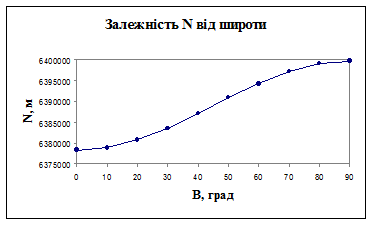
Величини М та N характеризують форму поверхні еліпсоїда в околицях даної точки і в подальшому постійно будуть нами використовуватися. Графічно, залежність радіусів кривини 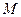і 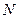від широти 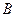, показана на рис. 2.6 а) і б) відповідно.

а)

б)

Рис. 2.6

Більшим за значенням є радіус кривини 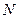. Дійсно, згідно формул (2.39) і (2.40), маємо

.

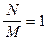тільки при В=90°, тобто на полюсі, де радіус кривини

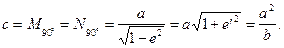(2.41)

Відношення різниці головних радіусів кривини до меншого із них може бути виражений формулою

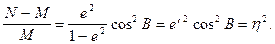
Величина h² характеризує відступ форми еліпсоїда в околицях даної точки від сфери.

Досить часто застосовуються і інші вирази для радіусів М та N

(2.42)

Дата добавления: 2014-01-04