Плоское движение твердых тел

Задачи

1. Уравнение зависимости угла поворота якоря тягового двигателя от времени имеет вид . Передаточное отношение редуктора 4,2, диаметр колеса 1,18 м. Определить зависимость скорости и ускорения поезда от времени.

2. Локомотив движется с ускорением 0,1 м/с². Определить угловое ускорение якоря тягового двигателя. Передаточное отношение редуктора 4,2, диаметр колеса 1,18 м.

3. Момент электромагнитных сил, действующих на якорь тягового двигателя, установленного на стенде, равен 400 Н·м. С каким угловым ускорением вращается якорь? Якорь считать цилиндром радиусом 0,25 м и массой 500 кг.

4. На шкив тягового двигателя, установленного на стенде, надет приводной ремень. Силы натяжения ветвей ремня равны 100 Н и 200 Н. Определить момент сил и мощность двигателя при частоте вращения 1200 об/мин, если диаметр шкива 0,20 м.

5. При трогаии поезда одна колесная пара буксовала в течении 3 с и достигла скорости вращения 3 об/с. Определить момент сил, действующих на колесо со стороны электродвигателя. Коэффициент трения скольжения 0,15, сила давления колеса на рельс 100 кН, момент инерции колесной пары 500 кг м².

6. Колесная пара на кг·м²стенде приводится во вращение электродвигателем с угловым ускорением 0,04 1/с². Определить вращающий момент сил якоря электродвигателя, если момент инерции колесной пары 500 кг·м², момент инерции якоря 100 кг·м². Передаточное отношение зубчатой передачи 4,5 (рис. 1).

7. Колесная пара, с моментом инерции 600 кг·м² на стенде вращается с угловой скоростью 100 1/с. Определить угловое ускорение под действием сил трения тормозных колодок, прижатых с силой 500 Н. Коэффициент трения скольжения 0,18. Определить число оборотов до остановки.

10. ДИНАМИКА ПЛОСКОГО ДВИЖЕНИЯ ТЕЛ

Плоскимявляется движение, при котором траектории точек тела лежат в параллельных плоскостях.

1. Движение центра масс

Центр масс твердого тела это точка, к которой приложена результирующая сила инерции при поступательном движении неинерциальной системы отсчета. В этом случае силы инерции, действующие на тела (или части тела), являются параллельными силами. Точно также параллельны в однородном поле тяжести силы тяжести, действующие на частицы тела. В этом случае положение центра масс и положение центра тяжести тела совпадают.

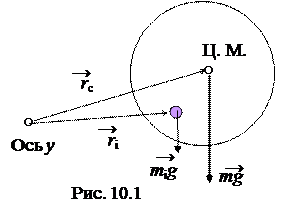Выведем формулу радиус-вектора центра тяжести. Потребуем, чтобы момент результирующей силы тяжести относительно некоторой оси y был бы равен векторной сумме моментов сил тяжести всех частиц тела относительно этой же оси (рис. 10.1).

Отсюда радиус-вектор центра тяжести или центра масс относительно выбранной оси можно определить по формуле

. (10.1)

Здесь m – суммарная масса тел. Проецируя это равенство на оси координат, можно определить три координаты центра масс.

Перенесем массу тела в левую часть уравнения и дважды продифференцируем по времени. Вторая производная это ускорение. В результате получим 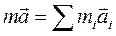. Произведение массы частицы на её ускорение равно действующей на частицу силе, а их сумма равна равнодействующей силе. Таким образом, центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, к которой приложены все внешние силы,

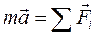. (10.2)

Отсюда следует, что если тело движется поступательно, то его можно принимать за материальную точку.

Пусть к телу, как будто плавающему на поверхности воды, в некоторой точке приложена сила F ₀ (рис. 10.2). Мысленно приложим к особой точке тела, называемой центром масс, две равные и противоположные силы F ₁ и F ₂, параллельные и равные силе F ₀. Под действием силы F ₂, тело совершает поступательное движение. А пара сил F ₀ и F ₁ создает момент сил M ₀ =F ₀ d, под действием которого тело вращается.

Итак, плоское движение тела можно представить как сумму двух движений: поступательного со скоростью центра масс и вращения вокруг оси, проходящей через центр масс под действием результирующей пар сил.

Возможно другое представление плоского движения. Пусть скорость точки О – центра масс тела равна (рис. 10.2). Проведём в плоскости движения перпендикуляр АОС к вектору скорости V ₀. Так как тело твёрдое, то огибающая линия концов векторов скоростей точек является прямой линией. Она и перпендикуляр пересекутся в некоторой точке С, скорость которой равна нулю. Через неё проходит так называемая мгновенная ось вращения, относительно которой тело совершает только вращательное движение с угловой скоростью . Положение мгновенной оси со временем меняется.

Примером плоского движения является качение колеса по рельсу. Если проскальзывания нет, то мгновенная ось вращения совпадает с линией касания колесной пары с рельсами, и перемещается со скоростью вагона.

Соответственно двум способам представления плоское движение может быть описано: либо уравнением основного закона динамики вращательного движения относительно мгновенной оси

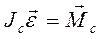, (10.3)

либо системой двух уравнений: второго закона Ньютона для поступательного движения тела как материальной точки, расположенной в центре масс, и основного закона динамики вращательного движения тела относительно оси, проходящей через центр масс

и (10.4)

В уравнениях J ₀ и J_с – моменты инерции тела относительно выбранных осей вращения О или С. Соотношение между моментами инерции тела относительно осей О или С определяют по теореме Штейнера.

Дата добавления: 2014-01-04