Основы релятивистской механики

1. Уравнение динамики

Уравнение второго закона Ньютона в классической механике инвариантно, не изменяет вида, при переходе от одной инерциальной системы отсчета к другой. Действительно, стоит в уравнение второго закона 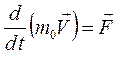подставить преобразования Галилея 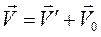, при постоянной скорости V ₀, при t=t^′, как получим инвариантное уравнение 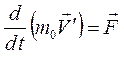. (Здесь введен индекс «ноль» для обозначения массы тела при малой скорости движения). Но в релятивистской механике преобразования Галилея неверны, следовательно, уравнение второго закона Ньютона следует преобразовать.

Если в классическом определении импульса 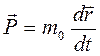заменить время собственным временем частицы, получим, что релятивистский импуль с определяется соотношением

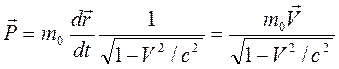. (13.7)

Основной закон релятивистской динамики материальной точки записывается так же, как и второй закон Ньютона 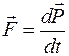, но только под 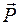понимается релятивистский импульс частицы (13.7). Следовательно, основное уравнение динамики принимает вид

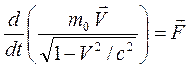. (13.8)

Так как релятивистский импульс не пропорционален скорости частицы, то ускорение 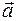и сила 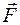оказываются не пропорциональными друг другу, не коллинеарными векторами.

Лоренц, при изучении движения электрона с учетом создаваемого им электромагнитного поля, получил, что его масса возрастает с увеличением скорости

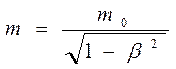. (13.9)

Причиной этого являлось увеличение инертности электрона из-за возникающего электромагнитного поля, которое по правилу Ленца тормозит движение электрона. Уравнение (13.9) проверено экспериментально по отклонению релятивистских электронов в поперечных электрических и магнитных полях, применяется при расчетах движения заряженных частиц в синхрофазотроне. При приближении скорости частиц к скорости света их масса беспредельно возрастает. Превысить скорость света невозможно.

2. Релятивистское выражение для энергии

В релятивистской механике обязан выполняться закон сохранения энергии.

Получим формулу кинетической энергии. Кинетическая энергия тела определяется через работу внешней силы Т=A, необходимую для сообщения телу заданной скорости. Чтобы разогнать частицу массы m ₀ из состояния покоя до скорости V под действием постоянной силы F, эта сила должна совершить работу

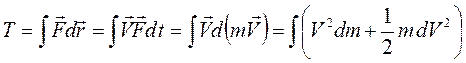. (13.10)

Здесь 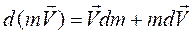. Под знаком интеграла стоят две переменные: масса и скорость. Исключим скорость по уравнению зависимости массы от скорости (13.9), возведя его во вторую степень 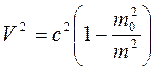и затем, дифференцируя квадрат скорости, 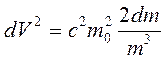. Подставим преобразования под знак интеграла кинетической энергии 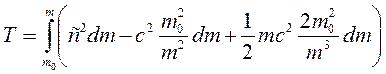. Видно, что два последних члена сокращаются. После интегрирования в пределах от массы покоя до релятивистской массы 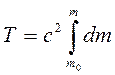, получим

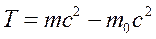. (13.11)

Эйнштейн интерпретировал первый член этого выражения как полную энергию Е движущейся частицы 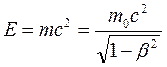. Неподвижная частица обладает энергией 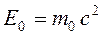, которая называется энергией покоя. Она представляет собой внутреннюю энергию частицы.

Закон пропорциональности массы и энергии является одним из самых важных выводов СТО. Масса и энергия являются различными свойствами материи. Масса тела характеризует его инертность, а также способность тела вступать в гравитационное взаимодействие с другими телами. Важнейшим свойством энергии является ее способность превращаться из одной формы в другую в эквивалентных количествах при различных физических процессах – в этом заключается содержание закона сохранения энергии. Пропорциональность массы и энергии является выражением внутренней сущности материи. Формула Эйнштейна

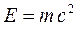(13.12)

выражает фундаментальный закон природы, который принято называть законом взаимосвязи массы и энергии.

Закон экспериментально подтвержден для ядерных реакций, в которых происходит значительное выделение энергии 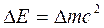, так что изменение массы можно измерить с высокой точностью. В реакции аннигиляции электрона и его античастицы позитрона с образованием фотонов происходит не только превращения энергии одного вида (энергия покоя) в другой (энергия движения), но и изменяется форма существования материи: вещество превращается в электромагнитное поле. Обратная реакция распада γ-фотона в электрон-позитронную пару происходит только при энергии фотона не менее 1,02 МэВ, равной энергии покоя частиц.

Найдем выражение для полной энергии через импульс частицы. Для этого из выражения для импульса (13.6) и полной энергии (13.8) исключим скорость V. В результате получим

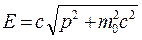(13.13)

Полученное соотношение (13.13) показывает, что частица может иметь энергию и импульс, но не иметь массы (m =0). Для таких частиц связь между энергией и импульсом выражается простым соотношением Е=рс. К частицам без массы покоя относятся фотоны и, возможно, нейтрино. Фотон – это электромагнитная волна, излученная атомом и, естественно, что волна не может покоиться. Во всех инерциальных системах отсчета они движутся с предельной скоростью с.

Дата добавления: 2014-01-04