Условия на границе двух диэлектриков

Рассмотрим границу двух диэлектриков с проницаемостями e₁ и e₂ соответственно (рис. 5.11.).

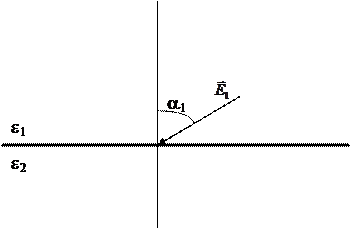
Рис. 5.11.

Напряжённость электрического поля в первой среде — . Направление этого вектора задано углом a₁ относительно нормали к границе раздела сред.

Определим величину и направление поля во второй среде — .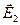

1. Воспользуемся теоремой о циркуляции электрического поля:

.

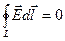Выберем на границе раздела сред замкнутый прямоугольный контур длины l и ширины D (рис. 5.12.). Частично этот контур проходит в первой среде, а частично — во второй. Циркуляция вектора напряжённости электрического поля по этому контуру равна нулю.

.

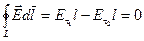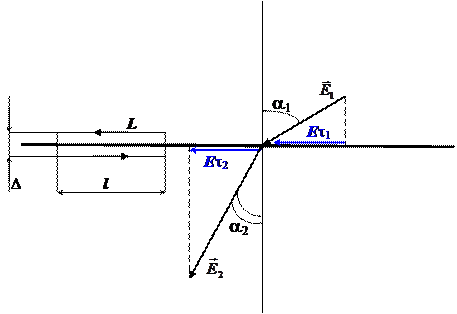
Рис. 5.12.

Здесь мы учли, что вклад в циркуляцию участков D стремится к нулю, при стремящейся к нулю ширине контура D. Отсюда следует, что:

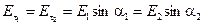. (5.17)

При переходе через границу раздела сред, касательная составляющая вектора напряжённости не меняется.

Для того чтобы выяснить, как меняется нормальная составляющая вектора напряжённости на границе сред, воспользуемся теоремой Остроградского-Гаусса (рис. 5.13.). Выберем на границе сред замкнутую цилиндрическую поверхность высоты h и с основаниями S ₁ = S ₂ = S, лежащими по разные стороны границы раздела диэлектриков. Согласно теореме Остроградского-Гаусса:

.

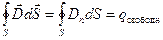Рис. 5.13.

Но по условию свободные заряды на границе раздела сред отсутствуют: q _{свободн} = 0, поэтому:

.

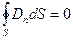Устремляя высоту цилиндра h к нулю, придём к выводу, что к нулю будет стремиться и поток вектора электрической индукции через боковую поверхность цилиндра. Искомый поток будет складываться только из потоков через основания:

;

;

.

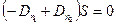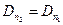Но D = ee₀ E. Следовательно:

.

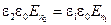Таким образом, нормальная составляющая вектора напряжённости электрического поля во второй среде равна:

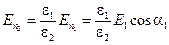. (5.18)

Теперь, зная составляющие вектора :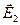

(5.17): ;

(5.18):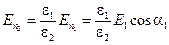

нетрудно найти и величину самого вектора:

.

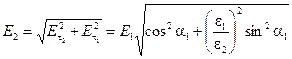Угол a₂, который вектор напряжённости поля образует во второй среде с нормалью к границе раздела диэлектриков, найдём, разделив уравнения (5.17) и (5.18):

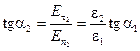. (5.19)

Уравнение (5.19) представляет собой закон преломления линий напряжённости электрического поля на границе раздела двух диэлектрических сред.

Лекция 6 «Постоянный электрический ток»

План лекции

1. Электрический ток. Характеристики электрического тока

2. Законы Ома для участка цепи

2.1. Закон Ома в интегральной форме

2.2. Закон Ома в дифференциальной форме

3. Пример расчёта силы тока в проводящей среде

4. Закон Джоуля-Ленца в дифференциальной и интегральной формах

Дата добавления: 2014-01-04