Формула де Бройля

Элементы квантовой механики

Выяснилось, что излучение обладает двойственной природой света. Наряду с такими свойствами света, как интерференция и дифракция, которые свидетельствуют о его волновой природе имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу: фотоэффект, эффект Комптона.

Несмотря на то, что излучение обладает такой двойственной природой, оно никогда не проявляет обоих своих качеств в условиях одного и того же опыта.

В каждом данном опыте оно ведет себя либо как волна, либо как частица.

В 1924 году Луи де Бройль выдвинул гипотезу, что этот двойственный характер присущ не только излучению, но он характерен и для всех материальных частиц.

По этой гипотезе с электронами, протонами, атомами и молекулами должен быть связан некоторый тип волнового движения.

Де Бройль пришел к этой гипотезе из рассмотрения положений специальной теории относительности и квантовой теории

Из теории вероятности следует, что энергия фотона , отсюда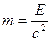

Из квантовой теории известно, что энергия фотона , импульс фотона P=mc

Полагая получим 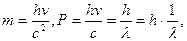где

- волновое число = k, причем можно считать, что k – вектор, совпадающий с направлением световых волн длиной .

Де Бройл перенес эти представления в динамику частицы. Согласно гипотезе де Бройля длина волны частицы связана с импульсом частицы соотношением 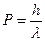, учитывая m – масса, 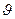- скорость P=m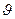

для любой частицы, движение частицы определяется особыми волнами, которые были названы волнами де Бройля.

Существование этих волн обнаружено экспериментально Девиссоном, Джермером и Томсоном. Длина волны, связанная с любой частицей массы m, движущейся со скоростью 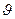будет

Если эта частица электрон, который приобрел свою скорость 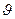под действием разности потенциалов U, то его кинетическая энергия (в случае, если скорость 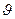мала по сравнению со скоростью света c) будет , a

Длина волны, связанная с ним, может быть представлена в виде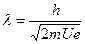

Например, для разности потенциалов в 100 В = 0,12 мм = 0,12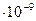м.

Эта длина волны имеет порядок расстояний между атомными плоскостями в кристаллах, значит возможно экспериментально доказать существование этих волн

В 1927 году Девиссон и Джеемер исследовали отражение электронов от монокристалла никеля. Они показали, что при рассеянии электронов от поверхности монокристалла никеля получается отчетливая дифракционная картина. Оказалось, что дифракционные максимумы соответствовали формуле Вульфа-Брэггов

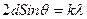, найденная длина волны = 0,165 мм соответствовала де Бройлевской длине волны, вычисленной при ускоряющей разности потенциалов U = 54B. При этом =0,167 мм, что подтверждает, что волновые свойства присущи не только потоку электронов, но и каждому электрону в отдельности.

Дифракция пучка электронов при прохождении через тонкие слои различных металлов была обнаружена Д.Томсоном и П. Тартаковским. Позднее было доказано, что не только электроны, но и протоны и нейтроны и даже молекулы водорода обладают волновыми свойствами, т.е. при их попадании на кристалл то же обнаруживается явление дифракции. В.А. Фабрикант доказал, что не только потоку частиц, но и каждому отдельному электрону присущи волновые свойства.

В настоящее время опыты по дифракции электронов и нейтронов и основанные на них приборы получили широкое распространение в науке и технике.

Дифракция электронов применяется при исследовании структуры поверхности (метод электронографии). Электрон сильно взаимодействуюет с веществом, поэтому проникающая способность электронов много меньше чем у рентгеновских лучей, что и делает электронографию особенно ценной при исследованиях структур поверхностей. Дифракция нейтронов используется в нейтронографии для изучения структур, особенно органических кристаллов, содержащих водород.

Нейтроны сильно взаимодействуют с веществом и дают эффективную картину дифракции. Открытие волновых свойств электронов вызвало появление новой отрасли науки электронной оптики. Волны де Бройля в принципе сопутствуют движению и любых макроскопических тел. Однако эти волны настолько малы. Их длина волны лежит за пределами доступной для наблюдения области. Например, для теннисного мяча с массой 100 г и летящего со скоростью 20 м/с .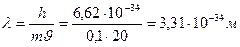

Поэтому считают, что макроскопические тела проявляют только одну сторону своих свойств – корпускулярную и не проявляют волновую.

Дата добавления: 2014-01-04