Квантование энергии свободных электронов в металлах

Основные положения квантовой теории металлов.

Элементы квантовой теории металлов.

Квантовая теория металлов, созданная в 20х годах прошлого столетия Френкелем (СССР) и Зоммерфельдом. На основе идей квантовой механики учитывает специфические свойства свободных электронов.

В основе квантовой теории металлов лежат принципиально новые идеи.

1) Идея о двойственной корпускулярно-волновой природе электронов.

Движение электрона в пространстве следует представить как процесс распространения своеобразной электронной волны, способной к интерференци, дифракции. Но понятие траектории не применимо.

Невозможно так же одновременно и точно определение положения электрона и его скорости.

2) Идея о дискретности

Энергия свободных электронов в металле может принимать не любые, а только некоторые дискретные значения, причём изменения могут происходить не непрерывно, а скачком.

3) Идея о неразличимости электронов в металле. Свободные электроны подчиняются не классической, статике Максвелла-Больцмана, в которой каждую частицу можно зафиксировать, а квантовой статистике Ферми-Дирака.

4) Важное значение для квантовой теории металлов имеет принцип Паули.

По квантовой теории состояние электрона как в изолированном атоме, так и в кристалле определяется набором четырёх квантовых чисел.

Согласно принципу Паули в атоме, молекуле, кристалле не может быть двух электронов, находящихся в тождественных квантовых состояниях, т.е. состояниях, определяемых одинаковым набором квантовых чисел.

1. Для понимания физических явлений, происходящих в металлах необходимо знать: Распределение свободных электронов в металле по энергетическим состояниям.

2. Полная энергия любого свободного электрона в металле складывается из потенциальной и кинетической энергии.

3. Металл представляет для свободных электронов своеобразную потенциальную яму с крутыми стенками.

Ход потенциальной энергии

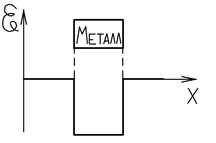
4. На велечину потенциальной энергии электронов в металле существенное влияние оказывает избыточный заряд, сообщённый металлу извне.

а) Если металл получает положительный заряд потенциальная энергия электронов уменьшается (дно потенциальной ямы опускается)

б) Если металл получает отрицательный заряд потенциальная энергия электронов увеличивается (дно ямы поднимается выше).

а) б)

5. Кинетическая энергия электронов как в изолированном атоме, так и в твёрдом теле квантуется: она может принимать лишь некоторые дискретные значения разделённые интервалами запрещённых значений.

Разрешённые значения энергии (их называют энергетическими уровнями) двух одинаковых невзаимодействующих атомов в точности совпадают.

6. При образовании из отдельных атомов кристаллического тела, атомы сближаются на столь малые расстояния, что их электронные оболочки перекрываются. Между атомами возникает взаимодействие, которое приводит к смещению энергетических уровней. В результате вместо одно уровня, образуется N уровней, то есть зона разрешённых энергетических уровней.

Упрощённая модель кристалла может быть представленна как цепочка прямоугольных потенциальных ям, разделённых потенциальными барьерами одинаковой толщины.

В результате Туннельного эффекта валентные ℮ˉ электроны перемещаются по кристаллу от атома к атому без изменения энергии, внутренние ℮ˉ связаны с конкретными атомами.

Движение электронов носит волновой характер поэтому просачивание сквозь барьер можно представить: из соотношения неопределённости Гейзенберга

∆Е·∆t≥ћ,

∆t – время нахождения электронов в энергетическом состоянии с энергией Е до Е+∆Е

В изолированном состоянии(не возбуждённом) в возбуждённом состоянии ∆t≈10ˉс, поэтому ∆Е≥h/∆t=10ˉэВ; в кристалле же ширина энергетического уровня ∆Е1≥h/∆t1~1эВ

Отсюда следует,что энергетический уровень электрона при образовании кристалла из отдельных атомов превращается в энергетическую зону, т.е. энергетический спектр ℮ˉ в твёрдом теле превращается в зонный спектр.

Расстояние между соседними уровнями мало 10ˉ²²-10ˉ²³ эВ

Расстояние – это разность энергий соседних энергетических уровней.

В любом твёрдом теле зоны разрешённых значений энергии разделены зонами запрещённых значений энергии, которые электрон, движущийся в кристалле иметь не может.

7. Заполнение разрешённых энергетических уровней в кристаллическом теле происходит в соответствии с принципом Паули.

Функция распределения Ферми и её статистический смысл.

Рассмотрим как распределяются в металле свободные электроны, по энергетическим состояниям электроны являются фермионами.

Закон распределения электронов по энергиям в металле был найден Ферми и Дираком.

Вводится функция распределения Ферми

где - энерия уровня; - химический потенциал или энергия Ферми; - постоянная Больцмана; - абсолютная температура.

Функция распределения Ферми вырастает в математическую вероятность того, что энергетический уровень при данной температуре занят электронами, т.е. показывает распределение электронов по состояниям и показывает кол-во электронов находящихся в квантовом состоянии с энергией .

Каждый энергетический уровень отвечает определённому значению энергии. Согласно принципу Паули на каждом разрешённом энергетическом уровне могут находиться 2 электрона, обладающие противоположными спинами.

Разрешённая зона, возникшая из уровня, на котором находятся валентные электроны в основном состоянии атома называется валентной зоной.

Частичное заполнение валентной зоны (а в металле её называют зоной проводимости) наблюдается в тех случаях, когда на последнем занятом уровне в атоме находится только один электрон или когда имеет место перекрывание зон. Зоной проводимости называется эта зона потому, что в отсутствии внешних возбуждений в ней нет электронов, а когда в эту зону перейдёт электрон, получив необходимую энергию, то сможет в этой зоне свободно изменять свою энергию, участвовать в проводимости.

Ширина энергетической зоны не зависит от размеров кристалла, а зависит от его строения, а количество энергетических уровней в зоне равно числу атомов в кристалле.

1) При абсолютном нуле T=0 все уровни с энергией, меньшей энергии Ферми, заняты электронами.

Все уровни, энергия которых больше энергии Ферми свободны. Энергия Ферми равна кинетической энергии электронов на этом уровне.

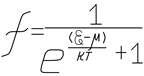
2) При T=0

Если =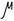, то

где - энергия уровня; - энергия Ферми.

При температуре, отличной от нуля уровень Ферми совпадает с тем разрешённым уровнем, вероятность заполнения которого равна ½. Т.е. энергия Ферми не является верхней границей заполненных уровней и энергия Ферми не равна максимальной кинетической энергии.

Энергия Ферми не зависит ни от конкретной формы, ни от объёма данного образца металла. Она зависит лишь от того, насколько плотно упакованы свободные электроны.

Величина этой энергии равна:

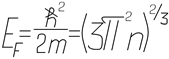где h – концентрация электронов проводимости.

Энергия отсчитывается от уровня Ферми

Важную роль играет валентная зона, образовавшаяся в результате расщепления самого верхнего занятого уровня.

Для металлов валентная зона заполнена не полностью.

Электроны, заполняющие в металле валентную зону, могут переходить с одного энергетического уровня на другой. Для этого необходимо:

1. Чтобы уровень был свободен.

2. Чтобы электрон получил добавочную энергию равную разности энергий того уровня, на который электрон переходит, с уровня, который он в данный момент занимает.

Дополнительную энергию электроны могут получать при нагревании металла за счёт энергии электрического поля.

Но если учесть, что переход электронов возник только вблизи уровня Ферми, то можно объяснить, что при повышении температуры, при нагревании металла средняя кинетическая энергия электронов мало меняется. Этим объясняется малый вклад электронного газа в теплоёмкость металла.

Что же касается теплопроводности металлов, то можно утверждать, что под действием электрического поля изменяют свою энергию только те электроны, которые находятся вблизи уровня Ферми.

Металлы, диэлектрики, полупроводники.

1) В зависимости от степени заполнения валентной зоны электронами;

2) Ширины запрещенной зоны возможны четыре случая:

1) Электроны заполняют валентную зону не полностью. Поэтому достаточно сообщить электронам, находящимся на верхних уровнях небольшую энергию ~10^-23 В достаточную, чтобы перевести их на более верхний уровень.

2)Частичное заполнение валентной зоны или в случае перекрытия валентной и свободной зоны электроны частично заполняют уровни свободной зоны.

Это указывает на то, что тело всегда будет проводником электрического тока. Это свойственно металлам.

В случае3 и 4 уровни валентной зоны полностью заполнены. Уровни свободной зоны или зоны проводимости не содержат электронов. Такие тела являются либо полупроводниками, либо диэлектриками.

Для переброса электронов в зону проводимости необходимо сообщить такую энергию, чтобы её величина была достаточной для перехода электронов из валентной зоны в зону проводимости т.е. не менее ∆ Е.

Если ширина запрещенной зоны ∆ Е>1 порядка нескольких эВ, то энергия теплового движения не достаточна для перевода электронов в свободную зону. В этом случае кристалл окажется изолятором.

Если ширина запрещенной зоны ∆ Е<1эВ, переброс электронов осуществляется довольно легко и тогда электроны, попавшие в верхнюю зону будет вести себя аналогично валентным электронам в металле. Свободная зона для них окажется зоной проводимости.

Значит различие металлов и диэлектриков с точки зрения данной теории состоит в том, что при 0^о К в зоне проводимости металлов имеются электроны, а в зоне проводимости диэлектриков их нет.

Различие же п∕п и диэлектриков определяется шириной запрещенной зоны. Для п∕п ширина запрещенной зоны узка. Для диэлектриков она довольно широка. При температурах, близких к 0^о К п∕п ведут себя как диэлектрики, т.к. переброса электронов в зону проводимости не происходит.

С повышением температуры у п∕п растёт число электронов, которые в следствие теплового возбуждения переходят в зону проводимости, т.е.электрическая проводимость п∕п увеличивается.

П∕п по величине электропроводности занимают промежуточное положение между проводниками т.е. металлами и диэлектриками.

Различают собственные и примесные п∕п и соответственно собственную и примесную проводимость. К числу собственных относятся химически чистые п∕п, и их проводимость называется собственной (германий, селен, СdS и т.д.) При 0^о К и в отсутствии других внешних факторов собственные п∕п ведут себя как диэлектрики при повышении же температуры электроны с верхних уровней валентной зоны могут быть переброшены на нижние уровни зоны проводимости.

При наложении на кристалл электрического поля эти электроны перемещаются против поля и создают эл.ток.Проводимость собственных п∕п, обуславливается электронами называется электронной проводимостью или проводимостью n-типа (негативно-отрицательные).

В результате переброса электронов из валентной зоны в зону проводимости в валентной зоне возникают валентные состояния дырки.

На освободившееся место (дырку) может переместиться электрон с соседнего уровня, а дырка появится в том месте откуда ушёл электрон и т.д. Такой процесс замещения дырок электронами равносилен перемещению дырки в противоположном направлении, чем электрон, т.е. как бы дырка обладает положительным зарядом. Проводимость собственных п∕п обуславливается квазичастицами- дырками, называется дырочной проводимостью p-типа (позитив-положительными).

Значит в собственных п∕п наблюдается 2-а механизма проводимости:

Электронный и Дырочный

Число электронов равно числу дырок т.е. концентрации электронов проводимости и дырок равны: n_e = n_p.

Проводимость п∕п всегда проявляется только под действием внешних факторов (t, облучения, сильные поля) Для примера возьмём кремний.

Si- кристалл, каждый атом которого окружен четырьмя ближайшими соседями и связан с ними ковалентной связью:

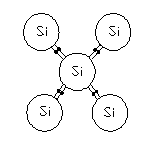
Т=0

При T=0 все связи заполнены, все уровне валентной зоны заняты электронами, все уровни зоны проводимости свободны.

Для того, чтобы вырвать электрон из связи, электрон нужно возбудить, т.е. сообщить ему определенную энергию. Эта энергия называется энергией ионизации атомов или энергией активации носителей.

Для примера рассмотрим термическое возбуждение:

Т≠0

Электрон в результате теплового возбуждения разрываетсвязь и становится свободным. Образовавшееся пустое место – дырка.

Если вблизи дырки оказывается свободный электрон, то он может занять её место и связь будет восстановлена. Этот процесс превращения свободного электрона в связанный называется рекомбинацией электрона и дырки. (процесс исчезновения полезных носителей)

Этот процесс соответствует переходу электрона из валентной зоны на свободный уровень зоны проводимости. При таком переходе освобождается энергия, которая передаётся решетке или испускается в виде кванта света. Но если дырка захватывает электрон из валентной зоны, то дырка появляется в другом месте, на месте захваченного электрона, этот процесс можно представить как движение одной и той же дырки, т.е. положительного заряда e⁺.

Тепловому движению дырок в валентной зоне соответствует хаотическое движение электронов связи, тепловому движению электронов в зоне проводимости соответствует хаотическое движение свободных электронов.

При создании в п/п электрического поля электроны будут двигаться против поля е^-дырки будут двигаться по полю е⁺¹ электроны поднимаются вверх, дырки опускаются вниз.

Количество электронов переброшенных в зону проводимости и образовавшихся дырок пропорционально.

Энергия Ферми в собственном п/п представляет собой энергию, от которой происходит возбуждение электронов и дырок. Так как энергия, идущая на переброс электронов и затрачивается на образование дырок одинаковая, от уровень Ферми должен находиться в середине запрещенной зоны, а удельная проводимость 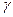равна:

где постоянная характерная для данного п/п.

Увеличение проводимости п/п с повышением температуры является их характерной особенностью (у металлов проводимость уменьшается) Т.е. с повышением температуры растёт число электронов, которые переходят в зону проводимости и участвуют в проводимости, поэтому удельная проводимость собственных п/п с повышением температуры растёт, прологарифмируем:

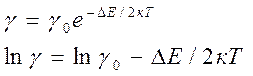
Если представить зависимость ln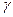от 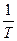, то это прямая:

по наклону которой можно определить , ширину запрещенной зоны, а по её продолжению , где к- постоянная Больцмана.

Примесная проводимость п/п

Рассмотрим пример, если в кристалле атомы кремния Si будут частично заменены примесными атомами элемента V группы периодической системы (As) мышьяк имеющим 5 валентных электронов, 4- валентных электрона заполнят валентные связи с четырьмя соседними атомами, а пятый окажется «лишним».

Он не принимает участия в образовании химических связей, поэтому он слабее других электронов связан со своим атомом.

При Т=0 этот электрон локализован около своего атома и занимает отдельный энергетический уровень, который расположен чуть ниже дна зоны проводимости в запрещенной зоне.

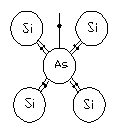
Для отрыва этого электрона нужно затратить чтобы вырвать электрон из ковалентной связи.

энергия активации приместных носителей заряда. Для атомов мышьяка и кремния 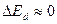, 0,8 В. Вероятность перехода электрона с этого уровня пропорциональна ,поэтому, чем выше температура, тем больше число электронов переходят с примесного уровня в зону проводимости. Такая проводимость называется электронной п/п электронным примеси, поставляющие электроны в зону проводимости называют донорными, а уровень донорным.

Акцепторные примеси Р- полупроводники.

Для примера в качестве примеси рассмотрим атом индия In у которого валентность равна 3-ем.

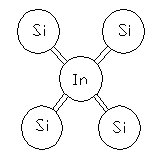
при Т=0 одна из связей оказывается неукомплектованной. Она представляет вакансию 0.

при Т≠0 атом In (индия может захватить не достающей электрон у одного из ближайших атомов Si (кремния).

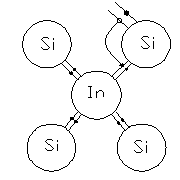
на месте разорванной связи образуется дырка.

этому соответствует переход электрона

из зоны валентной на свободный примесный

энергетический уровень.

Этот переход сопровождается поглощением

энергии.

В этом случае происходит образование дырок, п/п называются дырочными или р- полупроводниками, примеси захватывающие электроны называются акцепторами, а электрические уровни этих примесей акцепторными (принимающие) п/п можно отнести к р- или n- типу только тогда, когда дырки или электроны, создаваемые примесными атомами, являются основными носителями тока и их концентрация значительно больше собственных носителей заряда п/п расчёты показали, что при Т=0.

Уровень Ферми в п/п n – типа расположен посередине между донорным уровнем и дном зоны проводимости. Уровень Ферми в п/п р – типа посередине между акцепторным уровнем и потолком валентной зоны.

Контакт двух полупроводников с различным типом проводимости.

Полупроводниковый диод (р – n- переход)

Граница соприкосновения двух п/п имеющих электронную и дырочную проводимость называется электронно-дырочным переходом или р – n переходом. Эти переходы являются основой работы многих п/п приборов.

В n – полупроводнике основными носителями электрических зарядов являются электроны в зоне проводимости, не основными – дырки в валентной зоне.

В р – п/п - основными – дырки валентной зоне

- не основными – электроны в зоне проводимости.

Если электрический контакт между такими п/п отсутствует, то их электрические диаграммы имеют вид:

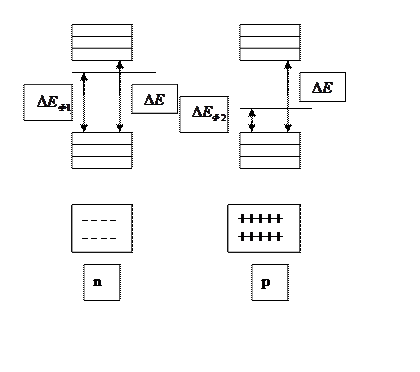
Уровень Ферми не совпадает - ширина запрещенной зоны одинакова, после того, как привести в контакт, например на кристалл германия n – типа накладывается индиевая таблетка. Система нагревается при t = 500^оС в вакууме. Атомы индия диффузируют на некоторую глубину в германий, затем расплав охлаждают.

Так как уровни Ферми первоначально не совпадают, электроны из n – п/п будут диффузировать в Р п/п диффузия дырок будет осуществляться в обратном направление.

Процесс преимущественного перехода электронов и дырок из п/п в п/п происходит до тех пор пока уровни Ферми в п/п сравняются.

В условиях равновесия между n и p - п/п устанавливается вполне определенная внутренняя контактная разность потенциалов .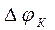

В области р-n- перехода энергетические зоны искривляются, появляются потенциальные барьеры как для электронов так и для дырок.

Высота потенциального барьера определяется первичной разностью положений уравней Ферми в обоих п/п.

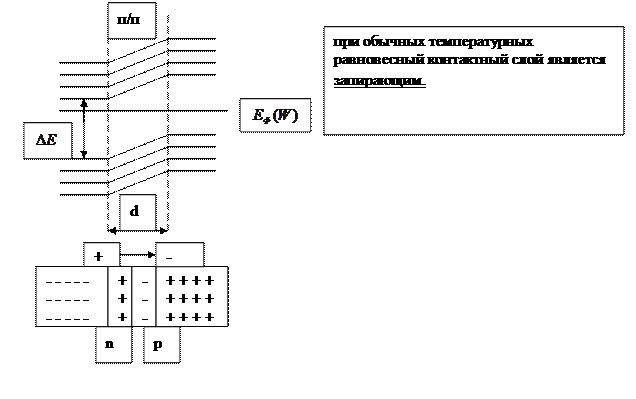
Сопротивление запирающего слоя можно изменить с помощью внешнего электрического поля. Если приложенное к р- n переходу внешнее электрическое поле направлено от n – п/п к р – п/п, то оно вызывает движение электронов и дырок от границы в противоположные стороны:

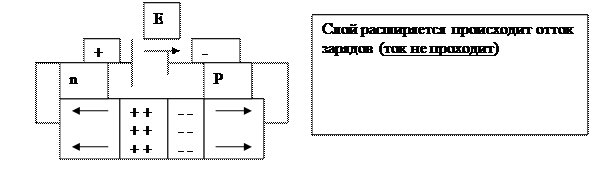
Если приложенное к р – n переходу внешнее поле направлено противоположно полю контактного слоя

Толщина слоя уменьшается р – n переход обладает односторонней вентильной проводимостью, (это явление положено в основу работы, Солнечных батарей.)

Этот переход обладает большой проводимостью в прямом направлении и большим сопротивлением в обратном направлении, что совпадает с действием лампового диода.

Вольт – амперная характеристика:

Триоды основаны на действии р – n перехода они представляют собой 2 n – p переход или

n – p – n

p – n - p

Полупроводниковые диоды

Полупроводниковый диод

Полупроводниковое устройство, содержащее один р-n-переход.

Дата добавления: 2014-01-04