Методы определения вязкости жидкости

Определение вязкости биологических жидкостей и, особенно, вяз­кости крови имеет существенное диагностическое значение. Разнооб­разные приборы, применяемые для этой цели, называют вискозиметрами.

а) Метод Стокса (метод падающего шарика).

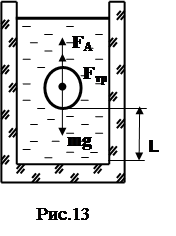Представим цилиндр, заполнен­ный жидкостью плотностью r_ж,вязкость которой h подле­жит определению (см.рис.13). Если в этой жидкости падает шарик радиусом r, массой m и плотностью r, то движение ша­рика определяется действую­щими на него тремя силами: силой тяжести F_т = mg, силой Архимеда F_А=4p r³r_ж g /3 и си­лой трения F_тр. Согласно за­кону Стокса, сила сопротив­ления движению шарика про­порциональна его радиусу, скорости движения и вязкости жидкости:

F_тр = 6 p h r v. (18)

Сила трения уменьшает скорость движения шарика и через неко­торое время после погружения шарика в жидкость его движение может стать равномерным. При достижении равномерного движения сила тя­жести становится равной сумме силы трения и силы Архимеда:

4/3p r ³r g = 4/3p r³r_жg + 6p h r v. (19)

Из уравнения (19) определим искомую вязкость:

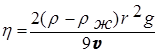. (20)

Таким образом, для нахождения вязкости жидкости необходимо знать ее плотность, а так же радиус и плотность шарика. Скорость движения шарика v определяется экспериментально. Для этого измеря­ется время t, за которое шарик равномерно проходит в жидкости расстояние L: v = L / t. Метод Стокса весьма прост (при необходимом условии равномерности движения шарика) и обладает хорошей точ­ностью. Однако, для определения вязкости крови он практически не применяется - хотя бы потому, что требует значительного количества исследуемой крови. Кроме того, в жидкостях, обладающих не очень большой вязкостью, сложно удовлетворить требованию равномерности движения шарика.

б) Капиллярные методы.

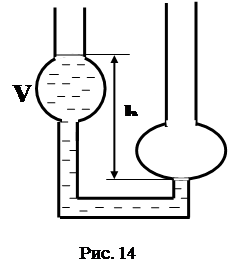Капиллярные методы, основаны на применении формулы Пуазейля (13). Рассмотрим, например, течение жидкости через капилляр в вискозиметре Остваьда. Представим U - образную трубку. В одном из ее плеч имеется небольшая полая сфера, объемом V, которая капилля­ром соединяется с резервуаром, расположенным в другом плече. Эта система заполняется жидкостью так, что разность ее уровней состав­ляет величину h (см.рис.14). Пусть вначале вискозиметр заполнен эталонной жидкостью, вязкость которой точно известна. В качестве такой жидкости удобно использовать дистиллированную воду.

Поскольку при засасыва­нии воды в левое плечо вис­козиметра ее уровень здесь выше, чем в правом, то после прекращения всасывания жид­кость будет перетекать че­рез капилляр из левого пле­ча вискозиметра в правое до наступления равенства уров­ней. С помощью секундомера легко определить время t_о, за которое вода вытекает из полости объемом V. Сог­ласно формуле (13) этот объем вытекшей воды равен:

V = t_о. (21)

В формуле (21) разница давлений определяется величиной r_о g h, где r_о - плотность воды, а h_о - табличное значение вязкости воды при данной температуре. Определив время истечения воды t_о, заполним вискозиметр исследуемой жидкостью, вязкость которой необ­ходимо определить. При этом необходимо обеспечить такую же раз­ность уровней жидкости h в плечах вискозиметра, что и при его за­полнении водой. Затем измеряем время t истечения объема исследуе­мой жидкости V, который определяется формулой:

V = , (22)

где h - вязкость исследуемой жидкости, а r - ее плотность.

Разделив выражение (21) на (22) получим:

1 = 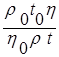. (23)

Таким образом, для определения вязкости исследуемой жидкости получаем формулу:

h = . (24)

Итак, при использовании этого метода необходимо знать плот­ности исследуемой жидкости и воды при данной температуре, таблич­ные значения вязкости воды и измерить лишь времена истечения.

Для определения вязкости проб крови может быть использован вискозиметр Гесса, в котором определяются не времена истечения жидкости из капилляра, а расстояния L_о и L, на которые перемещают­ся вода и кровь за одно и то же время. Применение выражения (13) для этого случая приводит к следующей расчетной формуле, определя­ющей вязкость крови h:

h =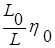. (25)

в) Ротационные методы.

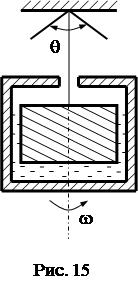Достоинством этих методов является возможность определять не только значение вязкости, но и ее зависимость от скорости сдвига: h = f (d v /dx). Существуют разнообразные ротационные вискозиметры. Рассмотрим принцип устройства одного из них. Представим два ци­линдра, имеющих общую ось вращения (рис.15). Внутренний цилиндр подвешен на нити, а внешний может вращаться вокруг своей продоль­ной оси с регулируемой угловой скоростью w. Зазор между цилиндрами заполняется исследуемой жидкостью, в частности, кровью. За счет вязкости жидкости при вращении наружного цилиндра внутренний цилиндр начинает пово­рачиваться, достигая равновесия при неко­тором угле поворота q. Этот угол можно легко измерить. Чем больше вязкость жид­кости и угловая скорость вращения w, тем больше и указанный угол поворота: q = k h w, где k - постоянная прибора. При разных значениях скорости w в жидкости, заполняю­щей зазор между цилиндрами, реализуются и различные градиенты скорости. Для ньютоно­вых жидкостей значение вязкости не зависит от градиента скорости (следовательно и от величины w), а в неньютоновских жидкостях эту зависимость можно не только наблюдать, но и определить количественно. Таким обра­зом, данные ротационной вискозиметрии позволяют судить об изменении вязкости движущейся крови при различных скоростях сдвига.

Дата добавления: 2014-01-04