Электрические токи в металлах, вакууме и газах

СРС

Элементарная классическая теория электропроводности металлов

Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристалличе­ской решетки металла. Это представление о природе носителей тока в металлах осно­вывается на электронной теории проводи­мости металлов, созданной немецким фи­зиком П. Друде (1863—1906) и разрабо­танной впоследствии нидерландским фи­зиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории.

Первый из таких опытов — опыт Рикке (1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндров (Сu, Аl, Сu) одинакового ради­уса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (»3,5•10⁶ Кл), ни­каких, даже микроскопических, следов пе­реноса вещества не обнаружилось. Это явилось экспериментальным доказательст­вом того, что ионы в металлах не участву­ют в переносе электричества, а перенос заряда в металлах осуществляется части­цами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856—1940) электроны. Для доказательства этого предполо­жения необходимо было определить знак и величину удельного заряда но­сителей (отношение заряда носителя к его массе). Идея подобных опытов за­ключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы дол­жны по инерции смещаться вперед, как

смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно опреде­лить знак носителей тока, а зная размеры и сопротивление проводника, можно вы­числить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат советским физи­кам С. Л. Мандельштаму (1879—1944) и Н. Д. Папалекси (1880—1947). Эти опыты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881 —1948) и ранее шотландским физиком Б. Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах заряжены отрицательно, а их удельный заряд приблизительно оди­наков для всех исследованных металлов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удель­ного заряда и массы носителей тока и электронов, движущихся в вакууме, со­впадали. Таким образом, было оконча­тельно доказано, что носителями электри­ческого тока в металлах являются свобод­ные электроны.

Существование свободных электронов в металлах можно объяснить следующим образом: при образовании кристалличе­ской решетки металла (в результате сбли­жения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от ато­мов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.

Электроны проводимости при своем движении сталкиваются с ионами решет­ки, в результате чего устанавливается тер-

модинамическое равновесие между элек­тронным газом и решеткой. По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и мо­лекулы одноатомного газа. Поэтому, при­меняя выводы молекулярно-кинетической теории (см. (44.3)), можно найти среднюю скорость теплового движения электронов

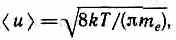
которая для T=300 К равна 1,1•10⁵ м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возник­новению тока.

При наложении внешнего электриче­ского поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Сред­нюю скорость <v> упорядоченного движе­ния электронов можно оценить согласно формуле (96.1) для плотности тока: j= ne<v>. Выбрав допустимую плотность тока, например для медных проводов 10⁷ А/м², получим, что при концентрации носителей тока n =8•10²⁸ м^-3 средняя скорость (v) упорядоченного движения электронов равна 7,8•10^-4 м/с. Следова­тельно, <v> << <u>, т. е. даже при очень больших плотностях тока средняя ско­рость упорядоченного движения электро­нов, обусловливающего электрический ток, значительно меньше их скорости теплово­го движения. Поэтому при вычислениях результирующую скорость (<v> +<u>) можно заменять скоростью теплового дви­жения <u>.

Казалось бы, полученный результат противоречит факту практически мгновен­ной передачи электрических сигналов на большие расстояния. Дело в том, что замыкание электрической цепи влечет за собой распространение электрического поля со скоростью с (с =3•10⁸ м/с). Через время t=l/c (l — длина цепи) вдоль цепи установится стационарное электри­ческое поле и в ней начнется упорядо­ченное движение электронов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыка­нием.

§ 103. Вывод основных законов электрического тока в классической теории электропроводности металлов

1. Закон Ома. Пусть в металлическом проводнике существует электрическое по­ле напряженностью Е= const. Co стороны поля заряд е испытывает действие силы F=eE и приобретает ускорение а=F/m=еЕ/т. Таким образом, во время сво­бодного пробега электроны движутся рав­ноускоренно, приобретая к концу свобод­ного пробега скорость

v_max= еE<t>.

где < t >—среднее время между двумя последовательными соударениями элек­трона с ионами решетки.

Согласно теории Друде, в конце сво­бодного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упо­рядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона

<v>=(v_max+0)/2= eE<t>/(2m). (103.1)

Классическая теория металлов не учи­тывает распределения электронов по ско­ростям, поэтому среднее время < t > сво­бодного пробега определяется средней длиной свободного пробега < l > и средней скоростью движения электронов относи­тельно кристаллической решетки провод­ника, равной <u>+(v) (< u > — средняя скорость теплового движения электронов). В §102 было показано, что (v)<< <u>, поэтому

<t>=< l >/<u>.

Подставив значение < t > в формулу (103.1), получим

<v>=eE< l >/(2m<u>).

Плотность тока в металлическом провод­нике, по (96.1),

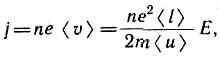
откуда видно, что плотность тока пропор­циональна напряженности поля,

т. е. получили закон Ома в дифференци­альной форме (ср. с (98.4)). Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость ма­териала

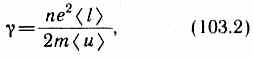
которая тем больше, чем больше концен­трация свободных электронов и средняя длина их свободного пробега.

2. Закон Джоуля — Ленца. К концу свободного пробега электрон под действи­ем поля приобретает дополнительную ки­нетическую энергию

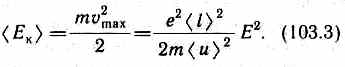
При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.

За единицу времени электрон испыты­вает с узлами решетки в среднем <z> столкновений:

<z>=<u>/<l>. (103.4)

Если n — концентрация электронов, то в единицу времени происходит n<z> стол­кновений и решетке передается энергия

w = n < z >< E _к>, (103.5)

которая идет на нагревание проводника. Подставив (103.3) и (103.4) в (103.5), получим таким образом энергию, переда­ваемую решетке в единице объема провод­ника за единицу времени,

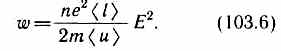
Величина w называется удельной тепловой мощностью тока (см. §99). Коэффициент пропорциональности между w и Е ² по (103.2) есть удельная проводимость g; сле­довательно, выражение (103.6) —закон Джоуля — Ленца в дифференциальной форме (ср. с (99.7)).

3. Закон Видемана — Франца. Метал­лы обладают как большой электропровод­ностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы — свободные электроны, кото­рые, перемещаясь в металле, переносят не только электрический заряд, но и прису­щую им энергию хаотического теплового движения, т. е. осуществляют перенос теплоты.

Видеманом и Францем в 1853 г. экспе­риментально установлен закон, согласно которому отношение теплопроводности (l) к удельной проводимости (g) для всех металлов при одной и той же температуре одинаково и увеличивается пропорцио­нально термодинамической температуре:

l/g=bT,

где b — постоянная, не зависящая от рода металла.

Элементарная классическая теория электропроводности металлов позволила найти значение b: b=3(k/e)², где k — пос­тоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным слу­чайно. Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов по скоростям, получил b = 2 (k/e) ², что привело к резкому расхождению теории с опытом.

Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Ви­демана — Франца. Однако она помимо рассмотренных противоречий в законе Ви­демана — Франца столкнулась еще с ря­дом трудностей при объяснении различных опытных данных. Рассмотрим некоторые из них.

Температурная зависимость сопротив­ления. Из формулы удельной проводимо­сти (103.2) следует, что сопротивление металлов, т. е. величина, обратно пропор­циональная g, должна возрастать пропор­ционально ÖT (в (103.2) n и < l > от темпе­ратуры не зависят, а < u > ~ÖТ). Этот вывод электронной теории противоречит опытным данным, согласно которым R~T (см. §98).

Оценка средней длины свободного про­бега электронов в металлах. Чтобы по формуле (103.2) получить g, совпадающие с опытными значениями, надо принимать < l > значительно больше истинных, иными словами, предполагать, что электрон про­ходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемко­сти электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость ди­электриков, у которых нет свободных элек­тронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3 R. Учтем, что теплоем­кость одноатомного электронного газа равна ³/₂ R. Тогда атомная теплоемкость металлов должна быть близка к 4,5 R. Однако опыт доказывает, что она равна 3 R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электрон­ной теорией.

Указанные расхождения теории с опы­том можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а зако­нам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. По­этому объяснить затруднения элементар­ной классической теории электропровод­ности металлов можно лишь квантовой тео­рией, которая будет рассмотрена в даль­нейшем. Надо, однако, отметить, что клас­сическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводи­мости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой тео­рией простой и наглядной.

Дата добавления: 2014-01-04