Электростатика

1. Электр зарядының сақталу заңы. Кез келген дене атомдар мен молекулалардан, ал атомдар элементар бөлшектерден тұрады. Атом қрамына кіретін протон мен электрон электр зарядын тасымалдайды. Ал нейтронда заряд болмайды. Протон оң зарядты, ал электрон теріс зарядты болып есептеледі. Бөлшектер өзін қоршаған ортаға түрліше әсер етіп, ортаның әсерінен өздері де түрліше қасиетке ие болады. Бөлшектерге сыртқы күшпен әсер етсек, олар массалары әртүрлі болғандықтан, әр түрлі қырынан көрінеді. Электрон мен протонның зарядталуы дегеніміз олар түрлі типтегі өзара әсерлесуге қабілетті деген ойды тұжырымдаймыз.

Сонымен заряд дегеніміз элементар бөлшектерді сипаттайтын, массадан кейінгі екінші қасиет.

Американ физигі Р.Милликен мен совет физигі А.Иоффе тәжірибелерінің қорытындысынан электр зарядының элементар заряд деп атауға болатынын тұжырымдады, яғни e=1,6×10^-19 Кл. Электронның массасы m_e=9,11×10^-31кг, ал протонның массасы m_e=1,67×10^-27кг.

Атом құрамындағы протондар мен электрондар саны бірдей болады. Демек, ондағы оң зарядтар мен теріс зарядтардың саны бірдей болады. Егер денедегі электрондар саны протондар санынан артық болса, онда дене теріс зарядталған, ал электрондар саны протондар санынан кем болса, онда дене оң зарядталған болады. Денедегі әр аттас зарядтардың жалпы саны өзгермейді: ол зарядтар тек денелер арасында өзара бөлінеді.

Тәжірибелер нәтижесінде ағылшын физигі М.Фарадей табиғаттың негізгі (фундаментальды) заңы–зарядтың сақталу заңын ашты: кез келген тұйық жүйенің электр зарядтарының алгебралық қосындысы осы жүйе ішінде қандай процестер өтсе, өзгермей қалады. Аттас зарядтар бірін-бірі тебеді, ал әр аттас зарядтар бірін-бірі тартады.

Нүктелік заряд дегеніміз-электрленген материалдық нүкте. Оның өлшемін онымен әсерлесетін басқа бір денеге дейінгі ара қашықтықпен салыстырғанда ескермеуге болады.

Денедегі еркін зарядтардың концентрациясына (шоғырына) байланысты олар өткізгіштер, диэлектриктер және жартылай өткізгіштер болып бөлінеді. Өткізгіштер- электр заряды бүкіл көлемі бойынша еркін қозғала алатын денелер. Өткізгіштер екі топқа бөлінеді: 1) бірінші текті өткізгіштер (металдар)-олардағы заряд қозғалысы химиялық өзгеріске ұшыратпайды; 2) екінші текті өткізгіштер (еріген тұздар, қышқыл ерітінділері)-оларда заряд (оң және теріс иондар) тасымалданғанда химиялық өзгеріске ұшырайды. Диэлектриктер (шыны, пласмасса) - еркін зарядтары болмайтын денелер. Жартылай өткізгіштер (германий, кремний) - өткізгіштер мен диэлеткриктердің аралығындағы заттар.

Электр зарядының өлшем бірлігі- кулон.

2. Кулон заңы. Вакуумдағы қозғалмайтын екі нүктелік электр зарядының өзара әсерлесу күшінің олардың ара қашықтығына тәуелділігі Кулон заңы арқылы тағайындалған. Кулон заңы электростатиканың негізгі заңы болып табылады.

Бір-бірінен l қашықтықта орналасқан екі нүктелік зарядтардың өзара әсерлесу күші сол зарядтардың көбейтіндісіне тура және олардың арақашықтығының квадратына кері пропорционал: F=k ½ q₁q₂ ½ /r² (9.1)

F күші өзара әсерлесетін зарядтарды қосатын түзу бойымен бағыттала-ды, мұндағы k -пропорционалдық коэффициент k=1/4pe_0,, мұндағы

e_0,- электр тұрақтысы, e₀= 8,85×10^-12 Кл²/(Н×м²).

Әр текті ортада зарядтардың әсерлесу күші әртүрлі болады. Ол ортаның диэлектрик өтімділігіне (e) байланысты. Ауа үшін e=1. Басқа орталар үшін e мәнін оқулықтарда берілетін кестелерден алуға болады. Диэлектрлік өтімділік зарядтардың вакуумдағы әсерлесу күшінің басқа ортадағы әсерлесу күшінен қанша есе кем екендігін білдіреді.

3. Электр өрісі. Өріс кернеулігі, потенциалы және жұмысы. Белгілі қашықтықта тұрған екі зарядтың әсерлесуі электр өрісінің көмегімен жүзеге асады. Электр өрісі-материяның ерекше түрі, оны қозғалмайтын электр заряды туғызады. Электр өрісі электрленген дененің әсерін екінші денеге жеткізуші орта болып саналады. Электр өрісінің пайда болғанын және оның интенсивтігін сол өріске орналастырылған сыншы зарядқа әсер ететін күш арқылы анықтауға болады. Сол күштің зарядқа қатынасына тең векторлық шама-электр өрісінің кернеулігі (Е) деп аталады: E=F/ q ₀ (9.2). Кернеуліктің өлшем бірлігі- В/м, бағыты оң зарядқа әсер ететін күш бағытына қарама-қарсы болады.

Потенциалдыөрісте (электростатикалық өріс–потенциалдық өріс деген болатынбыз) орналасқан дененің потенциалдық энергиясы болады, сол энергия есебінен өрісте күш жұмыс атқарады және консервативті күштердің жұмысы потенциалдық энергияның кемуімен жүзеге асады. Сондықтан электростатикалық өріс күштерінің жұмысын энергиялардың айырмасы түрінде көрсетуге болады: A=U₁-U₂ (9.3), сонда q₀ зарядтың q зарядтың өрісіндегі потенциалдық энергиясы U=kq₀q/r (9.4).

Осы формуладан j=U/q₀ (9.5) электростатикалық өрістің энергетикалық сипаттамасы болып табылады да, потенциал деп аталады. Электро-статикалық өрістің қандай да бір нүктесіндегі потенциал осы нүктедегі бірлік оң зарядтың потенциалдық энергиясымен анықталатын физикалық шама, өлшем бірлігі- вольт. (9.3) және (9.5) формулалардан нүктелік заряд тудырған өріс потенциалының формуласы шығады j=kq/r (9.6). Өрістің 1-нүктесінен 2-нүктесіне q₀ зарядты орын ауыстырғанда электроста-тикалық өріс күштерінің жұмысы 1-және 2-нүктенің потенциалдарының айырмасына тең болады A=q₀(j₁-j₂) (9.7)

4. Кернеулік векторының циркуляциясы. Электр өрісі кернеулігі мен потенциал арасындағы байланыс. Осыған байланысты Гаусс теоремасы шығады: тұйықталған бет арқылы өтетін кернеулік векторының ағыны осы бет ішіндегі зарядтардың алгебралық қосындысын e₀-ге бөлгенге тең: ò_s E d S =1/e₀Sq_i. (9.8)

Электростатикалық өріс–потенциалдық өріс, себебі q₀ зарядтың орын ауыстырғанда істеген жұмысы оның жолына ғана емес, осы зарядтың бастапқы және соңғы орнына да байланысты. Ал электростатикалық күштер консерватив күштер болып табылады. Сыртқы электростатикалық өрісте кез келген тұйықталған жол бойынша электр зарядын тасымал-дағанда жасалатын жұмыс нольге тең болады: (9.9)

Тұйық L контуры бойынша алынған интеграл Е векторының циркуляциясы деп аталады. Сөйтіп, электростатикалық өріске тән нәрсе-кез келген тұйық контур бойынша кернеулік векторының циркуляциясы нольге тең болады.

Потенциалдары тұрақты нүктелердің геометриялық орны потенциал деңгейінің беті немесе эквипотенциал бет деп аталады. Потенциал деңгейінің бетінде зарядты көшіру жұмысы нольге тең. Кернеулік пен потенциал арасындағы қатысты қарастыратын болсақ, электростатикалық өрістің керенулігі оның күштік қасиетін сипаттаса, өрістің потенциалы оның энергетикалық қасиетін көрсетеді. Потенциал скаляр шама болғандықтан, электр өрісін скаляр өріс ретінде қарастырады. Сол себепті скаляр градиенті деген ұғым енгізілген. Зарядтың өрістегі орын ауыстыру кезінде жасайтын жұмысы: dA=Fdr, немесе dA= -q^¢dj. Осы теңдеулерді теңестіреміз F/q^¢=-dj /dr, осындағы F/q^¢=Е, ал dj /dr-потенциал градиенті. Сонда Е=-dj /dr (9.10) болады. Сонымен, кернеулік сан жағынан алғанда деңгей бетіне перпендикуляр бағытпен есептелінген ұзындық бірлігіне келетін потенциалдың өзгерісіне тең болады да, потенциалдың кему жағына қарай бағытталады. Сонда E=-gradj (9.11).

5. Суперпозиция принципі. Диполь өрісі. Егер электростатикалық өрісте бірнеше нүктелік заряд берілсе, онда олардың бір нүктедегі қорытқы кернеулігі жеке зарядтардың сол нүктеде тудыратын кернеуліктерінің векторлық қосындысы болады және оны электр өрістерінің суперпозиция принципі деп атайды: E=E₁+E₂+E₃+…+E_n (9.12)

Суперпозиция принципі зарядтардың кез келген жүйесінің өріс кернеулігін есептеп табуға мүмкіндік береді.

Бір-бірінен l қашықтықта орналасқан әр аттас зарядталған екі нүктелік зарядтардың жиынтығы диполь деп аталады. Зарядтар арқылы жүргізілген түзу- диполь осі деп аталады. Диполь осі бойынша теріс зарядтан оң зарядқа қарай бағытталған және зарядтардың арақашықтығы l -ге тең вектор диполь иіні деп аталады (24-сурет). Оң заряд шамасының зарядтар ара қашықтығына көбейтіндісін және диполь иінінің бағытымен бағыттас векторды дипольдің электр моменті деп айтады: P = q l (9.13)

l. P

q^- q⁺

24-сурет.

Диполь өріс кернеулігі зарядтар шамасы арқылы емес, диполь моменті арқылы анықталады: E=kP/er³ (9.14)

Бір текті электр өрісінде орналасқан дипольдің әрбір зарядына күш әсер етеді. F₊=+ q E, F= q E. Бұл күштер бір-біріне қарама-қарсы бағытталады да күш моментін туғызады. Күш моменті дипольді бұруға тырысады. Сөйтіп, біртекті электр өрісі тарапынан дипольға бұрушы момент әсер етеді. Ол момент электр моментіне, дипольдің электр өрісіне орналасуына және электр өрісінің кернеулігіне тікелей байланысты. Біртекті электр өрісінде орналасқан диполь электр өрісінің күш сызықтарына параллель орналасуға тырысады. Дипольға әсер етіп тұрған екі күш шамасы жағынан тең, ал бағыты жағынан қарама-қарсы болғандықтан, күштер дипольді тек бұрады, орнынан жылжытпайды. Ал егер диполь әртекті электр өрісінде орналасқан болса, онда дипольге әсер ететін күштер шама жағынан әртүрлі болады, диполь бұрылып қана қоймайды, ол орнынан жылжиды.

6. Электр өрісінің кернеулік сызықтары. Кернеулік векторының ағыны. Электр өрісі графиктік түрде әрбір нүктесінде Е кернеулік векторымен сәйкес келетін жанама сызықтары- кернеулік сызықтарымен

а) 25-сурет б)

көрсетіледі. Кернеулік электр өрісінің күштік сипаттамасы болып санала-

ды. Кернеулік сызықтары-тұйықталмаған қисықтар. Ол оң зарядтардан басталып, теріс зарядтарға аяқталады. Өрістің күш сызықтары қиылыспайды (25, а-сурет). Барлық нүктелеріндегі кернеулігінің шамасы мен бағыты бірдей болатын өріс біртекті өріс деп аталады. Біртекті өрістің күш сызықтары бір-бірінен бірдей қашықтықта жататын параллель түзулер (25, б-сурет).

Кернеулік сызықтарының жиілігі Е -нің сан мәніне тең болсын. Сонда белгілі бір бетті тесіп өтетін кернеулік сызықтарының жалпы санын сол беттен өтетін кернеулік ағыны немесе өрістің кернеулік ағыны деп атайды. Мысалы, біртекті электр өрісінде S жазық бетті тесіп өтетін кернеулік векторлар ағынын анықтайық (26-сурет). Электр өрісінің күш сызықтары S бетін перпендикуляр бағытта тесіп өтсін, сонда кернеулік сызықтардың S бетке көбейтіндісі- кернеулік векторының ағыны деп аталады, оны Ф әрпімен белгілейді: Егер де S^¢ жазық бет өрістің кернеулік сызықтарына белгілі бір бұрышпен орналасса (26-сурет): Ф=EScosa.

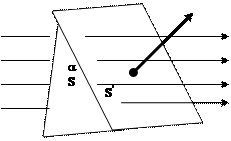n Кернеулік сызықтары

E біртекті емес кез келген

Тұйық бетті тесіп өтсе,

онда векторлық ағыны

(27-сурет):

Ф=ò_s E d S (9.15)

26-сурет

Әртүрлі ортаның шекарасында

және диэлектриктерде өтетін кернеу-

лік векторының өзгерістері электр

өрістерін есептеуде қиындықтар

туғызбас үшін электрлік ығысу век-

торы немесе электрлік индукция

векторы деген шама енгізіледі, ол

D әрпімен белгіленеді.

D= ee₀ E (9.16)

Электрлік ығысу векторының ағыны:

Ф=ò_sD_ndS (9.17)

27-cурет

7. Гаусс теоремасы. Электростатикалық өрісті есептеу әдістері. Гаусс теоремасын әр текті өріс кернеулігі үшін орыс математигі М.В.Остроградский қорытып шығарды. Заряд көлемдік тығыздығы r болатын тұйықталған беттің ішінде үздіксіз таралса, яғни r=dq/dV, онда V көлем ішінде зарядтың шамасы: Sq_i= òr dV. Бұдан Гаусс теоремасы Ф= (9.18) болып шығады. Енді Гаусс

теоремасын вакуумдағы кейбір электро-

+s -s статикалық өрістер үшін жазайық.

1.Біркелкі зарядталған шексіз жазықтық

өрісі үшін E=s/2 e₀ (9.19).

2. Әртекті зарядталған екі шексіз парал-

лель жазықтықтар өрісі үшін (28-сурет):

E=0 E=s/ e₀ E=0 E=s/ e₀ (9.20)- жазықтықтар аралығындағы

қорытқы кернеулік, ал жазықтық сыртында

28-сурет кернеулік нольге тең.

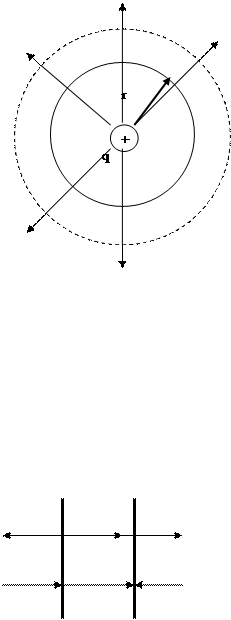
3. Біркелкі зарядталған сфералық бет үшін: Сфералық беттің радиусы- R, заряды- q, беттік тығыздығы- s деп алсақ, E=kq/r² (9.21), ал сфераның ішкі бетінде E=0. 4. Көлемі бойынша зарядталған шар үшін: шардың сыртында кернеулік үшін (9.21) формула қолданылады, ал шардың ішінде E=kqr^¢/R³ (9.22), мұнда r^¢- ішкі сфераның радиусы. 5. Біркелкі зарядталған шексіз цилиндрдің (жіп) өрісі. E=t/2pe₀r (9.23)-цилиндрдің сыртқы беті үшін кернеуліктің мәні, мұнда t –зарядтың сызықтық тығыздығы, цилиндрдің ішінде кернеулік нольге тең болады.

8. Идеал өткізгіштер. Зарядтардың беттік тығыздығы. Электростатикалық қорғаныс. Егер электростатикалық өріске бір өткізгішті ендірсек немесе өткізгішке аздаған заряд берсек, онда электрлік күштердің әсерінен осы зарядтар орын ауыстыра бастайды. Сөйтіп зарядтар тепе-тең болып бөлінгенге дейін, өткізгіштер қозғалыста болады. Осы кезде өткізгіштің барлық жеріндегі өріс кернеулігі нольге тең болады, себебі, өткізгіш ішіндегі потенциалдар тұрақты болу керек. Сонымен қатар өткізгіш бетінің әрбір нүктесіндегі өріс кернеулігі бетке нормаль бойымен бағытталады (25-суретті қараңыз). Демек, тепе-теңдік жағдайда өткізгіштің беті эквипотенциал болады. Тепе-теңдік кезінде өткізгіш ішіндегі кез келген нүктеде өріс болмағандықтан, бет арқылы электрлік зарядтардың ығысу векторының ағыны нольге тең болады. Ол зарядтардың қосындысы да Остроградский-Гаусс теоремасына сәйкес нольге тең. Олай болса, тепе-теңдік кезінде өткізгіштің ішіндегі ешбір жерде артық заряд болуы мүмкін емес, сөйтіп зарядтар өткізгіштің бетінде белгілі бір тығыздықпен (s) орналасуы керек. Өткізгіштің бірлік ауданына сәйкес келетін заряд шамасы зарядтың беттік тығыздығы деп аталады, s=dq/dS (9.24)

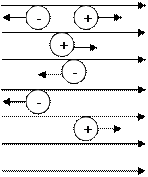
Егерсыртқы электростатикалық өріске нейтрал өткізгішті орналастырсақ, онда еркін зарядтар (электрондар, иондар) орын ауыстыра бастайды: оң зарядтар өріс бойынша, ал теріс зарядтар өріске қарсы (29,а-сурет). Өткізгіштің бір жақ ұшында оң зарядтардың артығы, келесі ұшында теріс зарядтың артығы жинала бастайды. Бұл зарядтар индукцияланған деп аталады. Бұл процесс өткізгіш ішіндегі өріс кернеулігі нольге теңелгенше жалғаса береді, өткізгіш сыртындағы сызықтар оның бетіне перпендикуляр болады (29,б-сурет).

-

- +

- E=0 +

- +

- +

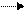а) 29-сурет б)

Соныменен, электростатикалық өріске енгізілген нейтрал өткізгіш кернеулік сызықтарының бір бөлігін айырады; олар теріс индукцияланған зарядтарға аяқталады да оң зарядтарда қайтадан басталады. Сыртқы электростатикалық өрісте орналасқан өткізгіштегі беттік зарядтардың қайта бөліну құбылысы электростатикалық индукция деп аталады.

Тепе-теңдік жағдайда өткізгіш ішінде заряд болмайды, сонда оның ішкі қуысындағы зарядтардың орналасу конфигурациясына әсер етпейді. Сондықтан да қуыс ішінде де өріс болмайды. Егер осы өткізгішті қуысымен жермен қоссақ, онда қуыстың барлық нүктесінде потенциал нольге тең болады, яғни қуыс толығымен сыртқы электростатикалық өрістен оқшауланған болады. Осыған электростатикалық қорғаныс негізделген. Электростатикалық қорғаныс дегеніміз-денелерді экрандау, мысалы, өлшеу құралдарын сыртқы электростатикалық өрістердің әсерінен экрандау.

9. Электр сыйымдылық. Конденсаторлар. Конденсатор энергиясы. Басқаөткізгіштерден, денелерден және зарядтан оқшау орналасқан өткізгіш үшін келесі өрнекті жазуға болады: q=Cj, осындағы C=q/j (9.25) шамасын оқшауланған өткізгіштің электр сыйымдылығы деп атайды. Электр сыйымдылық сан жағынан өткізгіштің потенциалын бір өлшемге арттыруға қажетті зарядқа тең. Өткізгіштің сыйымдылығы оның пішіні мен өлшеміне тәуелді де, бірақ өткізгіштің тегіне, агрегаттық күйіне және оның ішкі қыртыстарының өлшемдеріне тәуелсіз. Өлшем бірлігі- фарада болады. (9.6) сәйкес, диэлектр өтімділігі e болатын біртекті ортада орналасқан радиусы R оқшауланған шардың потенциалы j=kq/ e R. (9.26) формуланы пайдаланып, шардың сыйымдылығын аламыз C=4pe₀eR (9.27)

Өткізгіш сыйымдылығы үлкен болу үшін оның өлшемдері де үлкен болуы керек. Практикада өлшемдері кіші, бірақ көп заряд жинақтай алатын сыйымдылығы үлкен құрылғылар қажет болады. Ондай құрылғыларды конденсаторлар деп атайды. Конденсатор диэлектрикпен бөлінген екі өткізгіштен (астардан) тұрады. Астарларының пішініне қарай конденсаторлар жазық, цилиндрлік және сфералық болып бөлінеді.

Конденсаторларды параллель қосқанда

1 +j (30,а-сурет) олардың астарларындағы

потенциалдары j₁, j₂, j₃ де, сыйым-

дылықтары С₁, С₂,С_3, зарядтары q₁,

+ + + + + + q₂, q₃ болады. Конденсатор батарея-

С₁ С₂ С₃ ларындағы заряд: q=S q_i, барлық

- - - - - - батареялардың толық сыйымдылы-

ғы: C=S C_i (9.32)

+ С₁ С₂ С₃ -

2 -j

Dj₁ Dj₂ Dj₃

а 30-сурет б

Конденсатор сыйымдылығы деп конденсаторда жинақталған заряд шамасының оның астарларындағы потенциалдар айырмасына қатынасын айтады: C=q/(j₁-j₂) (9.28). Сонда жазық конденсатордың сыйымдылығын жазатын болсақ, C=eeS/d (9.29), мұндағы S -пластиналардың ауданы, d -олардың ара қашықтығы. Цилиндр тәрізді конденсатор электр сыйымдылығы: C=(2pee₀l)/ln(r₂/r₁) (9.30). Сфералық конденсатордың электр сыйымдылығы: C=(4pee₀r₁ r₂)/(r₂-r₁) (9.31).

Конденсаторларды тізбектеп қосқанда (30,б-сурет) олардың астарларын-дағы зарядтардың шамалары бірдей, ал потенциалдар айырымы мен

сыйымдылықтары әртүрлі болады. Барлық батарея үшін потенциалдар айырымы Dj=qS(1/C_i), толық сыйымдылық: 1/С=S1/C_i (9.32)

Кез келген өткізгіштер сияқты, зарядталған конденсаторлардың да энергиялары болады, ол энергия шамасы: W=q²/(2C)=C Dj²/2.

Электростатикалық өріс энергиясы: W=e₀eE²V/2 (9.33)

Энергияның көлемдік тығыздығы: w=e₀eE²/2=ED/2 (9.34)

Бақылау сұрақтар

§ Зарядтың сақталу заңын түсіндіріңіз. Мысал келтіріңіз.

§ Кулон заңы қалай оқылады? Мағынасын түсіндіріп, формуласын жазыңыз.

§ Электростатикалық өріс деген не? Өрісті сипаттаушы шамаларды түсіндіріңіз.

§ Сызықтық, беттік және көлемдік тығыздық деген не?

§ Гаусс теоремасы. Оның өрісті есептеуге қолданылуы.

§ Конденсаторлар, түрлері, электр сыйымдылық, өріс энергиясы.

Дата добавления: 2014-01-04