Ітераційні методи

3.1 Метод простої ітерації

Нехай система лінійних рівнянь

(4)

Якимось чином зведеться до вигляду

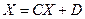, (5)

де С – деяка матриця, а D – вектор стовпчик.

Виходячи з довільного вектора , будуємо ітераційний процес , (6) де

або в розгорнутій формі:

(7)

Обчислюючи ітерації отримаємо послідовність векторів

Доведено, якщо елементи матриці С задовольняють одній з умов:

(8)

або , (9)

то процес збігається до точного розв’язку системи Х при будь-якому початковому векторі , тобто

Таким чином, точний розв’язок отримується лише як результат нескінченного процесу й будь-який вектор 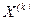з отриманої послідовності є наближеним розв’язком. Оцінка похибки цього наближеного розв’язку 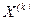дається однією з наступних формул:

у разі виконання умови (6), (8*)

або, якщо виконана умова (7). (9*)

Процес ітерації закінчується тоді, коли указані оцінки свідчать про досягнення заданої точності.

Початковий вектор вибирається загалом довільно. Іноді беруть =D, але найбільш доцільно у якості вектора брати значення отримані грубого прикидкою.

Приведення системи (4) до виду (5) можна здійснювати у різні способи. Важливо лише пам’ятати про необхідність виконання умови (8) або (9).

Наведемо один з способів приведення до виду (5)

Якщо діагональні елементи , то систему (1) записують у вигляді:

(10)

В цьому випадку елементи матриці визначають за формулами:

, тоді умови (8) та (9) приймають вид:

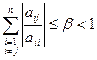(8”) (9”)

Останні нерівності будуть виконані, якщо діагональні елементи задовольняють умові:, тобто модулі діагональних коефіцієнтів для кожного рівняння системи більші суми модулів всіх інших коефіцієнтів (без вільних членів).

Якщо метод ітерацій збігається, то він дає наступні переваги порівняно з іншими методами:

1) якщо ітерації збігаються швидко, то перевага в часі.

2) похибки округлення значно менші ніж в методі Гаусса. Ця обставина часто використовується для уточнення даних, отриманих методом Гаусса.

3) метод ітерацій зручно застосовувати для СЛАР у яких значна кількість коефіцієнтів = 0

4) виконуються однотипні дії зручно програмувати

Дата добавления: 2014-01-04