Колебания цепочки атомов 2-х сортов

Предположим, что имеем цепочку легких атомов с массой m и тяжелых с массой M (см. рисунок 7.5). Расстояние между атомами - a.

Пусть легкие атомы занимают четные положения, а тяжелые - нечетные. Запишем законы движения для легких и тяжелых частиц. Обозначим u_2n - смещение атома с массой m, u_2n-1 - смещение атома с массой M. Учтем влияние лишь ближайших соседей на движение данного атома. Влиянием более удаленных частиц будем пренебрегать.

Тогда для легких частиц:

,

а для тяжелых частиц:

.

С учетом того, что колебания атомов разных масс могут происходить с различными амплитудами u₁ и u_2, решение этой системы уравнений будем искать в следующем виде:

,

.

Подставим эти решения в уравнения движения и, сократив общий множитель 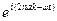в каждом из уравнений, получим систему уравнений относительно u₁ и u₂:

(2b-mw²) u₁ -2 b cos (ka) u₂=0

-2 b cos (ka) u₁ + (2b-Mw²) u₂=0

Система линейных однородных уравнений будет иметь ненулевое решение в том случае, если определитель равен нулю.

Отсюда получаем уравнение, связывающее частоту w и волновое число k:

Корни этого уравнения

.

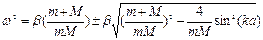Отрицательные значения w не имеют физического смысла. Поэтому каждому волновому числу k соответствуют два значения w, а, следовательно, и две моды колебаний.

Итак, решение задачи о колебаниях атомов двух сортов в цепочке, приводит к двум кривым зависимости w(k), которые получили название двух ветвей закона дисперсии (см. рисунок 7.6). Нижнюю кривую называют акустической ветвью, верхнюю - оптической ветвью. Во всем интервале изменений волновых чисел k частота оптических колебаний больше частоты акустических.

Нижняя ветвь ведет себя аналогично кривой для одноатомной цепочки, поэтому она получила название акустической. Верхняя ветвь достигает максимальных значений при k=0 и принимает минимальные значения при . Эту ветвь называют оптической, так как длинноволновые оптические моды в ионных кристаллах могут взаимодействовать с электромагнитным излучением.

Как видно из рисунка 7.6, две ветви разделены полосой запрещенных частот (заштрихованная область на рисунке), в которой уравнения движения не имеют решения. Однако если в цепочке заменить, например, один или несколько атомов массы M на атомы массы m, т.е. ввести в структуру дефекты, то в запрещенной области частот появятся решения, которые называют локальными модами.

Выясним физический смысл различия между акустическими и оптическими модами колебаний атомов в цепочке.

Если рассмотреть нижнюю ветвь колебаний, то для нее амплитуды колебаний легких и тяжелых частиц будут равны (см. рисунок 7.7). Отсюда следует, что для нижней ветви спектра, колебания, смещается синхронно с одинаковыми амплитудами. Фактически для нижней ветви спектр колебаний будет представлять синусоиду, в которой смещаются вверх - вниз синхронно легкие и тяжелые атомы и соответственно их центры масс.

Рассмотрим верхнюю ветвь колебаний. Для колебания легких и тяжелых частиц происходят в противофазе, причем центр масс не меняет своего положения (см. рисунок 7.8).

Таким образом, в цепочке, состоящей их атомов двух сортов атомов, происходит разделение колебаний на акустическую и оптическую ветви. При этом частота оптических колебаний слабо зависит от волнового числа к, а для акустической ветви эта зависимость более сильная. Естественно предположить, что с усложнением модели и ее обобщением на 3-х мерный случай, спектр колебания также будет представлять набор ветвей колебаний (часть акустических, часть оптических). Спектр колебания реальных материалов также может быть представлен в виде ветвей колебаний, что соответствует экспериментальным данным.

Дата добавления: 2014-01-04