
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение идеального газа. Экспериментальные газовые законы
|
|
|
|
ИДЕАЛЬНЫЕ И РЕАЛЬНЫЕ ГАЗЫ.
Лекция 10
Дополнительная
Основная
1. Грабовский Р.И. Курс физики / Р. И. Грабовский.– СПб.; Издательство «Лань», 2002.-608 с.
2. Пронин В.П. Краткий курс физики / В.П. Пронин. –Саратов: ФГОУ ВПО «Саратовский ГАУ», 2007 г. – 200 с.
3. Трофимова Т.И. Курс физики / Т.И. Трофимова. – М.: «Высшая школа». 2003 г. – 350с.
1 .Матвеев А.Н. Механика и теория относительности. Учебное пособие/ С.-Петербург: Издательство «Лань», 2009г. 500экз.
2 .Рогачев Н.М. Курс физики. Учебное пособие// С.-Петербург: Издательство «Лань», 2010г.- 448с. 1000 экз.
3 .Трофимова Т.И. Физика в таблицах.. М.: «Высшая школа». 2008г
При изучении кинетической теории газа рассматривают так называемый идеальный газ. Газ, в котором пренебрегаем силами межмолекулярного взаимодействия и объемом молекул газа. Процессы в газе, при которых меняются его параметры состояния, называются газовыми процессами. Газовые процессы, в которых один из параметров остается неизменным называются изопроцессами («изо» - равный).
Для идеальных газов справедливы следующие законы:
1. Закон Бойля-Мариотта. (Бойль – англ., 1662г.; Мариотт – франц., 1667г.)
Если Т = const данной массы газа (m = const), а давление P и V – объем изменяются. Процесс называется изотермическим.
«Для данной массы газа при постоянной температуре давление газа изменяется обратно пропорционально объему». PV = const (1)
Для двух состояний газа закон имеет вид: P V
V = P
= P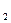 V
V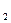 , где P
, где P и V
и V - начальное состояние, P
- начальное состояние, P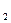 и V
и V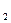 - в конечном состоянии. Графически изотермический процесс представляется в виде гиперболы, называемой изотермой (рис. 28).
- в конечном состоянии. Графически изотермический процесс представляется в виде гиперболы, называемой изотермой (рис. 28).
 |
Р
Т = const
V, м
Рисунок 28
V
 Р = const
Р = const
 |
t, 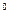 С
С
 |
 Рисунок 29
Рисунок 29
2. Законы Гей-Люссака. (1802 г.)
Давление Р = const и m = const. Процесс изобарический(Рис.29).
«Для данной массы газа при постоянном давлении объем газа изменяется линейно с температурой».
V = V
= V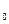 (1 + dt) (2),
(1 + dt) (2),
где V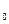 - объем при t = 0
- объем при t = 0 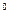 С;
С;
V - объем газа при t;
- объем газа при t;
d – коэффициент объемного расширения; d = 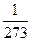 град
град .
.
Графически изобарический процесс представляет прямую. 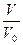 =
= 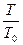 (3)
(3)
«При постоянном давлении объем газа пропорционален абсолютной температуре».
Объем V = const и m = const. Процесс изохорический. Иногда этот закон называют закон Шарля.
«Для данной массы газа при постоянном объеме давление газа изменяется линейно с температурой».
P = P
= P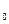 (1 + γt) (4),
(1 + γt) (4),
где P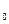 - давление при t = 0
- давление при t = 0 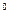 С;
С;
γ – термический коэффициент давления; γ = 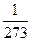 град
град .
.
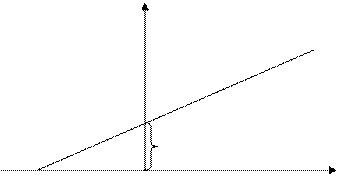
Графически изохорический процесс представляет прямую (рис. 30).
 |
P
V = const
P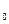
- 273 0 t, 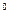 С
С
Рисунок 30
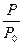 =
= 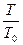 (5)
(5)
«При постоянном объеме давление газа пропорционально абсолютной температуре».
3. Закон Дальтона (1801 г., англ.)
Парциальным давлением газа, входящего в газовую смесь, называется давление, которое имел бы этот газ, если бы он один занимал весь объем, представленной смеси.
«Давление газовой смеси равно сумме парциальных давлений входящих в нее газов».
P = P + P
+ P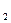 + P
+ P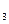 + P
+ P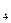 + … + P
+ … + P (6)
(6)
4. Закон Авогадро (итал., 1811 г.)
«При одинаковых температуре и давлении моли любых газов занимают одинаковые объемы».
При нормальных условиях (температура 273,16 К и давлении 1,0133 Па) этот объем равен 22,41  .
.
4. Уравнение Клапейрона-Менделеева.
Это уравнение выражает объединенный закон газового состояния. Он устанавливает связь между P,V и T при их изменении. Состояние некоторой массы m газа характеризуется параметрами P ,V
,V и T
и T . Переведем ее в другое состояние P
. Переведем ее в другое состояние P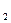 ,V
,V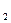 и T
и T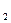 в два этапа: а) изотермически (T = const) по закону Бойля – Мариотта V
в два этапа: а) изотермически (T = const) по закону Бойля – Мариотта V P
P = V
= V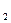 P
P , откуда P
, откуда P =
= 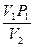 ; б) изохорически (V
; б) изохорически (V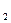 = const). Этап описывается законом Гей-Люссака (5):
= const). Этап описывается законом Гей-Люссака (5):
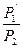 =
= 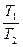 подставим значение P
подставим значение P , получим
, получим  =
= 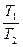 , откуда
, откуда  =
= 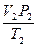 .
.
Для данной массы газа величина 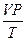 остается неизменной:
остается неизменной:
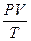 = B = const (7) – уравнение Клайперона (1834г.)
= B = const (7) – уравнение Клайперона (1834г.)
Но В является различной для различных газов. Она зависит от массы газа и его природы. Менделеев (1875г.) объединил уравнение (7) с законом Авогадро и получил
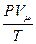 = R (8),
= R (8),
где R – универсальная газовая постоянная (R = 8,32  ).
).
Иногда PV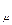 = RT (9) – уравнение Клапейрона-Менделеева для одного моля газа.
= RT (9) – уравнение Клапейрона-Менделеева для одного моля газа.
PV =  RT (10) – уравнение состояния идеального газа для любой массы газа.
RT (10) – уравнение состояния идеального газа для любой массы газа.
Молекулы, благодаря хаотического движения, ударяют о стенки сосуда с некоторой небольшой силой, перпендикулярной к поверхности стенки. Так как молекул бесчисленное множество стенки сосуда испытывают сравнительно большую силу. Эта сила, рассчитанная на единицу площади – есть давление газа, которое обусловлено тепловым давлением молекул.
Давление (Р) газа является функцией φ средней кинетической энергии поступательного движения его молекул 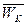 :
:
Р = φ (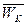 )
)
Введем следующие упрощения:
1. Молекулы - упругие шарики пренебрежительно малого размера (мат. точки).
2. Силы сцепления между молекулами пренебрежительно малы.
3. Силы отталкивания между молекулами проявляются только в моменты взаимодействия.
4. Число взаимостолкновений между молекулами пренебрежимо мало по сравнению с числом их ударов о стенки сосуда.
Таким образом, газ является идеальным.
Р =  n
n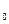
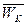 (12) - уравнение Клаузиуса.
(12) - уравнение Клаузиуса.
«Давление газа прямо пропорционально средней кинетической энергии поступательного движения молекул, содержащихся в единице объема газа».
Средняя кинетическая энергия поступательного движения молекул идеального газа равна:
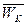 =
=  , так как скорость молекул зависит от температуры газа, то и средняя энергия зависит от температуры.
, так как скорость молекул зависит от температуры газа, то и средняя энергия зависит от температуры.
Обе части уравнения Р =  n
n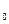
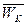 умножим на молярный объем газа V
умножим на молярный объем газа V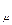 . Р V
. Р V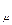 =
=  n
n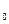
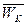 V
V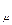 . Зная, что n
. Зная, что n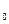 V
V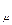 = N
= N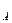 (постоянная Авогадро), тогда
(постоянная Авогадро), тогда
Р V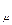 =
=  N
N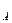
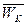 . Согласно уравнению Клапейрона-Менделеева Р V
. Согласно уравнению Клапейрона-Менделеева Р V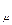 = RT. Приравниваем последние выражения, откуда имеем:
= RT. Приравниваем последние выражения, откуда имеем:  N
N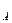
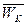 = RT откуда
= RT откуда 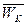 =
= 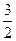
 . Обозначив
. Обозначив 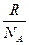 = k, получим
= k, получим 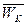 =
= 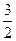 k T (13), где k – постоянная Больцмана.
k T (13), где k – постоянная Больцмана.
«Средняя кинетическая энергия поступательного движения молекул идеального газа пропорциональна абсолютной температуре и зависит только от нее».
k = 1,38 * 10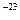

Подставим в Р =  n
n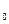
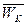 вместо
вместо 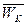 ее выражение (13), получим зависимость давления газа от температуры: Р =
ее выражение (13), получим зависимость давления газа от температуры: Р =  n
n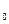
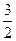 k T = n
k T = n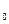 k T (14)
k T (14)
Из формулы (14) получаем:  N
N =
= 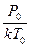 (15)
(15)
«При одинаковых температурах и давлении все газы содержат в единице объема одинаковое число молекул».
Число молекул N в 1 м
в 1 м при нормальных условиях, называется числом Лошмидта.
при нормальных условиях, называется числом Лошмидта.  N
N = 2,69 * 10
= 2,69 * 10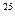 м
м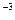 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 984; Нарушение авторских прав?; Мы поможем в написании вашей работы!