Внутреннее трение (вязкость)

Выделим два параллельных слоя газа (жидкости), движущихся с различными скоростями. В процессе хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

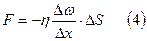- уравнение внутреннего трения или закон Ньютона.

Сила внутреннего трения, возникающая в плоскости соприкосновения двух скользящих относительно друг друга слоев газа, пропорциональна площади их соприкосновения ΔS и градиенту скорости Δω/Δx. Знак минус показывает, что импульс переносится в направлении убывания скорости.

Обозначив 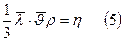Коэффициент пропорциональности η,зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью).

η – коэффициент пропорциональности внутреннего трения (коэффициент вязкости)

Если положить, что ΔS=1м² и Δω/Δx=-1сек^-1, тогда F=η.

Коэффициент вязкости численно равен силе внутреннего трения, действующей на 1 м² площади соприкосновения параллельно движущихся слоев газа при градиенте скорости в -1сек^-1.

η измеряется в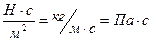

Из формулы (5) видно, что η не зависит от давления, за исключением случая сильного разрежения газа, т.е. когда λ – средняя длина свободного пробега молекул становится больше размера сосуда, в котором находится газ.

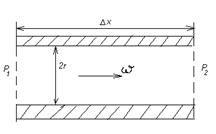
Для жидкостей сила внутреннего трения выражается законом Ньютона. η – коэффициент вязкости для жидкостей находится в пределах 10^-3-1 кг/м∙с. И в зависимости от температуры (η уменьшается с повышением температуры). Вязкость уменьшает скорость течения жидкости по трубе (руслу). Пуазейль (1841г.) установил, что «Средняя скорость ω ламинарного течения жидкости по трубе пропорциональна градиенту давления Δρ/Δx жидкости, квадрату радиуса r трубы и обратно пропорциональна коэффициенту вязкости η жидкости.

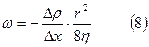, где Δρ=Ρ1-Ρ2 - закон Пуазейля при ламинарном течении (см.рис.31)

Объем жидкости ΔV, протекающий за Δt равен:

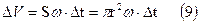, где S=πr² – площадь поперечного сечения трубы. Подставив значение скорости из формулы (8) и (9), получим

Рисунок 31 - формула Пуазейля.

Объем жидкости, протекающей по трубе, пропорционален четвертой степени радиуса трубы, времени и градиенту давления жидкости и обратно пропорционален коэффициенту вязкости жидкости.

Тело, движущееся в жидкости, испытывает сопротивление (трение) со стороны жидкости. Сила сопротивления зависит от скорости движения тела, его размеров и формы. Стокс установил:Для тел шарообразной формы, движущихся с небольшой скоростью, сила сопротивления жидкости F пропорциональна коэффициенту вязкости η, радиусу шара r и скорости движения ω.

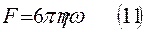- закон Стокса

Закон применим также к движению шарообразных тел в газе.

Шар массой m и радиусом r падает со скоростью ω в жидкости с вязкостью η (рис.32). На шар действуют три силы: F₁-сила тяжести, F₂-выталкивающая сила, F-сила сопротивления жидкости. F₁ и F₂ – постоянны, а F – возрастает с увеличением скорости движения шара. С некоторого момента времени силы уравновесят друг друга F₁= F₂+F

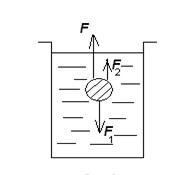
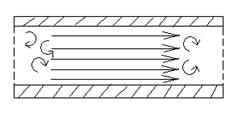
Рисунок 32 Рисунок 33

Шар движется равномерно. Согласно закону Ньютона

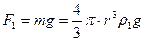, а по закону Архимеда , где ρ₁ и ρ₂ – плотность шара и жидкости.

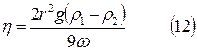
Из (12) найдем скорость падения шара: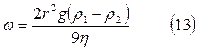

Ламинарный характер течения жидкости (газа) имеет место при небольших скоростях. Когда скорости слоев перемешиваются, такое течение называется турбулентным. Скорость течения по сечению трубы становится почти одинаковой и лишь вблизи ее стенок возникают очень большие градиенты скорости (рис.33)

Турбулентное течение наблюдается на узких и мелких местах рек, здесь образуются водяные вихри – водовороты. Характер течения зависит от безразмерной величины, называемой числом Рейнольдса:

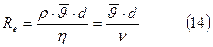, где 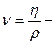кинематическая вязкость, ρ- плотность жидкости или газа, η- коэффициент вязкости жидкости, d- характерный для поперечного сечения размер, например, радиус или диаметр при круглом сечении, квадратное сечение и т.д.

При малых значениях числа (R≤1000) наблюдается ламинарное течение. Переход от ламинарного течения к турбулентному происходит в интервале 1000≤R≤2000. Для воды, текущей в гладкой, цилиндрической трубе, R=2300, течение - турбулентное.

Вопросы для самоконтроля

1.В чем сущность явления переноса? Каковы они и при каких условиях возникают?

2.Объясните физическую сущность законов Фурье, Фика, Ньютона.

3.Переносом какой физической характеристики молекулами газа обусловлено явление теплопроводности?

4.Чем обусловлен ламинарный хар-р движения газа вблизи поверхности твердого тела?

5.Какую единицу имеет коэффициент диффузии? Коэффициент теплопроводности? Коэффициент вязкости?

6.Соотношения между коэффициентами диффузии, теплопроводности и вязкости?

7.Объяснить ламинарное и турбулентное течение жидкости.

8.Напишите закон Пуазейля, формулу Пуазейля для объема жидкости.

9.Метод Стокса для определения коэффициента вязкости жидкости.

СПИСОК ЛИТЕРАТУРЫ

Дата добавления: 2014-01-04