Поток вектора напряженности

Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью 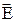пронизывают некоторую площадку S, то поток вектора напряженности (число силовых линий через площадку) будет определяться формулой

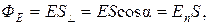
где E_n – произведение вектора 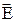на нормаль 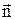к данной площадке (рисунок 2.5).

Рисунок 2.5

Полное число силовых линий, проходящих через поверхность S, называется потоком вектора напряженности Ф_Е через эту поверхность.

Элементарный поток вектора напряженности через площадку dS (рис. 5) определится соотношением:

,

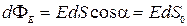где 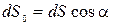– проекция 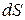на направление нормали .

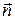В векторной форме можно записать 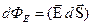– скалярное произведение двух векторов, где вектор .

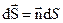Таким образом, поток вектора 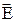есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.

Полный поток вектора напряженности через любую площадку S можно определить тогда 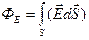, а поток через замкнутую поверхность, окружающую заряд или заряженное тело равен .

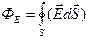Так как напряженность поля, созданного в любой точке пространства зависит от величины заряда, создающего это поле, то поток вектора напряженности электростатического поля через любую площадку, находящуюся в этом поле также зависит от величины заряда.

Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.

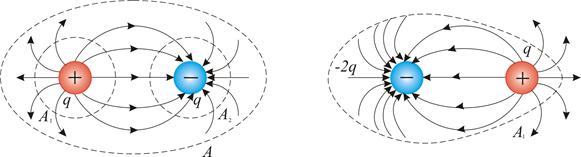
Рисунок 2.6 Рисунок 2.7

Для рисунка 2.6 – поверхность А ₁ окружает положительный заряд и поток здесь направлен наружу, т.е. 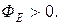Поверхность А ₂ – окружает отрицательный заряд, здесь 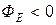и направлен внутрь. Общий поток через поверхность А равен нулю.

Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность А отрицательный.

Таким образом, поток вектора напряженности зависит от заряда.

2.3. Теорема Остроградского – Гаусса (теорема Гаусса)

К.Ф. Гаусс (1777–1855) выдающийся немецкий математик, астроном и физик в 1839г. предложил теорему, которая устанавливает связь потока вектора напряженности электрического поля череззамкнутую поверхность со значением заряда q, находящегося внутри этой поверхности. Эта теорема выведена математически для векторного поля любой природы русским математиком М.В. Остроградским (1801-1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.

Теорема Остроградского – Гаусса (теорема Гаусса): поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :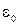

.

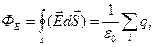Докажем эту теорему. Пусть поле создается точечным зарядом q. Окружим заряд замкнутой поверхностью S произвольной формы. Разобьем замкнутую поверхность на элементарные площадки dS, к каждой из которых проведем вектор нормали .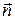

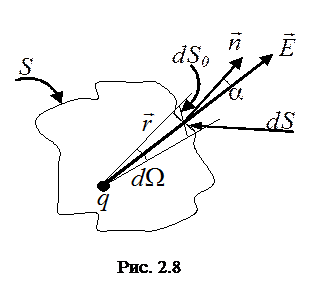Элементарный поток вектора напряженности через площадку dS (рис. 2.8) определится соотношением:

,

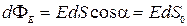где 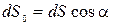–проекция 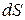на направление нормали 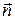. Тогда 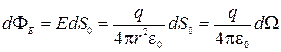, где 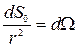- элементарный телесный угол, под которым элемент 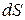виден из места положения заряда. Вычислим поток вектора напряженности через замкнутую поверхность S от точечного заряда q, находящегося внутри этой поверхности.

,

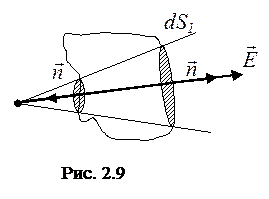
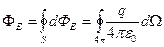так как 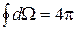, то

.

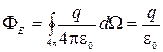Как видно, поток вектора напряженности выходящий из поверхности не зависит от формы поверхности, охватывающей заряд и пропорционален величине заряда.

Если заряд находится вне замкнутой поверхности, то суммарный поток через любые элементарные площадки dS₁ и dS₂, находящиеся внутри телесного угла d Ω (рис. 2.9) равен сумме потоков напряженности выходящего из этой поверхности (положительный поток) и входящего в нее (отрицательный поток).

Тогда 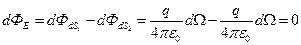, следовательно, поток напряженности электрического поля через любую поверхность S, не охватывающую заряды равен нулю, т.е. Ф_Е =0.

Пусть внутри замкнутой поверхности имеется зарядов, тогда алгебраическим суммированием (согласно принципу суперпозиции) находим, что общий поток вектора напряженности через замкнутую поверхность равен .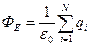

Теорема доказана.

Таким образом теорему Гаусса можно сформулировать следующим образом: поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на :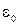

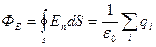(1),

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью 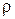, то теорема Гаусса имеет вид:

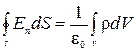(2)

где интеграл справа берется по объему V, охватываемому поверхностью S.

Необходимо обратить внимание на следующее обстоятельство: в то время как само поле 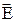зависит от конфигурации всех зарядов, поток 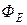сквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхности S. Это значит, что если передвинуть заряды внутри замкнутой поверхности, то 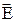изменится всюду, и на поверхности S, а поток вектора 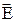через эту поверхность останется прежним.

Таким образом, чтобы рассчитать поле, созданное какой-то конфигурацией зарядов в данной точке, нужно через эту точку провести замкнутую поверхность произвольной формы и рассчитать поток вектора напряженности через эту поверхность. Так как по теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 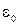, то, зная величину заряда, находящегося внутри замкнутой поверхности можно найти напряженность поля в интересующей нас точке пространства.

Рассмотрим примеры применения теоремы Гаусса.

Дата добавления: 2014-01-04