Дифференциальная форма теоремы Остроградского-Гаусса

С помощью дифференциальной формы теоремы можно рассчитать электростатическое поле при произвольном пространственном распределении зарядов. В ней установлена связь между объемной плотностью заряда ρ и изменением 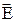в окрестности данной точки пространства.

Воспользуемся теоремой Остроградского-Гаусса, согласно которой поток вектора 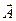через любую замкнутую поверхность равен интегралу от его дивергенции по объему, охватываемому этой поверхностью, т.е. 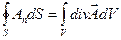. Дивергенцией вектора 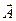(обозначается div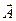) в какой либо точке поля называется, предел отношения потока вектора 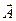через замкнутую поверхность S, охватывающую точку M, к объему ΔV части поля, ограниченной поверхностью S, при неограниченном уменьшении ΔV: .

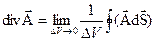Пусть заряд распределен в пространстве D V, с объемной плотностью 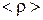. Тогда по теореме Остроградского – Гаусса

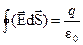; или ; .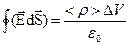

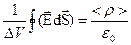Теперь устремим 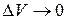, стягивая его к интересующей нас точке. Очевидно, что при этом 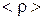будет стремиться к ρ в данной точке, т.е.

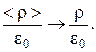
Величину, являющуюся пределом отношения 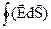к D V, при 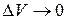, называют дивергенцией вектора 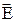и обозначается 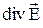. Тогда, по определению

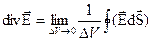. (11)

Аналогично определяется дивергенция любого другого векторного поля. Из этого определения следует, что дивергенция является скалярной функцией координат. В декартовой системе координат

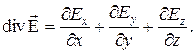(12)

Итак,

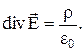(13)

Это теорема Остроградского-Гаусса в дифференциальной форме.

Это уравнение свидетельствует о том, что источником электростатического поля являются свободные электрические заряды.

Написание многих формул упрощается, если ввести векторный дифференциальный оператор 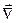(Набла)

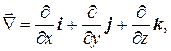(14)

где i, j, k – орты осей (единичные векторы).

Сам по себе оператор 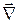смысла не имеет. Он приобретает смысл в сочетании с векторной или скалярной функцией, на которую символично умножается:

,

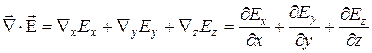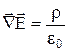. (15)

Формула (2.4.5) это тоже дифференциальная форма теоремы Остроградского-Гаусса.

В тех точках поля, где 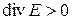– (положительные заряды) источники поля, где 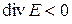– стоки (отрицательные заряды). Линии 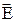выходят из источников и заканчиваются в стоках.

Контрольные вопросы

1. В чем заключается смысл теоремы Остроградского –Гаусса? Докажите теорему.

2. Как можно при помощи теоремы Остроградского –Гаусса рассчитать напряженность поля плоскости?

3. Как можно при помощи теоремы Остроградского –Гаусса рассчитать напряженность поля цилиндра или нити?

4. Как можно при помощи теоремы Остроградского –Гаусса рассчитать напряженность поля шара или сферы?

5. Как записать теорему Остроградского –Гаусса в дифференциальной форме?

6. Каков смысл дивергенции вектора?

Дата добавления: 2014-01-04