Состояния гетерогенных систем

ОСНОВЫ УЧЕНИЯ О ФАЗОВЫХ РАВНОВЕСИЯХ И ДИАГРАММАХ.

5.1. Основные понятия и определения. Понятие о равновесном состоянии.

С и с т е м а – вещество или смесь веществ, отделенные от окружающей среды таким образом, что в ней можно наблюдать изменения и конечное состояние в зависимости от определяющих условий.

Ф а з а – часть системы, обладающая по всему своему объему одинаковыми химическими, физическими, термодинамическими свойствами и имеющая поверхность раздела с другими фазами системы.

Различают чистые фазы, которые представлены, например, химическими соединениями определенного состава и смешанные фазы (газы, расплавы, твердые растворы, растворы), состав которых при изменении внешних условий может меняться.

Процессы, происходящие на границе раздела фаз, играют существенную роль в формировании структуры строительных материалов, исходным сырьем для которых являются различные дисперсные системы с развитой поверхностью.

Существуют системы однородные (гомогенные) – однофазные (это в основном газы и жидкости). В чистом виде в производстве строительных материалов эти системы используются крайне редко. Неоднородные системы состроят из 2-х и более фаз. При минимальном количестве фаз в системе одна из них является сплошной и называется дисперсионной средой (то, в чем ²растворено²), а другая – дисперсной фазой (то, что ²растворено²). Классификация дисперсных систем по агрегатному состоянию вещества фаз приведена ниже.

Таблица 3 – классификация дисперсных систем

Дисперсионная среда	Дисперсная фаза	Условное обозначение	Название системы и примеры
Твердая	Твердая	Т/Т	Твердые гетерогенные системы: минералы, сплавы, бетон, композиты
Жидкая	Ж/Т	Капиллярные системы: насыщенные пористые тела, почвы, грунты
Газообразная	Г/Т	Пористые тела: адсорбенты, катализаторы
Жидкая	Твердая	Т/Ж	Суспензии и золи: илы, пульпы, взвеси, пасты
Жидкая	Ж/Ж	Эмульсии: нефть, молоко, кремы
Газообразная	Г/Ж	Газовые эмульсии и пены
Газообразная	Твердая	Т/Г	Аэрозоли (пыли, дымы), порошки
Жидкая	Ж/Г	Аэрозоли: туманы, облака
Газообразная	Г/Г	Отсутствуют

К о м п о н е н т ы – химические индивидуальные вещества, минимального числа которых достаточно для образования всех фаз системы.

Число независимых компонентов системы, в которой происходят химические взаимодействия, определяется как разность между суммой числа химических соединений, которые могут образоваться в системе в результате взаимодействия индивидуальных веществ и числом химических реакций. Рассмотрим процесс термической диссоциации известняка

СаСО₃ → СаО + СО₂.

Твердыми фазами являются известняк и оксид кальция, газообразная фаза – углекислый газ. Число независимых компонентов системы 3 – 2 = 1, то есть СаСО₃ и СаО, они и являются компонентами системы. Кальций, кислород, углерод тоже слагают все фазы системы, но их число уже не минимальное, и они уже не являются компонентами.

Т е р м о д и н а м и ч е с к и е п а р а м е т р ы – величины, характеризующие состояние системы или термодинамического процесса.

Основными параметрами в физической химии силикатов являются температура, давление, концентрация, объем.

С т е п е н ь с в о б о д ы (f) – независимые термодинамические параметры системы, находящейся в равновесии, которые могут изменять свои значения в некотором интервале без изменения числа и природы фаз.

По числу степеней свободы различают нон(ин)вариантное состояние системы (f = 0), моновариантное (f = 1), би(ди)вариантное (f = 2) и многовариантное состояние.

5.1 Правило фаз

Правило фаз Гиббса (закон равновесия фаз) устанавливает для любых находящихся в равновесии систем соотношение между числом компонентов К, фаз Р и степеней свободы f

f + P = K + 2

Двойка в числе переменных появляется при рассмотрении в качестве независимых параметров температуры и давления.

Для конденсированных систем, к которым относят силикатные системы, состоящих только из жидких и твердых фаз, влиянием давления пара над поверхностью жидкости на протекание термодинамических процессов можно пренебречь, и тогда правило фаз принимает следующий вид f + P = K + 1.

5.2 Диаграмма состояний

Диаграммы состояния представляют собой графическое изображение возможных равновесных состояний в данной системе при различных условиях. Изменения, происходящие в системе, следует рассматривать как последовательность отдельных равновесных состояний, которые достигаются в системе при малом изменении ее параметров.

Диаграммы состояния позволяют установить температуру начала и конца процессов плавления и кристаллизации, состав и количество равновесных фаз при определенной температуре, достижение равновесного состояния или степень отклонения от него.

5.3 Диаграммы состояния однокомпонентных систем

Для однокомпонентной системы согласно правилу фаз максимальная степень свободы равна двум: основными параметрами такой системы являются температура и давление. Общий вид диаграммы ²температура-давление² однокомпонентной системы (рис.14) указывает области существования каждой из фаз в зависимости температуры и давления.

На рис.14 рассмотрен случай, когда компонент А имеет две полиморфные модификации: низко- А₁ и высокотемпературного А₂.

Все области диаграммы являются однофазными: ниже кривой АВСД в системе в равновесии находится пар; выше кривых FCД – жидкость, EBSF – высокотемпературная модификация А₂, АВЕ – низкотемпературная модификация А₁. В границах этих областей можно произвольно менять два параметра: температуру и давлении, без изменения числа и природы фаз.

Например, для состояния системы, обозначенного на рис.14 точкой М, можно в некотором интервале менять температуру (при постоянном давлении минимальной температурой при этом будет температура Тм) или давление или одновременно оба указанных параметра. Степень свободы при этом изменяться не будет, так как не происходит изменения фазового равновесия: сохраняется парообразное состояние вещества А.

Сплошные пограничные линии на диаграмме определяют моновариантное состояние системы: вдоль этих линий в равновесии находятся две фазы.

Так, вдоль кривой АВ в равновесии находятся кристаллы низкотемпературной модификации А₁ и пар, ВС – кр.А₂ + пар, СД – расплав компонента А + пар, ВЕ – кр.А₁ + кр.А₂, СF – кр.А₂ + расплав.

Рис.14. Диаграмма однокомпонентной системы с энантиотропными полиморфными модификациями компонента

Если фазовое равновесие системы описывается точкой, принадлежащей какой либо пограничной линии, то в этом случае произвольно можно изменять только один из параметров: или температуру, или давление. При этом второй параметр будет принимать строго определенное пограничной линией значение. В этом смысле можно говорить о том, что пограничной линией значение. В этом смысле можно говорить о том, что пограничные линии представляют собой графическое изображение функциональных зависимостей давления от температуры (или наоборот) протекания каких-либо фазовых превращений.

Например, пограничная линия ВЕ представляет собой функциональную зависимость давления полиморфного превращения А₁ в А₂ от температуры (в примере давление возрастает с понижением температуры полиморфного превращения).

В системе существует две точки, когда степень свободы равна нулю, т.е. нонвариантное состояние системы. При этом в равновесии находятся одновременно три фазы: точка В (в равновесии кр.А₁ + кр.А₂ + пар) и точка С (кр.А₂ + расплав + пар).

В этих точках невозможно изменять значения термодинамических параметров без изменения числа фаз.

Например: нонвариантное состояние для воды будет определяться значениями температуры +0,01^оС и давления 6,03*10^-3 атм., когда в равновесии будут находиться жидкая вода, лед и водяной пар.

Выше было отмечено, что сплошными линиями на диаграмме указывались стабильные состояния системы. Однако при определенных условиях (как правило, высокие скорости изменения температуры системы) можно получать фазы, существующие некоторый промежуток времени в области стабильного существования другой равновесной фазы.

Например, быстрым охлаждением воды можно фиксировать ситуацию, когда при нормальном давлении вода в жидком состоянии будет существовать при температурах до минус 8^оС, когда равновесной фазой должен быть лед.

Эта ситуация носит название не(мета)стабильного состояния. Термодинамически метастабильное состояние неустойчиво, и такие системы самопроизвольно стремятся перейти в свое стабильное состояние. Однако скорость перехода будет определяться различными факторами и может быть практически незначимой. Из строительных материалов стекла, в том числе силикатные, являются метастабильными системами, существующими длительный промежуток времени в этом состоянии из-за высоких значений их вязкости.

На диаграммах метастабильные состояния указываются пунктирными линиями.

Например, продолжение пограничной линии АВ в область EBCF стабильного существования высокотемпературной модификации А2 (пунктирная линия ВН), определяет метастабильное фазовое равновесии кр.А₁ + пар в области стабильного существования кр.А₂. При этом точка Н, образованная пересечением продолжения линий упругости пара низкотемпературной модификации АВ и упругости пара расплава СД, будет определять температуру плавления низкотемпературной модификации А₁.

Следует отметить, что для неустойчивого метастабильного состояния при фиксированной температуре упругость пара над поверхностью неустойчивой фазы будет всегда больше, чем над поверхностью устойчивой в данных условиях фазы.

Например: при температуре Т_о давление пара над метастабильной высокотемпературной модификацией А₂ будет больше, чем для стабильной А1, т.е. Р_А2 больше Р_А1.

Угол наклона линий зависимости равновесного давления от температуры для различных процессов (например, линия ВЕ) можно определить, используя уравнение Менделеева-Клайперона

P / T = Q / (T*(V₂ – V₁)),

где Q – теплота фазового превращения,

V₁ и V₂ – удельные объемы низко- и высокотемпературных модификаций.

Например, угол наклона кривой зависимости давления фазового перехода воды в лед от температуры будет тупой, так как удельный объем льда будет больше удельного объема воды.

Таким образом, угол наклона будет тупым, если высокотемпературная модификация будет иметь большую плотность: повышение давления при этом снижает температуру фазового перехода.

Для силикатных систем характерным является снижение плотности при повышении температуры и угол наклона кривой будет острым.

5.4 Типы полиморфных превращений

Существует два типа полиморфны превращений: энантиотропные (обратимые) и монотропные (необратимые).

Диаграмма энантиотропных превращений представлена на рис.14, а схема превращений подобного типа приведена ниже.

Отличительными признаками энантиотропных превращений являются:

1. обе полиморфные модификации имеют области стабильного существования на диаграмме;

2. температуры плавления обеих полиморфных модификаций выше, чем температура перехода одной модификации в другую (на рис.14 температура Т₃ больше Т₁ и Т₂).

Диаграмма монотропных превращений показана на рис.15.

Кривые АВ, cД и аF характеризуют соответственно давление насыщенных паров над жидкой фазой, неустойчивой модификации А₂ и устойчивой модификации А₁. Нонвариантная точка а соответствует фазовому равновесию газовой, жидкой и устойчивой А₁ модификации, а точка с – равновесному состоянию газовой, жидкой и неустойчивой А₂ модификации.

Рассмотрим охлаждение исходного состава системы М.

При снижении температуры при постоянном давлении точка М попадает на линию an, где начинается кристаллизация устойчивой формы А₂. При небольших переохлаждениях расплава кристаллизация будет протекать более интенсивно.

Рис.15. Монотропные превращения полиморфных модификаций

Значительное переохлаждение, например до температуры Т₃ при быстром снижении температуры, приводит к кристаллизации неустойчивой модификации А₂, которая в дальнейшем перекристаллизовывается в устойчивую форму А₁.

При монотропных превращениях переход одной модификации в другую необратим.

Невозможность перехода А₁ в А₂ обусловлена тем, что Р₁ > Р₂ (рис.15), а переход в направлении получения формы с большей упругостью пара противоречит первому и второму началам термодинамики.

Переход А₁ в А₂ возможен только путем расплавления неустойчивой модификации и последующим быстрым охлаждением расплава.

Рассмотренные превращения подчиняются правилу последовательных ступеней В.Оствальда: если вещество при данных условиях может образовывать несколько модификаций, то сначала кристаллизуется наименее устойчивая модификация, которая затем переходит в устойчивую через модификации промежуточной устойчивости.

Устойчивая модификация во всех случаях обладает меньшим давлением насыщенного пара, меньшей растворимостью (то есть меньшей химической активностью) и более высокой температурой плавления.

Примерами монотропных превращений могут являться переходы α в β модификации двухкальциевого силиката, превращение ромбического арегонита в тригональный кальцит.

Диаграмма состояния кремнезема

Диаграмма состояния кремнезема отличается сложным полиморфизмом (рис.16). Известны одиннадцать кристаллических полиморфных модификаций и две стеклообразные формы диоксида кремния.

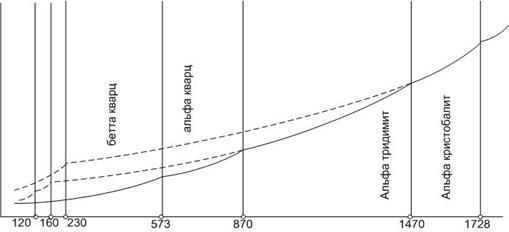
Рис.16. Диаграмма кремнезема с областями равновесных фаз

Кремнезем образует три главные кристаллические модификации: α-кварц, α-тридимит и α-кристобалит. Каждая из этих модификаций имеет, в свою очередь, несколько модификаций второго порядка, представленных на схеме полиморфных превращений кремнезема ниже:

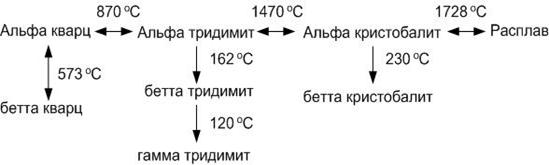
Все кристаллические модификации кремнезема можно разделить на две группы.

В первой группе представлены модификации, имеющие области стабильного существования на диаграмме (сплошные линии на рис.16). Это β- и α-кварц, α-тридимит, α-кристобалит. Пунктирными линиями на диаграмме показаны представители второй группы, не имеющие областей стабильного существования. Превращения внутри главной формы кремнезема (вертикальные ряды схемы полиморфных превращений) происходят быстро из-за незначительной перестройки кристаллической решетки. Превращения между главными формами кремнезема протекают медленно, в течение недель.

Указанные фазовые превращения ускоряются при введении в систему добавок минерализаторов: соединений щелочных и щелочноземельных металлов.

При изготовлении динасовых огнеупоров применяют в основном добавки оксидов кальция и железа.

Механизм действия добавок, вероятно, заключается в ускоряющем действии на процесс фазового перехода за счет появления в системе жидкой фазы, в которой растворяется неустойчивая и кристаллизуется устойчивая в данном температурном интервале полиморфная модификация кремнезема.

Все полиморфные модификации кремнезема сопровождаются изменениями плотности модификаций и, естественно, объемными превращениями.

При переходе от низко- к высокотемпературным формам кремнезема плотность снижается (табл.4). Объемные превращения при фазовых переходах могут достигать 15 и более процентов, что следует обязательно учитывать при проектировании технологических параметров (температура и скорости нагрева или охлаждения) процесса обжига изделий на основе сырья, содержащего кремнезем в свободном состоянии.

Таблица 4 – свойства полиморфных модификаций кремнезема

Полиморфная модификация	Плотность, г/см^3	Полиморфные превращения	Изменение объема, %
α-кварц	2,53	α-кварц ↔ β-кварц	+4,5
β-кварц	2,65	α-кварц ↔γ-кристобалит	+17,4
α-тридимит	2,22
β-тридимит	2,26
γ-тридимит	2,26
α-кристобалит	2,19
β-кристобалит	2,32
расплав	2,20

Диаграмма Феннера (рис.16) имеет больше теоретическое значение, так как на практике повсеместно наблюдаются отклонения от равновесного состояния из-за медленности превращений между главными формами кремнезема и высокой вязкости силикатного расплава.

Отклонения от равновесных состояний в системе кремнезема

1. Поскольку фазовые превращения между главными модификациями происходят очень медленно, при быстром нагревании могут перейти в расплав как α-кварц, так и α-тридимит, при этом температуры плавления этих модификаций ниже (соответственно 1610^оС и 1710^оС), чем у равновесной формы α-кристобалита – 1728^оС.

С другой стороны, α-кристобалит при охлаждении превращается в нестабильный β-кристобалит, а α-тридимит в γ-тридимит, а не в равновесную форму кварца.

2. Расплав кремнезема легко переохлаждается, образуя кварцевое стекло, которое при температуре ниже 1000^оС практически не кристаллизуется.

3. Из кварца при нагревании или кварцевого стекла при расстекловывании в качестве первичной фазы в широком интервале температур стремится выделиться кристобалит называемый метакристобалитом.

Дальнейшие возможные превращения протекают в соответствии с правилом Оствальда. Отклонения от равновесных состояний определяет тот факт, что в технических продуктах обжига (например, динасовом огнеупоре) основными кристаллическими фазами являются метастабильные в обычных условиях тидимит и кристобалит или кремнеземистое стекло.

5.5 Характеристика отдельных полиморфных модификаций кремнезема

Кварц (нем.Quarz) имеет две полиморфные модификации: α-кварц и β-кварц. Природной формой является β-кварц, α-кварц в земной коре не встречается. Обе модификации относятся к каркасным силикатам. Структура α-кварца слагается из тетраэдров [SiO₄], причем все анионы кислорода каждого тетраэдра являются обобществленными. Угол наклона между двумя соседними тетраэдрами (угол связи Si – O – Si) составляет 150^о.

Схематические особенности структуры кварца показаны на рис.17.

Рис.17. Структура кварца.

а – высокотемпературный α-кварц, б – низкотемпературный β-кварц

Группа тетраэдров в структуре кварца располагаются винтообразно вокруг некоторых осей, образуя спирали. В одной спирали тетраэдрами располагаются на разных уровнях: один тетраэдр (1) внизу, другой (2) – в середине и третий (3) – вверху. Эти тетраэдры дают один оборот спирали вокруг оси и затем последовательность слоев повторяется.

В одном кристалле кварца все спирали закручиваются в одну сторону, в другом – могут закручиваться в противоположном направлении. В зависимости от этого различают две формы кварца: левый (вращает плоскость поляризации света влево) и правый.

Структура α-кварца представляет собой несколько искаженную структуру β-кварца. При фазовом переходе происходит небольшое смещение катионов кремния, нарушая симметрию таким образом, что гексагональная ось превращается в тригональную. Сочленение между кремнекислородными тетраэдрами не нарушается.

С химической точки зрения кварц весьма устойчивое вещество. В воде практически нерастворим, из кислот его разрушают только плавиковая и фосфорная. Активнее кремнезем реагирует со щелочами, легко переходя в силикаты при сплавлении со щелочами или карбонатами щелочных металлов. Растворяют кварц также водные растворы едких и углекислых щелочей, особенно при нагревании.

Природный кварц является основным породообразующим минералом литосферы земли. Встречается в самых разнообразных формах: является составной частью многих горных пород, а также месторождений полезных ископаемых самого разнообразного генезиса. Наиболее важные для промышленности кварцевые материалы: кварцевые пески, кварциты (плотные, сцементированные или перекристаллизованные породы из зерен кварца) и кристаллический монокристальный кварц.

К скрытоскристаллическим разновидностям кварца относятся опал и халцедон, яшма и агат, кремень.

Цвет кристаллов, зерен и агрегатов кварца самый разнообразный. Чаще встречаются бесцветные, молочно-белые иди серые разновидности. Прозрачные или полупрозрачные красивоокрашенные кристаллы кварца получили особенные названия: бесцветные и прозрачные – горный хрусталь, фиолетовые – аметист, дымчатые – раухтопаз, черные – морион, золотисто-желтые – цитрин. Различные окраски обусловлены структурными дефектами при замене кремния в структуре тетраэдра на алюминий, железо с одновременным вхождением в кристаллическую решетку натрия, лития или гидроксил иона. В природе встречаются также сложноокрашенные кристаллы за счет микровключений посторонних минералов: золотистый мерцающий авантюрин – включения слюды или гематита.

Применение кварца разнообразно: изготовление строительного и художественного стекла, тонкой керамики (фаянс, фарфор), стеновой керамики, материалов автоклавного синтеза, растворов и бетонов на минеральных и органических вяжущих, огнеупоров различных видов.

Тридимит

Структура тридимита также слагается из кремнекислородных тетраэдров с углом связи в 180^о. Характер связи в α-тридимите предопределяет крупную элементарную ячейку с менее плотной по сравнению с кварцем упаковкой: α и β модификации тридимита имеют структуру с несколько искаженной кристаллической решеткой главной модификации.

В технических и природных продуктах тридимит встречается в качестве продуктов расстекловывания технических стекол, а также образуется при перерождении кварца в динасовых огнеупорах при их длительной эксплуатации.

Кристобалит

Структура кристобалита слагается из кремнекислородных тетраэдров с углам силоксановой связи в 190^о. Атомы кремния в структуре размещаются также, как атомы углерода в алмазе, то есть каждый атом находится в центре группы из четырех соседних атомов. Структура α-кристобалита построена из гексагональных плоских сеток тетраэдров. Сходную, но несколько искаженную структуру имеет β-кристобалит. β-кристобалит встречается в природных породах: опалах, бентонитах, может присутствовать в стеклах как продукт их расстекловывания, в динасе.

Сравнивая структуры модификаций первого порядка следует отметить, что их отличие состоит в разных схемах соединения тетраэдров друг с другом. Разница же между модификациями второго порядка не столь существенна: характер соединения не меняется, а несколько искажается симметрия структуры в результате смещения и вращения тетраэдров без разрыва каких-либо связей.

Модификации кремнезема, не присутствующие на диаграмме Феннера

На поверхности Земли или на незначительной глубине основной формой кремнезема, как мы уже отмечали, является кварц. Однако поиски иных форм кремнезема были связаны в первую очередь с тем, что температура и давление на глубине достигают высоких значений и это может приводить к качественным изменениям в структуре силикатов, основных породообразующих минералов. Экспериментируя с воздействием на кремнезем температурой и давлением были получены следующие модификации кремнезема: коэсит, китит, стишовит.

В исследованиях при высоких давлениях, предпринятых в США Л.Коэсом (Coes) в 1953 г, была получена при давлении около 3 ГПа новая фаза кремнезема, впоследствии названная коэситом. Плотность ее 3,01 г/см³. Это выше, чем у кварца, но анализ структуры показал, что кремний сохраняет в ней обычную координация по отношению к кислороду.

В 1961 г. молодые русские исследователи С.М.Стишов и С.В.Попова получили новую модификацию кремнезема (при давлениях 16 … 18*10⁴ кг/см² и температуре 1200 … 1400^оС), названную стишовитом. Изучение физико-химических свойств стишовита показало, что его плотность, равная 4,35 г/см³ на 64% больше, чем у кварца, что объясняется изменением координации кремния с 4 на 6 по отношению к кислороду. Стишовит полностью устойчив к плавиковой кислоте, но хорошо растворяется в расплавах и растворах щелочей.

Кремнеземистое стекло

Кремнезем в виде стекла встречается в природе, а также легко получается искусственным путем. Обычное кремнеземистое стекло является наименее плотной формой кремнезема, обладая при этом рядом замечательных свойств:

- высокая химическая стойкость. Стойкость против действия всех кислот, за исключением плавиковой и ортофосфорной;

- низкий коэффициент термического расширения (КЛТР = 0,6*10^-6 1/град);

- способность к пропусканию ультрафиолетовых лучей;

- высокая огнеупорность;

- высокая упругость.

При длительной эксплуатации при высоких температурах (1000^оС) кремнеземистое стекло может расстекловываться (кристаллизовываться), выделяя в кристаллической фазе α-кристобалит. Расстекловывание само по себе не приводит к разрушению изделий, так как объемные деформации при этом невелики. Однако, если после длительной работы при высоких температурах изделие охладить ниже 150 … 275^оС, оно может разрушиться под воздействием напряжений, возникающих при фазовом переходе α → β-кристобалит.

5.6 Диаграммы состояния двухкомпонентных систем

При наличии в системе двух компонентов фазовые превращения усложняются: наряду с фазовыми превращениями, полиморфными модификациями компонента могут происходить и другие процессы, обусловленные взаимодействием компонентов.

Это определяет многообразие типов диаграмм систем с двумя компонентами. Рассмотрим сначала основные типы диаграмм, а затем некоторые диаграммы силикатных систем, практически применяемых в производстве вяжущих веществ, керамики, огнеупоров и некоторых других строительных материалов.

5.6.1. Диаграмма двухкомпонентной системы с одной точкой эвтектики

Для конденсированных систем, содержащих два компонента, максимальное число степеней свободы равно двум. При этом в качестве независимых термодинамических параметров принимают температуру и концентрацию первого компонента [С₁]. Концентрация второго компонента [C₂] рассчитывается по формуле: С₂ = 100 – С₁. Вертикальная ость диаграммы – ось температуры, горизонтальная ось – ось концентрации компонентов.

Внешний вид диаграммы приведен на рис.18. Левый конец горизонтальной оси концентраций компонентов, обозначенный буквой А, соответствует 100% содержанию компонента А, правый – 100% содержанию компонента В.

Рассмотрим основные элементы диаграммы.

Та и Тв – соответственно температуры плавления чистых компонентов А и В. Если точка состава находится на одной из вертикальных осей диаграммы (на А или В), то в этом случае мы рассматривает процессы, происходящие в однокомпонентной системе.

Кривые Та-Е и Е-Тв носят название кривых ликвидуса.

Кривые ликвидуса представляют собой температурные зависимости перенасыщения расплава по отношению к какому-либо компоненту или химическому соединению. Кривая Та-Е показывает температуру начала кристаллизации в системе компонента А из расплава при его охлаждении, кривая Е-Тв – соответственно начала кристаллизации компонента В.

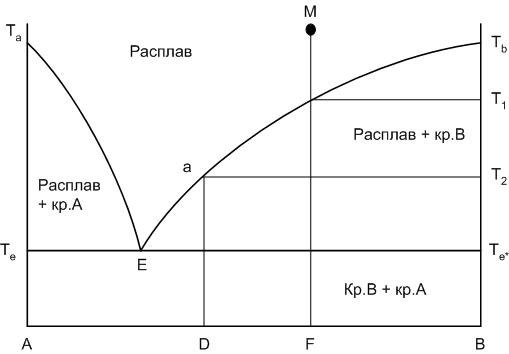
Рис.18. Диаграмма двухкомпонентной системы

Точка Е носит название точки эвтектики и характеризует состав расплава с минимальной для данной системы температурой существования жидкой фазы: расплав эвтектического состава. Этот расплав пересыщен одновременно по отношению к обоим компонентам А и В. При кристаллизации расплава эвтектического состава компоненты выделяются в твердой фазе всегда в строго определенном соотношении, определяемом положением точки эвтектики.

Линия Те-Е-Те* носит название линии солидуса. Это линия окончания кристаллизации или начала плавления любого бинарного состава системы. Ниже линии солидуса в равновесии могут находиться только фазы в твердом состоянии. Следует также отметить, что линия солидуса не всегда горизонтальна.

Диаграмма равновесия позволяет определять последовательность фазовых превращений в системе при ее нагреве или охлаждении, фазовые равновесия при любых параметрах системы, рассчитывать количественное соотношение равновесных фаз при заданных условиях равновесия.

Рассмотрим последовательность фазовых превращений, происходящих при охлаждении исходного состава системы М (рис.18). Следует отметить, что если рассматривать нагрев исходного состава системы М, то последовательность фазовых превращений будет обратной его охлаждению, поэтому в дальнейшем мы будем рассматривать только кристаллизацию исходных составов.

Итак, начинаем охлаждать с постоянной скоростью расплав, соотношение компонентов в котором определяется точкой М.

Выше температуры Т₁ в равновесии находится расплав Lm состава М. Число степеней свободы при этом равно двум: можно в некоторых пределах изменять температуру и состав системы (добавляя, например, в расплав кристаллы одного из компонентов, которые сразу же плавятся) без изменения фазового равновесия.

Указанное фазовое равновесие будет наблюдаться при охлаждении до температуры Т₁. При температуре Т₁, когда вертикаль исходного состава касается линии ликвидуса, расплав становится пересыщен по отношению к компоненту В, и начинается его кристаллизация. Так как степень свободы при этом становится равной единице, то при дальнейшем охлаждении при продолжающейся кристаллизации компонента В состав расплава будет меняться строго по линии ликвидуса.

Например, при температуре Т₂ расплав будет иметь состав, определяемый положением точки а на линии ликвидуса Е-Тв.

Таким образом, на диаграмме в области, ограниченной точками Е-Тв-Те* в равновесии будут находиться две фазы: кристаллы компонента В и расплав, состав которого зависит от рассматриваемой температуры системы.

Горизонтальная линия, проведенная при температуре Т2 от линии ликвидуса до вертикали выпадающей твердой фазы, носит название конноды.

При достижении температуры эвтектики состав расплава становится равным Lm и начинается кристаллизация компонента А. В равновесии будут находиться уже три фазы: расплав, кристаллы А и В. Степень свободы при этом становится равной нулю. Таким образом, точка эвтектики на диаграмме определяет нонвариантное состояние. Дальнейшее понижение температуры невозможно без изменения числа равновесных фаз. Поэтому в точке эвтектики закончится кристаллизация исходного состава системы, а пропадающей фазой при этом будет расплав. По окончании кристаллизации система становится моновариантной, и дальнейшее понижение температуры приводит к охлаждению смеси кристаллов А и В.

Фазовые изменения любого другого бинарного состава системы будут протекать аналогично рассмотренному. Исключение составляет исходный состав, совпадающий с точкой эвтектики. Для него при температуре Те начинается одновременная кристаллизация компонентов А и В и при этой же температуре кристаллизации закончится.

Фазовые изменения исходного состава системы М или его путь кристаллизации удобно представить в виде (табл.5).

В таблице запись Lm- > е следует понимать так: состав расплава меняется от точки М к точке е. Для определения состава расплава, как и любой другой точки системы из искомой точки опускается перпендикуляр на ось концентраций: точка пересечения этих прямых

Таблица 5 – фазовые изменения системы при охлаждении

Температура	Равновесные фазы	Степень свободы
Т = То	Lm
Т = Т1	Lm + кр.В
Те < Т < Т1	Lm- > е + кр.В
Т = Те	Lе + кр.А +кр.В
Т < Те	кр.А + кр.В

определяет соотношение компонентов в расплаве.

Для упрощения записей в дальнейшем по тексту лекций мы не будем употреблять для записи кристаллической фазы сокращение [кр.], а только наименование компонента (А или В) или химического соединения, например АВ.

5.6.2. Правило рычага

По диаграммам равновесия двухкомпонентных систем можно определять не только качественно фазовые равновесия, но и рассчитывать количественное соотношение равновесных фаз.

Для этого используется правило рычага: если одна фаза в системе распадается на две, то количество образовавшихся фаз обратно пропорционально отрезкам, заключенным между точкой исходного состава и точками составов образовавшихся фаз.

Покажем работу правила на примере. Пусть Q – масса исходного расплава состава М (рис.18). При охлаждении исходного состава до температуры Т₂ выделилось некоторое количество кристаллов компонента В. Обозначим это количество кристаллов через Х.

В исходном расплаве при температуре выше Т₁ количество компонента А определяется как

А = (Q*FB) / 100

При температуре Т₂ количество компонента А в расплаве определяется как

А = (Q – X)*DB / 100.

Учитывая, что при кристаллизации исходного расплава до температуры Т₂ количество компонента А не изменялось, мы вправе записать

(Q*FB) / 100 = (Q – X)*DB / 100

Из последнего уравнения имеем количество кристаллов как

X = Q*(DB – FB) / DB = (Q*DB) / DB

и количество расплава

Q – X = (Q*FB) / DB.

Отношение равновесных фаз при температуре Т₂ (кристаллов к расплаву) будет определяться следующим образом:

X / (Q – X) = (Q*DF*DB) / (DB*Q*FB) = DF / FB.

Таким образом, отрезок DB определяет общее количество равновесных фаз, отрезок DF – количество кристаллической фазы, FB – количество оставшегося в системе расплава.

Для практического использования правила рычага при решении задач фазового равновесия необходимо за 100% принять отрезок, ограниченный составами равновесных в данных условиях фаз. Точка исходного состава будет обязательно находиться на этом отрезке и делить его в пропорциях, соответствующих равновесным фазам.

5.6.3. Построение диаграмм состояния

Построение равновесных диаграмм основано на изучении количества и состава фаз при различных температурах. Для таких целей используют два метода: динамический (метод кривых охлаждений) и статический (метод закалки).

Суть динамического метода заключается в построении кривых охлаждения (нагревания) для исходных составов системы в координатах ²температура-время² при постоянной скорости изменения температуры. При этом с помощью специального оборудования обнаруживаются тепловые эффекты, вызываемые физико-химическими процессами, происходящими в системе: полиморфные превращения, химические реакции, кристаллизация и плавление, разложение соединений системы.

Построение диаграммы равновесия двухкомпонентной системы А-В заключается в анализе кривых охлаждения (рис.19). Для этого составляют смеси компонентов А и В при их различном соотношении и нагревают навеску до полного ее плавления. Получаемый расплав выдерживается для достижения полной гомогенизации, а затем охлаждается с постоянной скоростью и фиксированием температуры смеси во времени.

Если рассматривается точка, содержащая 100% компонента (кривые А или В), то на кривой охлаждения появляется горизонтальная площадка кристаллизации, температура которой соответствует температуре кристаллизации данного компонента. Число степеней свободы при этом равно 0, то есть пока не изменится число фаз (в равновесии находятся одновременно расплав компонента и его кристаллы) температура системы изменяться не может. Если мы рассматриваем процесс охлаждения системы, то после окончания кристаллизации (расплав пропадает) в равновесии будет находиться только одна фаза – кристаллы, и температура навески начнет понижаться. На диаграмму находятся соответственно точки кристаллизации компонентов А и В на вертикалях, соответствующих 100% содержанию каждого из них (ta и tв).

Рис.19. Построение диаграмм равновесия по кривым охлаждения

Если охлаждается смесь компонентов (например, состав 1, в котором содержание компонента А = 80%, а компонента В = 20%), то при какой-то температуре расплав становится перенасыщенным по отношению к одному из них. Начинается кристаллизация компонента (в нашем примере компонента А). Так как процесс кристаллизации носит экзотермический характер, то выделяющееся при этом тепло уменьшает скорость охлаждения системы и на кривой охлаждения это фиксируется появлением угла наклона.

Точка перегиба проецируется на вертикаль исходного состава диаграммы. Аналогично наносятся другие точки составов, принадлежащие кривым ликвидуса диаграммы.

Для всех смесей при температуре эвтектики появляется площадка кристаллизации, когда происходит кристаллизация расплава эвтектического состава. Величина горизонтальной площадки, соответствующей этому процессу, будет зависеть от исходного состава системы и будет максимальна для состава Е. Указанное выше положено в основу построения треугольника Таммана для определения точного положения некоторых точек диаграммы. В нашем случае перпендикулярно эвтектической горизонтали для каждого состава системы откладывается длина горизонтальных площадок h₁, h₂, h₃, h₄, через концы которых проводят прямые линии. Их взаимное пересечение указывает на точное положение эвтектического состава системы.

Анализ кривых охлаждения позволяет установить также положение на диаграмме линий полиморфного превращения, химических соединений, точек эвтектики и перитектики.

Для силикатных систем, скорость установления равновесного состояния в которых невелика, динамический метод дает не всегда корректный результат. В этом случае пользуются статическим методом: гомогенизированную смесь компонентов нагревают до заданной температуры, выдерживают длительное время при этой температуре, а затем резко охлаждают. Затем методами химического анализа проводят определение состава и количества образовавшихся фаз. Эта процедура для одного состава многократно повторяется при изменении температуры выдержки и по полученным результатам строят диаграмму равновесия. Метод отличается высокой точностью, но большей, чем в динамическом методе, трудоемкостью.

5.6.4. Диаграмма состояния двухкомпонентной системы с химическими соединениями

Зачастую между компонентами системы наблюдается химическое взаимодействие с образованием химических соединений. Рассмотрим такие типы диаграмм. На рис.20 представлены диаграммы равновесия со всеми типами химических соединений: плавящимися конгруентно (без разложения) – AmBn, инконгруентно (с разложением) – АВ и разлагающимся в твердой фазе – ApBq.

Составы химических соединений на диаграмме показываются сплошными вертикальными линиями, проведенными из точки соотношения компонентов в химических соединениях.

Так как соединение AmBn плавится конгруентно, то состав его соответствует составу расплава, получаемого при плавлении соединения, то есть линия состава химического соединения обязательно доходит до линии ликвидуса при температуре плавления химического соединения. Диаграмма по линии соединения AmBn делится на две части, каждая из которых представляет собой отдельную диаграмму. В этом смысле никаких отклонений в кристаллизации исходных составов системы от ранее рассмотренных не будет. Если исходный состав системы соответствует составу химического соединения, то кристаллизация его начнется и закончится при температуре

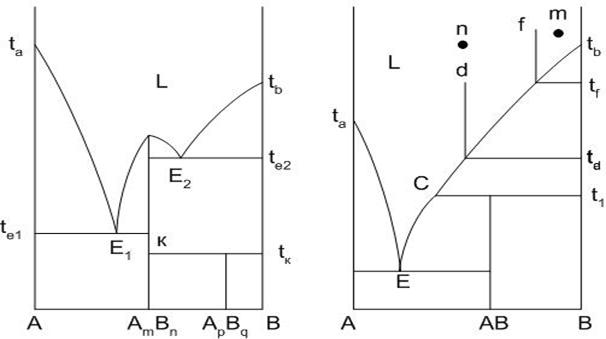
Рис.20. Диаграммы равновесия двухкомпонентных систем с химическими соединениями

плавления химического соединения AmBn (как для отдельного компонента).

Вертикальная линия состава химического соединения ApBq, разлагающегося в твердой фазе при нагревании доходит до горизонтальной линии к – t_k, проведенной при температуре разложения ApBq. Концы линии указывают на составы образующихся при разложении химического соединения ApBq фаз (точка к – кристаллы химического соединения AmBn, точка t_к – кристаллы компонента В).

Отличительной особенностью диаграммы с химическим соединением, плавящимся инконгруентно, является то, что вертикаль состава химического соединения АВ не доходит до линии ликвидуса E-C-tв. При температуре Т₁ при нагревании химическое соединение плавится с разложением на расплав состава Lc и кристаллы компонента В, при этом состав расплава не соответствует составу химического соединения (точка состава расплава С и вертикаль химического соединения не совпадают).

Точка С на диаграмме – точка перитектики. Эта точка, в которой начинается и протекает химическая реакция взаимодействия ранее выделившегося в кристаллическом состоянии компонента В и расплава Lc с образованием химического соединения АВ: кр.В + Lc = AB. В точке перитектики в равновесии находятся одновременно три фазы, определяющиеся нонвариантное состояние системы. Пока одна из фаз не исчезнет, температура изменяться не может. Какая фаза пропадает в результате протекания химической реакции, зависит от точки исходного состава системы. Если исходный состав системы содержит компонента В больше, чем его находится в химическом соединении АВ (точка М на рис.20), то в результате протекания химической реакции в точке перитектики пропадет расплав, в равновесии останутся две кристаллические фазы: АВ и В. Если исходный состав системы содержит компонента В меньше, чем его находится в химическом соединении АВ (точка N на рис.20), то в результате протекания химической реакции в точке перитектики пропадет компонент В, в равновесии останутся расплав состава С и АВ. И в том случае, когда в исходном составе системы количество компонента В совпадает с его количеством в химическом соединении, то в результате протекания химической реакции в точке перитектики пропадут как В, так и расплав: в равновесии останутся только кристаллы химического соединения АВ. Пути кристаллизации исходных составов системы приведены в табл.6.

Таким образом, кристаллизация исходных составов системы может закончиться как в точке эвтектики, так и в точке перитектики.

Таблица 6

Температура	Равновесные фазы	Примечание
Состав а:
T > Ta	La
T = Ta	La + кр.В
T1 < T < Ta	La→c + кр.В
T = T1	Lc + кр.В = AB	Начало химической реакции, в резуль- тате которой исчезает В
T < T1	Lc + AB
и далее по диаграмме
Состав в:
T > Tв	Lв
Т = Тв	Lв + кр.В
Т1 < T < Тв	Lв > c + кр.В
T = T1	Lc + кр.В = AB	Начало химической реакции, в резуль- тате которой исчезает Lc
T < T1	B + AB
и далее по диаграмме

5.8.5. Диаграмма состояния двухкомпонентной системы с явлением ликвидации

Ликвация – расслоение жидкости на две, каждая из которых имеет свой состав и свои свойства.

Внешний вид диаграммы показан на рис.21. Область концентраций, для которых наблюдается явление ликвации, ограничена кривой F-L₁-L₂-G. Пути кристаллизации составов данной диаграммы приведены в табл.7.

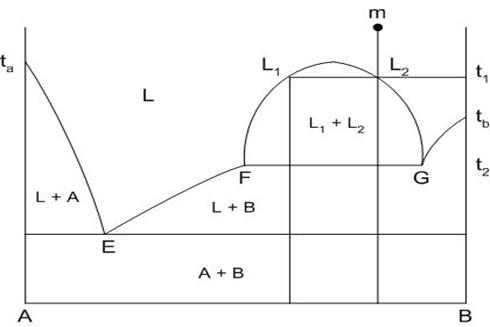Рис.21. Диаграмма состояния двухкомпонентной системы с явлением ликвации

Таблица 7 – фазовые изменения в системах с лиувацикй

Температура	Равновесные фазы	Примечание
Состав m:
T = T1	L1 + L2	Расслоение жидкой фазы на две
T2 < T < T1	L1→f + L2→g
T = T2	Lf + Lg + B	Кристаллизация В идет из расплава Lg
Te < T < T2	Lf→e + B
T = Te	Le + B + A
T < Te	B + A

Кристаллизация компонента В при температуре Т₂ идет из расплава, который содержит в себе большее количество этого компонента, то есть из расплава G, состав которого меняется по прямой GF к точке F. В точке F составы расплавов сравниваются и ликвация как явление пропадает.

5.8.6. Диаграммы состояния двухкомпонентных систем с твердыми растворами

Если содержащиеся в твердом растворе компоненты могут смешиваться в любых соотношениях, то мы имеем дело с твердыми растворами неограниченной растворимости или непрерывным рядом твердых растворов (рис.22).

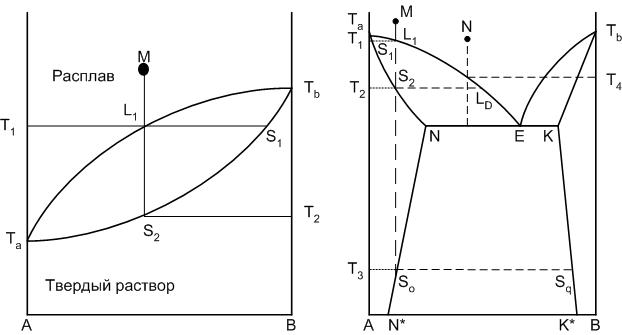
Рис.22. Диаграммы равновесия двухкомпонентных систем с твердыми растворами

При наличии однофазного твердого раствора из двух компонентов, находящегося в равновесии с расплавом, состоящим их тех же компонентов, степень свободы системы будет равна единице, то есть каждой температуре соответствует строгая концентрация компонентов в твердом растворе и расплаве. На диаграмме появляется кривая, показывающая изменение состава твердой фазы при изменении температуры (кривая Та-S₁-Тв). Составы равновесных расплава и твердого раствора определяются концами конноды, проведенной при заданной температуре, например между точками L₁ и S₁. Когда точка М достигнет линии ликвидуса, начинается кристаллизация твердого раствора S₁. При дальнейшем понижении температуры состав жидкости меняется по кривой ликвидуса, состав твердого раствора – по кривой солидуса. При температуре Т₂, когда состав твердого раствора совпадает с исходным составом системы, кристаллизация закончится. Изменение состава твердого раствора в процессе кристаллизации происходит за счет диффузии атомов или ионов одного компонента в кристаллической решетке.

Если смешиваемость компонентов происходит лишь до некоторых пределов концентраций, то такой твердый раствор называется твердым раствором с ограниченной растворимостью. При эвтектической температуре в равновесии с расплавом находятся два твердых раствора: α и β. Точки N и К – точки предельной концентрации твердых растворов, которая изменяется при понижении температуры по линиям предельной растворимости (например, для твердого раствора α линия предельной растворимости компонентов А и В – N-N*).

На диаграмме составов, пути кристаллизации которых отличаются друг от друга, можно выделить три интервала: А-N*, N*-N, N-E, если рассматривать точку эвтектики как точку симметрии диаграммы. Пути кристаллизации составов, находящихся в интервале A-N*, не отличаются от путей кристаллизации составов с твердыми растворами неограниченной растворимости (рис.22 а). Пути кристаллизации других составов системы приведены в табл.8.

Таблица 8 – фазовые изменения в системах с твердыми растворами

Температура	Равновесные фазы	Примечание
Состав m:
Т = Т1	L1 + тв.р-р	Состав твердого раствора – S1
Т→Т2	L(1→D) + S(1→2)
Т = Т2	тв.р-р (S2)	Кристаллизация закончилась
Т = Т3	тв.р-р (So)^+ тв.р-р (Sq)	Разделение в твердой фазе на два раствора
Т < Т3	тв.р-р (So- > n*) тв.р-р (Sq- > k*)	Изменение концентрации твердых растворов по линиям предельной растворимости
Состав n:
Т = Т4	тв.р-р (S4) + расплав L4	(составы условно не показаны)
Т = Те	тв.р-р (Sn)^+ тв.р-р (Sk)^+	Кристаллизация закончилась
Т < Те	тв.р-р (Sn- > n*) тв.р-р (Sk- > k*)	Изменение составов твердых растворов

5.7 Практическое значение диаграмм состояния уравнения двухкомпонентных систем

Для производства строительных материалов большое значение имеют составы исходных смесей, подобранные на основе диаграмм двухкомпонентных систем СаО – SiO₂, CaO – Al₂O₃, Al₂O₃ + SiO₂ и ряда других. Рассмотрим подробнее указанные системы.

5.8.1. Система CaO – SiO₂

Система имеет важное техническое значение при производстве портландцементного клинкера и цементов на его основе. Диаграмма системы показана на рис.23.

В данной системе существуют четыре химического соединения: C₃S, C₂S, C₃S₂, CS.

Метасиликат кальция CaO*SiO₂ (CS). Структура минерала относится к цепочечным силикатам Ca[SiO₃]. Минерал имеет две полиморфные модификации: α-CS и β-CS.

Высокотемпературная модификация: псевдоволлостанит α-CS встречается в продуктах кристаллизации стекол и шлаков. Природный воллостанит β-CS кристаллизуется из стекол при температуре 1000^оС в виде длинных иголок.

Трехкальциевый дисиликат 3CaO*2SiO₂: Ca₃[Si₂O₇]. Минерал плавится инконгруентно при температуре 1364^оС, разлагаясь на белит и расплав состава 44,5% кремнезема и 55,5% CaO. В природе встречается в виде редкого минерала ранкинита: обнаружен в некоторых технических продуктах, например в доменных шлаках.

Двухкальциевый силикат 2CaO*SiO: Ca₂[SiO₃]. Минерал относится к ортосиликатам кальция. Главная структурная особенность ортосиликата кальция – склонность к образованию полиморфных модификаций (рис.24).

Три из четырех полиморфных модификаций имеют область стабильного существования. Метастабильная форма отросиликата кальция – β модификация не имеет при нормальном давлении температурной области устойчивого существования, но может существовать при определенных условиях при температуре ниже 675^оС.

Все превращения, за исключением β → γ, носят энантиотропный характер. При охлаждении расплава сначала кристаллизуется α-C₂S, переходящая при понижении температуры в α’-C₂S. Теоретически при дальнейшем охлаждении должен кристаллизоваться γ-C₂S, однако на практике реализуется правило Оствальда: последовательность полиморфных модификаций α → β → γ. Это объясняется меньшими структурными изменениями системы при переходе α → β.

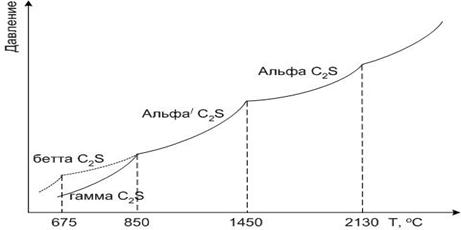Рис.24. Схема полиморфных превращений двухкальциевого силиката

Для всех модификаций ортосиликата кальция характерно то, что они построены из независимых кремнекислородных тетраэдров, связанных между собой катионами кальция с координационным числом 6 … 9.

Плотность α-C₂S составляет 3,28 г/см³, плотность β-C₂S – 2,97 г/см³; указанный выше переход сопровождается расширением системы на 12% и самопроизвольным переходом минерала в тонкодисперсное состояние. Этот процесс носит название «силикатный распад».

Модификация, в которой ортосиликат кальция присутствует в технических продуктах, оказывает решающее значение на их свойства. Только нестабильный β-C₂S обладает гидравлической активностью и является основным минералом портландцементного клинкера. Поэтому на практике при производстве цемента необходимо получить ортосиликат кальция в виде его метастабильной модификации, предотвратив переход β-C₂S в γ-C₂S.

Указанная стабилизация может осуществляться различными способами. Одним из них является кристаллохимическая стабилизация, основанная на образовании ортосиликатом кальция твердых растворов с оксидами бария, хрома, фосфора, которые вводятся в состав шихты в количестве до 1%.

Другая форма стабилизации – понижение температуры термической обработки сырья до 1050 … 1100^оС, а также быстрое охлаждение клинкера, когда не происходит перегруппировка атомов кристаллической решетки. Кроме того, быстрое охлаждение сохраняет в продуктах обжига стекловидную фазу, обволакивающую зерна ортосиликата кальция и механически препятствующую их расширению.

γ-C₂S, стабильный при нормальных температурах, не обладает гидравлической активностью: небольшое количество ионов-сульфатов и ионов хлора усиливают его вяжущие свойства.

Трехкальциевый силикат 3CaO*SiO₂: Ca₃[SiO₅]. Основной минерал портландцементного клинкера, представленный в нем в виде твердого раствора C₃S с оксидами алюминия и магния. Чистый C₃S разлагается ниже температуры 1250^оС на отросиликат кальция и СаО. Распад трехкальциевого силиката предотвращается резким охлаждением, поэтому при комнатной температуре минерал находится в метастабильном состоянии, что усиливает его вяжущие свойства.

5.8.2. Система Al₂O₃ – SiO₂

На рис.25 приведена диаграмма состояния диаграмма состояния системы Al₂O₃ – SiO₂ по Н.А.Торопову и Ф.Я.Галахову. Согласно этой диаграмме химическое соединение 3Al₂O₃*2SiO₂ – муллит плавится конгруентно при температуре 1910^оС и имеет две эвтектики: одну с кремнеземом при температуре 1585^оС, другую с твердым раствором глинозема в муллите и глиноземом при 1850^оС. Область твердых растворов муллита с глиноземом находится в пределах 71,8 … 78% Al₂O₃.

Особенностью диаграммы является пологий характер кривой ликвидуса Е1-С, что свидетельствует о быстром нарастании количества жидкой фазы при нагревании и быстрой кристаллизации при охлаждении.

Муллит редко встречается в природе, в основном как продукт действия огненно-жидких лав на глинистые породы. Чаще муллит встречается в составе технических силикатов: алюмосиликатных огнеупоров, фарфора, строительной керамики и т.п. как конечный продукт обжига глин и каолинов:

3(Al₂O₃*2SiO₂*2H₂O) → 3Al₂O₃*2SiO₂ + 4SiO₂ + 6H₂O.

Муллит обладает высокой химической стойкостью и огнеупорностью.

На основе диаграммы приготавливаются составы шихты для производства шамотных, муллитовых, корундовых и динасовых огнеупоров, муллитовой и корундовой технической керамики.

Шихта с содержанием 0,2 … 1,0% оксида алюминия является сырьем для производства динасовых (кремнеземистых) огнеупоров. Их огнеупорность составляет 1730^оС, механическая прочность 15 … 35 МПа. Изделия обладают малой термической стойкостью и используются для кладки сводов и стен мартеновских и стекловаренных печей.

При 40 … 60% глинозема в составе шихты она используется для производства шамотных огнеупоров, характеризующихся высокой термической стойкостью.

Высокоглиноземистые огнеупоры (температура огнеупорности до 2000^оС) содержат в составе шихты от 60 до 90% оксида алюминия. Плавленый корунд (Al₂O₃ до 99%) получают путем высокотемпературного обжига технического глинозема. Корундовые огнеупоры обладают высокой химической стойкостью, стойкостью против абразивного воздействия и эрозии.

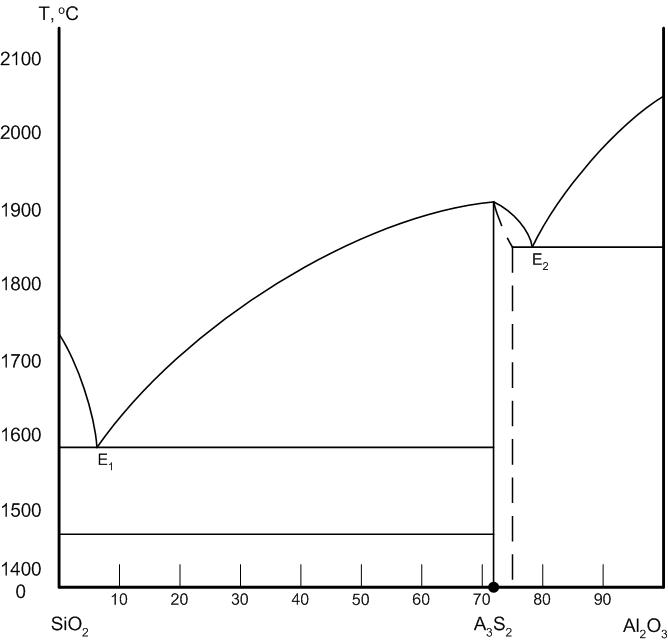
Рис.25. Диаграмма Al₂O₃ – SiO₂

5.8.3. Система CaO – Al₂O₃

Диаграмма, представленная на рис.26, не отностится к силикатным системам, но используется в производстве портландцемента, глиноземистого и высокоглиноземистого цементов, технической керамики.

В системе существуют пять химических соединений: С₃А, С₅А₃, СА, СА₂, СА₆.

Трехкальциевый алюминат 3CaO – Al₂O₃ – один из минералов портландцементного клинкера, имеет высокую гидравлическую активность, обеспечивает быстрое твердение цемента, ответственен за долговечность изделий на основе портландцемента.

Минерал 5CaO –3 Al₂O₃ содержится в составе глиноземистого цемента, обладая малой гидравлической активностью. Состав минерала иногда в технической литературе изображают формулой С₁₂А₇.

Моноалюминат кальция CaO – Al₂O₃ – основной минерал глиноземистого цемента. Образует твердые растворы с оксидами железа и других металлов. Обладает высокой скоростью взаимодействия с водой.

Минерал CaO – 2Al₂O₃ содержится в небольших количествах в глиноземистом и является основным минералом высокоглиноземистого цемента.

CaO – 6Al₂O₃ – малоизученное соединение, найденное в плавленом корунде.

Рис.26. Диаграмма CaO – Al₂O₃

Контрольные вопросы

1. Что представляет собой диаграмма двухкомпонентной системы?

2. Какие термодинамические параметры системы являются независимыми?

3. Назовите и дайте краткую характеристику элементов диаграммы двухкомпонентной системы?

4. Определите условия, при которых кристаллизация исходных составов системы заканчивается в точке перитектики.

5. С какой целью на диаграммах используется правило рычага? Сформулируйте это правило.

6. Рассмотрите путь кристаллизации исходного состава N на рис.20.

7. Дайте характеристику минералов в системе CaO – SiO₂, CaO – Al₂O₃, SiO₂ – Al₂O₃. Расскажите о строительных материалах, в основе производства которых находятся эти диаграммы.

8. Какими способами можно обеспечить стабилизацию силикатных минералов портландцементного клинкера?

9. Можно ли огнеупор состава 30% SiO₂⁺ 70% Al₂O₃ нагревать до температуры 1700^оС?

Основная литература [13], дополнительная литература [1, 2].

5.8 Диаграммы состояния трехкомпонентных систем

Для трехкомпонентых систем согласно правилу Гиббса максимальная величина числа степеней свободы равна 3. При этом в качестве независимых параметров выступают температура, концентрация первого С1 и второго С2 компонентов. Концентрация третьего компонента зависит от первых двух: С3 = (100 - С1 – С2).

Диаграмма является пространственной фигурой: концентрации компонентов откладываются на сторонах равностороннего треугольника (треугольника концентраций), а температура – на перпендикуляре, проведенном к плоскости треугольника концентраций (рис.27).

В целом диаграмма представляет собой призму, грани которой образованы соответствующими двухкомпонентными диаграммами.

На диаграмме трехкомпонентной системы вместо линий появляются поверхности ликвидуса, например: А*-Е1*-Е*-Е3*-А*, С*-Е2*Е-Е3*-С*, В*-Е1*-Е*-Е2*-В*, при пересечении которых образуются пограничные кривые Е1*-Е*, Е2*-Е*, Е3*-Е, сходящиеся в точке тройной эвтектики Е*. Поверхность ликвидуса имеет те же свойства, что и кривая ликвидуса: показывает температуру начала кристаллизации (конца плавления) любого состава системы; состав насыщенной жидкой фазы находится в равновесии с твердой фазой при данной температуре.

Для удобства работы пользуются проекционными диаграммами, которые образуются при проецировании на плоскость треугольника концентраций всех элементов строения пространственной диаграммы. Температура на диаграмме показывается в этом случае изотермами, получаемыми пресечением пространственной диаграммы плоскостями, параллельными треугольнику концентраций при фиксированном значении температуры. Часто изотермы на проекционной диаграмме не показываются вообще, чтобы не усложнять изображение.

Рис.27. Пространственная диаграмма трехкомпонентной системы

Пограничные линии разделяют треугольник концентраций на поля первичной кристаллизации соединений, существующих в данной системе. Например, на рис.28 поле Е₁-В-Е₂-Е-Е₁ – поле первичной кристаллизации компонента В, А-Е₁-Е-Е₃-А – компонента А и С-Е₃-Е-Е₂-С – компонента С.

Состав кристаллов в поле первичной их кристаллизации отмечается кружком.

Рис.28. Проекционная диаграмма трехкомпонентной системы

Точки составов двойных соединений находятся на сторонах треугольника, точки составов тройных химических соединений – внутри его. Точки составов химических соединений или компонентов системы, имеющие смежные поля первичной кристаллизации, соединяются тонкими прямыми линиями, носящими название соединительных прямых. Соединительные прямые разбивают всю диаграмму на отдельные элементарные треугольники, каждый из которых может рассматриваться как отдельная диаграмма трехкомпонентной системы.

Вершина проекционного треугольника соответствует 100% содержанию компонента, название которого находится у данного угла. Если точка состава находится на стороне треугольника, то ее количественный состав определяется как для двухкомпонентной системы, например состав точки Е₁ на рис.28 содержит 60% компонента В и 40% компонента А. Если точка исходного состава находится внутри треугольника, то ее состав можно определить следующим образом. Через точку (точка М на рис.28) проводятся прямые, параллельные сторонам проекционной диаграммы. Прямые рассекают каждую строну проекционной диаграммы на три отрезка, каждый из которых определяет количественное содержание одного из компонентов. Например, для стороны СВ отрезок Сс определяет количество компонента В в точке М, отрезок cd – количество компонента А и отрезок dB – количество компонента С. Несложно геометрически доказать, что стороны треугольника разбиваются на три равных по величине отрезка и безразлично, на какой из сторон проводить определение. В общем случае необходимо помнить, что средний отрезок определяет количество компонента противоположного угла диаграммы, а отрезки, примыкающие к углам диаграммы, определяют количество компонентов, принадлежащих данной стороне в обратной пропорции. Это правило будет работать и в том случае, когда рассматриваемая диаграмма не является равносторонним треугольником (например, рассматривается элементарный треугольник какой-либо трехкомпонентной системы). При этом длину стороны, на которой проводятся определения, следует принять за 100%, рассчитав затем процентное содержание каждого компонента.

Для успешной работы с диаграммами трехкомпонентных систем необходимо освоить ряд правил, которые будут излагаться ниже по ходу рассмотрения различных типов диаграмм.

5.9 Диаграмма состояния трехкомпонентной системы с точкой тройной эвтектики

Общий вид диаграммы приведен на рис.29. Для рассмотрения путей кристаллизации составов трехкомпонентной системы на пограничных кривых стрелками отмечается направление понижения температуры.

Правило 1:

Температура всегда понижается от точки пересечения пограничной кривой (или ее продолжения) с соединительной линией (или ее продолжения), соединяющей точки составов фаз, поля кристаллизации которых разделяет данная пограничная кривая. На пограничной кривой в точке ее пересечения с соединительной линией будет находиться температурный максимум.

Правило 1 иллюстрируется рис.30. Согласно этому правилу направление понижения температуры на пограничных кривых диаграммы (рис.29) будет определяться следующим образом. На кривой Е₁ – Е температура понижается от точки Е₁ к точке Е, так как точка Е₁ – точка пересечения соединительной линии АВ (совпадающая в данном случае со стороной проекционной диаграммы) и пограничной кривой Е₁ – Е, то есть точка Е₁ является точкой температурного максимума на кривой Е₁

– Е.

Рис.29. Диаграмма состояния трехкомпонентной системы с точкой тройной эвтектики

Правило 2:

Температура начала кристаллизации расплава или конца плавления твердой фазы соответствует температуре той изотермы диаграммы, на которую проецируется точка данного состава.

Например, температура начала кристаллизации компонента А исходного состава m (рис.29) соответствует температуре t₁.

При рассмотрении пути кристаллизации любого состава необходимо знать состав кристаллических фаз кристаллизующихся в каждый момент времени.

Правило 3:

При кристаллизации расплава первично выпадающей фазой будет тa, в поле первичной кристаллизации которой находится точка исходного состава. Если точка исходного состава принадлежит пограничной кривой, то первичными фазами будут тe, поля первичной кристаллизации которых разделяет данная пограничная кривая.

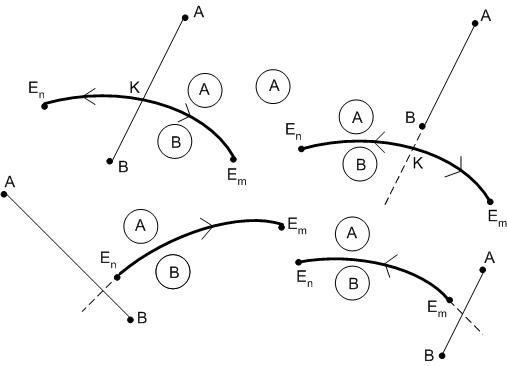
Рис.30. Направления понижения температуры на пограничных кривых

Прежде чем рассматривать пути кристаллизации составов системы, необходимо запомнить, что изменение состава расплава при кристаллизации происходит по линиям, проходящим через поля первичной кристаллизации или по пограничным кривым, а составы твердых фаз определяются на соединительных прямых.

Рассмотрим путь кристаллизации состава m (рис.29).

Выше температуры t₁ в равновесии будет находиться расплав состава точки m. При понижении температуры в момент пересечения поверхности ликвидуса (температура t₁) расплав становится пересыщенным по отношению к кристаллам компонента А. Начинается его кристаллизация (правило 3). При дальнейшем понижении температуры состав твердой фазы будет неизменен, состав же расплава будет изменяться по правилу 4.

Правило 4:

При кристаллизации из расплава одной твердой фазы состав жидкой фазы изменяется по продолжению прямой, проходящей в поле кристаллизации этой фазы и проведенной через точку состава первично выпадающей фазы и точку исходного состава в сторону понижения температуры.

После начала кристаллизации компонента А состав расплава будет изменяться по отрезку mM прямой АМ в сторону точки М. Как только состав расплава дойдет до пограничной кривой Е₁ – Е расплав становится пересыщенным по отношению к двум твердым фазам: А и В.

Кристаллы этих фаз будут одновременно выпадать из расплава. В этот момент времени степень свободы системы будет равна единице. Независимым термодинамическим параметром будет температура, а состав расплава будет изменяться при дальнейшем понижении температуры строго по пограничной кривой, то есть от точки М по кривой Е₁ – Е в сторону точки Е. При достижении температуры точки тройной эвтектики te начинается кристаллизация компонента С, так как в этом случае расплав становится пересыщенным по отношению сразу к трем компонентам. Нонвариантное состоянии, характерное для этого случая, заканчивается полной кристаллизацией расплава и дальнейшее возможное охлаждение системы приводит к охлаждению трех кристаллических фаз: А, В, С. Таким образом, путь кристаллизации исходного состава м: м→М→Е. Изменение фазового равновесия при нагревании будет обратным, нежели при охлаждении.

5.10 Правило рычага в трехкомпонентной системе

Для трехкомпонентной системы с помощью правила рычага можно решать следующие задачи:

1. определение количественного соотношения жидкой и твердой фаз при наличии одной твердой фазы;

2. определение количественного соотношения жидкой и твердой фаз при наличии двух кристаллических фаз с одновременным определением количественного соотношения кристаллических фаз в составе твердой фазы;

3. определение соотношения двух одновременно кристаллизующихся в данный момент времени фаз.

Рассмотрим работу правила рычага на примере диаграммы по рис.31.

Задача: определить фазовое равновесие исходного состава системы при температуре t₂.

К этой температуре в результате кристаллизации в системе в равновесии будут находиться две фазы: кристаллы А и расплав состава Lк. Для определения состава расплава следует провести прямые через точку К, параллельные сторонам треугольника.

Количественное соотношение равновесных фаз согласно правилу рычага будет определяться следующим образом. За 100% системы принимаем отрезок, ограниченный точками составов равновесных фаз, то есть точкой К (состав расплава) и точкой А (состав кристаллов А). Отношение ²расплав / кристаллы² будет обратно пропорциональным отрезкам прямой от точки исходного состава М до точек составов

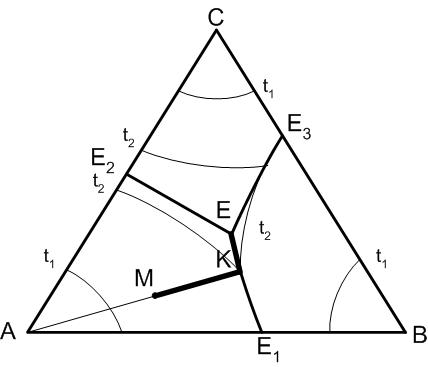равновесных фаз, то есть АМ: МК.

Рис.31. Правило рычага в трехкомпонентной системе

5.13. Диаграмма состояния трехкомпонентной системы с двойным химическим соединением, плавящимся конгруентно.

Признаком химического соединения, плавящегося конгруентно, является следующее:

Правило 5:

Химическое соединение плавится без разложения, если точка его состава принадлежит полю его первичной кристаллизации.

Соединительная прямая В – АС (компонент В и химическое соединение АС имеют сменные поля первичной кристаллизации) делит систему на два элементарных треугольника А – В – АС и В – АС – С, каждый из которых имеет точку тройной эвтектики. Для определения путей кристаллизации необходимо знать точку окончания кристаллизации исходных составов системы.

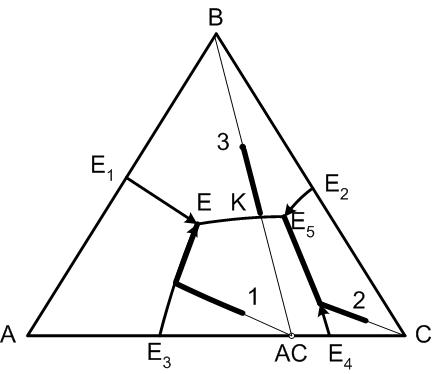Рис.32. Диаграмма трехкомпонентной системы с двойным химическим соединением, плавящимся конгруентно

Правило 6:

Окончание кристаллизации произвольного состава системы произойдет в точке, где пересекаются поля первичной кристаллизации фаз, находящихся в вершинах элементарного треугольника, которому принадлежит точка исходного состава.

Из этого правила следует, что все составы, находящиеся в элементарном треугольнике А – В – АС закончат свою кристаллизацию в точке Е, а конечными продуктами кристаллизации будут соответственно кристаллы компонентов А и В и кристаллы химического соединения АС. Если исходный состав (точка 3 на диаграмме) расположен на соединительной прямой В – АС, то этот случай рассматривается как диаграмма двухкомпонентной системы В – АС, для которой точка К является точкой двойной эвтектики и именно там окончится кристаллизация указанного состава.

5.14. Диаграмма состояния трехкомпонентной системы с двойным химическим соединением, плавящимся инконгруентно

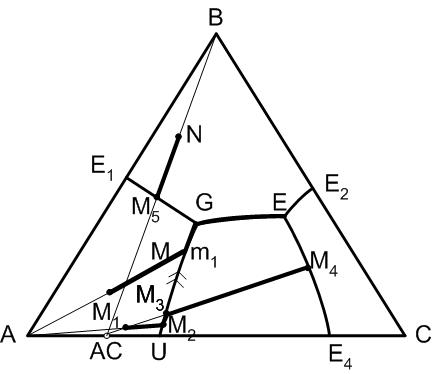Рис.33. Диаграмма трехкомпонентной системы с двойным химическим соединением, плавящимся инконгруентно

Признаком химического соединения, плавящегося инконгруентно, является следующее.

Правило 7:

Двойное химическое соединение в трехкомпонентной системе плавится с разложением, если точка состава этого соединения не принадлежит полю его первичной кристаллизации, а последнее примыкает к стороне проекционной диаграммы, на которой находится состав химического соединения.

При плавлении с разложением химическое соединение будет выделять расплав, состав которого определяется проекцией точки перитектики двухкомпонентной системы на сторону проекционной диаграммы, то есть состава U и кристаллы (в нашем случае компонента А).

Инконгруентные кривые в отличие от конгруентных являются кривыми химических реакций взаимодействия ранее выпавших кристаллов с расплавом. Для определения характера пограничной кривой существует следующее правило.

Дата добавления: 2014-01-04