
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Термодинамический вывод выражения для константы равновесия
|
|
|
|
Теперь рассмотрим более строгий термодинамический вывод выражения для константы равновесия. Для этого необходимо ввести понятие химический потенциал. Очевидно, что величина свободной энергии системы будет зависеть как от внешних условий, так и от природы и количества веществ, составляющих систему. В случае если количества веществ изменяются в ходе процесса, изобарно-изотермический потенциал является функцией не только температуры и давления, но и количеств веществ:
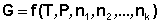 (10)
(10)
Для изохорно-изотермического потенциала имеем:
 (11)
(11)
При введении в некоторую систему бесконечно малого количество dni молей i-го компонента произойдёт изменение термодинамического потенциала системы на величину 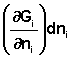 . При этом полный дифференциал G следует записать в следующем виде:
. При этом полный дифференциал G следует записать в следующем виде:
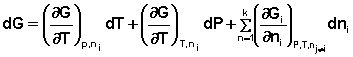 (12)
(12)
Аналогичным образом для полного дифференциала F получаем:
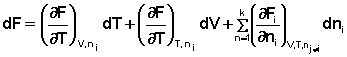 (13)
(13)
Частная производная термодинамического потенциала по числу молей компонента i-го компонента при постоянных количествах остальных компонентов есть химический потенциал μi данного компонента в системе:
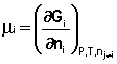 (14)
(14) 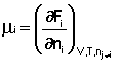 (15)
(15)
Иначе говоря, химический потенциал i-го компонента равен приращению свободной энергии системы при добавлении одного моля данного компонента к большому объёму системы при постоянных температуре и давлении (объёме). Понятие "большой объём системы" означает, что состав системы практически не изменяется после добавления одного моля компонента. Химический потенциал чистого вещества равен свободной энергии одного моля этого вещества.
Учитывая вышесказанное, уравнения (12-13) можно переписать в виде:
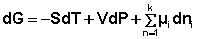 (16)
(16)
 (17)
(17)
При постоянстве температуры и давления (температуры и объёма) два первых слагаемых в уравнениях (16-17) обратятся в нуль. При этом получаем:
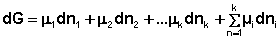 (18)
(18)
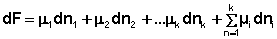 (19)
(19)
Поскольку условием равновесия является минимум свободной энергии системы (dG = 0, dF = 0), для состояния равновесия можно записать:
 (20)
(20)
Для вывода соотношения между парциальными давлениями либо концентрациями компонентов в равновесной смеси воспользуемся данным общим условием равновесия через химические потенциалы. Получим выражение для изменения свободной энергии при протекании в системе химической реакции:
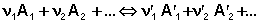
В закрытой системе изменение числа молей одного компонента сопровождается изменением числа молей остальных компонентов, пропорциональным стехиометрическим коэффициентам, взятым с соответствующим знаком ("–" для исходных веществ, "+" для продуктов реакции); т.е., для приведенной выше химической реакции имеет место соотношение:
 (21)
(21)
Здесь χ – т.н. химическая переменная, характеризующая только данную химическую реакцию. Поскольку dni = νidχ, для полного дифференциала G можно записать следующее выражение:
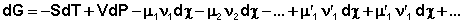 (22)
(22)
Отсюда получаем:
 (23)
(23)
Для системы, находящейся в состоянии равновесия получаем
 (24)
(24)
Выражение (24) носит название уравнения Гиббса – Дюгема. Для получения изотермы химической реакции нам следует выразить химический потенциал компонента через его парциальное давление или концентрацию. Если химическая реакция проводится при постоянной температуре, то выражение
 (25)
(25)
для полного дифференциала свободной энергии Гельмгольца преобразуется к виду dF = – PdV. Для одного моля идеального газа получаем:
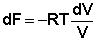 (26)
(26)
Отсюда получаем
 (27)
(27)
Здесь g(T) – постоянная интегрирования, представляющая собой некоторую функцию от температуры. Поскольку для одного моля идеального газа величина, обратная объёму, есть молярная концентрация, данное выражение преобразуется к виду:
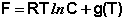 (28)
(28)
Как было показано ранее, для одного моля чистого вещества μ = F. Получаем:
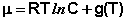 (29)
(29)
Для каждого из нескольких веществ в смеси можно записать
 (30)
(30)
Для стандартных условий (Сi = 1 моль/л) gi(T) = μ°i (стандартный химический потенциал). Окончательно получаем уравнение, связывающее химический потенциал компонента с его концентрацией:
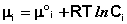 (31)
(31)
Аналогичным образом можно получить
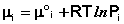 (32)
(32)
Подставив зависимость химического потенциала от парциального давления в уравнение (26), для состояния равновесия получаем:
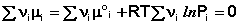 (33)
(33)
Для системы, находящейся в изохорно-изотермических условиях, аналогично получаем
 (34)
(34)
В уравнениях (33-34) Pi и Ci – равновесные парциальные давления и концентрации соответственно. Поскольку Σνiμ°i = const, получаем:
 (35)
(35)
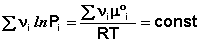 (36)
(36)
Для обсуждаемой химической реакции
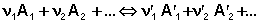
выражения (35) и (36) можно преобразовать к виду
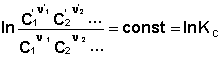 (37)
(37)
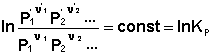 (38)
(38)
Потенцируя данные выражения, получаем, что в состоянии равновесия произведение концентраций либо парциальных давлений реагентов, взятых в степенях, равных стехиометрическим коэффициентам, при постоянной температуре есть некоторая постоянная величина – константа равновесия.
Изотерма химической реакции (изотерма Вант-Гоффа)
При самопроизвольном протекании химической реакции изменение свободной энергии системы отлично от нуля (ΔG < 0, ΔF < 0). Т.о., для самопроизвольного процесса можно записать:
 (39)
(39)
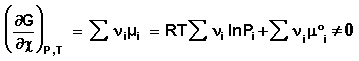 (40)
(40)
При протекании реакции в большом количестве реакционной смеси, таком, что при превращении ni молей каждого из компонентов концентрации реагентов Сi практически не изменяются, частную производную свободной энергии Гельмгольца по химической переменной можно заменить равной ей величиной отношения ΔF к Δχ, т.е. принять, что

Положив Δχ = 1, получаем
 (41)
(41)
Поскольку, как следует из (35,37), 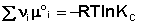 , окончательно получаем уравнение, называемое изотермой химической реакции (изотермой Вант-Гоффа):
, окончательно получаем уравнение, называемое изотермой химической реакции (изотермой Вант-Гоффа):
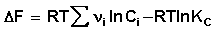 (42)
(42)
 (43)
(43)
Для изобарно-изотермического процесса аналогичным образом можно получить:
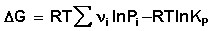 (44)
(44)
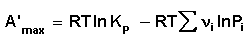 (45)
(45)
Уравнение изотермы Вант-Гоффа позволяет рассчитать максимальную работу химической реакции и тем самым определить возможность её самопроизвольного протекания в каких-либо конкретных условиях (при температуре Т и концентрациях реагентов Ci или парциальных давлениях Pi).
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1740; Нарушение авторских прав?; Мы поможем в написании вашей работы!