Условиях инвестирования

Расчет будущей стоимости вклада при различных

(усл. ден. ед.)

N9 варианта	Настоящая стоимость вклада	Ставка процента	Будущая стоимость вклада в конце
1-го периода	2-го периода	3-го периода	4-го периода
		100	130 145 200	169 –	186 – –	229 – – –

Сравнение вариантов показывает, что наиболее эф­фективным является 1-й вариант (выплата дохода в раз­мере 23% один раз в квартал).

Используемые в процессе оценки стоимости денег множители

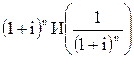называются соответственно множителем нара-

щения и множителем дисконтирования суммы сложных процентов. Они положены в основу специальных таблиц финансовых вычислений, с помощью которых при заданных размерах ставки процента и количе­ства платежных интервалов можно легко вычислить настоящую или будущую стоимость денежных средств по сложным процентам.

III. Методический инструментарий оценки стоимости денег при аннуитете связан с использованием наиболее сложных алгорит­мов и определением метода начисления процента — предваритель­ным (пренумерандо) или последующим (постнумерандо).

1. При расчете будущей стоимости аннуитета на условиях предварительных платежей (пренумерандо) используется следую­щая формула:

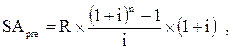
где 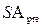— будущая стоимость аннуитета, осуществляемого на усло­виях предварительных платежей (пренумерандо);

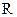— член аннуитета, характеризующий размер отдельного

платежа;

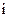— используемая процентная ставка, выраженная десятич­ной дробью;

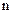— количество интервалов, по которым осуществляется каж­дый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), при следующих данных: период платежей по аннуитету предусмотрен В количестве 5 лет;

интервал платежей по аннуитету составляет один год (пла­тежи Вносятся В начале года);

сумма каждого отдельного платежа (члена аннуитета) со­ставляет 1000 усл. ден. ед.;

используемая для наращения стоимости процентная став­ка составляет 10% в год (0,1).

Подставляя эти значения В приведенную формулу, по­лучим :

будущая стоимость аннуитета, осуществляемого на усло­виях предварительных платежей (пренумерандо), равна:

усл. ден. единиц.

2. При расчете будущей стоимости аннуитета, осуще­ствляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:

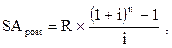
где 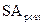— будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);

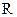— член аннуитета, характеризующий размер отдельного

платежа;

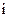— используемая процентная ставка, выраженная десятич­ной дробью;

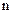— количество интервалов, по которым осуществляется каж­дый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях последующих пла­тежей (постнумерандо), по данным, изложенным В преды­дущем примере (при условии Взноса платежей В конце года).

Подставляя эти данные в приведенную формулу, по­лучим:

будущая стоимость аннуитета, осуществляемого на усло­виях последующих платежей (постнумерандо), равна:

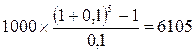усл. ден. единиц.

Сопоставление результатов расчета по двум приме­рам показывает, что будущая стоимость аннуитета, осу­ществляемого на условиях предварительных платежей, су­щественно превышает будущую стоимость аннуитета, осуществляемого на условиях последующих платежей, т. е. В первом случае плательщику обеспечена гораздо большая сумма дохода.

3. При расчете настоящей стоимости аннуитета, осуще­ствляемого на условиях предварительных платежей (пренумеран-до), используется следующая формула:

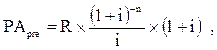
где 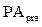— настоящая стоимость аннуитета, осуществляемого на

условиях предварительных платежей (пренумерандо);

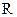— член аннуитета, характеризующий размер отдельного

платежа;

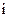— используемая процентная (дисконтная) ставка, выра­женная десятичной дробью;

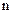— количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде вре­мени.

Пример: Необходимо рассчитать настоящую стои­мость аннуитета, осуществляемого на условиях предвари­тельных платежей (пренумерандо), при следующих данных:

период платежей по аннуитету предусмотрен в количестве 5 лет;

интервал платежей по аннуитету составляет один год (при внесении платежей 8 начале года);

сумма каждого отдельного платежа (члена аннуитета) со­ставляет 1000 усл. ден. ед.;

используемая для дисконтирования стоимости ставка про­цента (дисконтная ставка) составляет 10% в год (0,1).

Подставляя эти значения в приведенную формулу, по­лучим:

настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), равна: 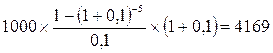усл. ден. единиц.

4. При расчете настоящей стоимости аннуитета, осуще­ствляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:

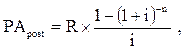
где 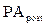— настоящая стоимость аннуитета, осуществляемого на

условиях последующих платежей (постнумерандо);

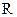— член аннуитета, характеризующий размер отдельного

платежа;

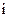—используемая процентная (дисконтная) ставка, выра­женная десятичной дробью;

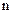— количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде вре­мени.

Пример: Необходимо рассчитать настоящую сто­имость аннуитета, осуществляемого на условиях последу­ющих платежей (постнумерандо), по данным, изложенным в предыдущем примере (при условии взноса платежей в конце года).

Подставляя эти данные в приведенную формулу, по­лучим:

настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), равна:

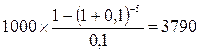усл. ден. единиц.

Сопоставление результатов расчета по двум послед­ним примерам показывает, что настоящая стоимость ан­нуитета, осуществляемого на условиях предварительных платежей, существенно превышает настоящую стоимость аннуитета, осуществляемого на условиях последующих пла­тежей, т.е. в первом случае в процессе дисконтирования плательщику гарантирована гораздо большая сумма дохо­да в настоящей стоимости.

5. При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется следующая формула:

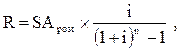
где 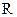— размер отдельного платежа по аннуитету (член аннуите­та при предопределенной будущей его стоимости);

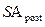— будущая стоимость аннуитета (осуществляемого на усло­виях последующих платежей);

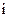— используемая процентная ставка, выраженная десятич­ной дробью;

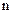— количество интервалов, по которым намечается осуще­ствлять каждый платеж, в обусловленном периоде вре­мени.

6. При расчете размера отдельного платежа при заданной текущей стоимости аннуитета используется такая формула:

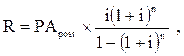
где 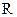— размер отдельного платежа по аннуитету (член аннуите­та при известной текущей его стоимости);

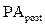— настоящая стоимость аннуитета (осуществляемого на

условиях последующих платежей);;

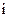— используемая процентная ставка, выраженная десятич­ной дробью;

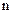— количество интервалов, по которым намечается осуще­ствлять каждый платеж, в обусловленном периоде вре­мени.

В процессе расчета аннуитета возможно использование упро­щенных формул, основу которых составляет только член аннуитета (размер отдельного платежа) и соответствующий стандартный мно­житель (коэффициент) его наращения или дисконтирования.

В этом случае формула для определения будущей стоимости аннуитета (осуществляемого на условиях последующих платежей), имеет вид:

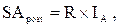
где 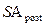— будущая стоимость аннуитета (осуществляемого на

условиях последующих платежей);

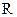— член аннуитета, характеризующий размер отдельного

платежа;

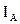— множитель наращения стоимости аннуитета, определя­емый по специальным таблицам, с учетом принятой процентной ставки и количества интервалов в перио­де платежей.

Соответственно, формула для определения настоящей стоимо­сти аннуитета имеет вид:

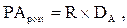
где 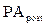— настоящая стоимость аннуитета (осуществляемого на

условиях последующих платежей);

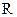— член аннуитета, характеризующий размер отдельного

платежа;

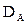— дисконтный множитель аннуитета, определяемый по специальным таблицам, с учетом принятой процентной (дисконтной) ставки и количества интервалов в пери­оде платежей.

Использование стандартных множителей (коэффициентов) на­ращения и дисконтирования стоимости существенно ускоряет и об­легчает процесс оценки стоимости денег во времени.

Дата добавления: 2014-01-04