Методи дослідження наносистем

Теорія до задач

Методи дослідження нанооб’єктів направлені, перш за все, на визначення розмірних і структурних характеристик наноматеріалів, встановлення впливу розмірних ефектів на їх властивості.

Відомо, що частинки, розмір яких знаходиться в нанодіапазоні (1 – 100 нм), не можна спостерігати за допомогою оптичної мікроскопії, оскільки цьому перешкоджає явище дифракції випромінювання на частинках, розмір яких менший за довжину хвилі. Явище дифракції полягає в тому, що світлові промені огинають наночастинки і змінюють свій напрямок, розсіюючись у всі сторони.

Інтенсивність світла, розсіяного в результаті дифракції на наночастинках, залежить від кількості та розмірів частинок, а також від довжини хвилі падаючого світла. Ця залежність виражається рівнянням Релея, яке для сферичних частинок, що не поглинають світло, має вигляд:

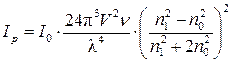, (9.1)

де І ₀ і І _р – інтенсивності падаючого і розсіяного світла; V – об’єм частинки; λ – довжина хвилі падаючого світла; ν – частинкова концентрація (число частинок в 1 м³ золю); n ₁ і n ₀ – показники заломлення дисперсної фази і дисперсійного середовища.

У рівняння (9.1) входить частинкова концентрація дисперсної фази ν, яка визначається числом частинок в одиниці об’єму. Частинкова концентрація пов’язана з масовою концентрацією дисперсної фази співвідношенням:

с = V ∙ρ∙ν, (9.2)

де с – масова концентрація (маса частинок дисперсної фази в 1 м³ золю); V – об’єм частинки; ν – частикова концентрація (число частинок в 1 м³ золю), ρ – густина дисперсної фази.

З врахуванням (9.2), рівняння Релея набуде вигляду:

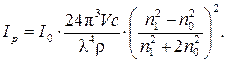(9.3)

Це рівняння використовується для визначення концентрації наночастинок та їх розміру.

Із рівняння Релея слідує, що інтенсивність розсіяного світла обернено пропорційна довжині хвилі падаючого світла: І _р ≈ 1/λ⁴. Відповідно, чим коротша довжина хвилі падаючого світла, тим більше розсіювання.

На вимірюванні інтенсивності світла, що пройшло через шар наносистеми певної товщини, базується турбідиметричний метод аналізу дисперсних систем. Інтенсивність світлового потоку, що проходить через систему послаблюється пропорційно зростанню інтенсивності світлорозсіяння. Якщо умовно прийняти розсіяне світло за поглинуте, то справедливим буде співвідношення аналогічне закону Бугера-Ламберта-Бера:

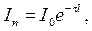(9.4)

де τ − коефіцієнт пропорційності, який характеризує здатність системи розсіювати світло (мутність системи); l − товщина шару. Мутність τ виражається відношенням інтенсивностей розсіяного і падаючого світла, віднесеної до одиниці довжини зразку. Застосувавши рівняння Релея і скориставшись вимірюваннями оптичної густини системи (τ∙ l = 2,3 D), можна встановити розміри частинок, проводячи порівняння зі стандартним золем.

Мутність досліджуваного і стандартного розчинів оцінюють в нефелометрі по висоті стовпчиків рідин h, що забезпечує рівну освітленість полів в окулярі. В цьому випадку при постійному розмірі частинок можна оцінити масову концентрацію частинок золю:

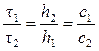, (9.5)

а при постійній концентрації частинок дисперсної фази - їх розмір:

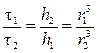. (9.6)

Явище розсіювання світла використовується для визначення розміру частинок за допомогою ультрамікроскопу. Для цього підраховують середнє число частинок n в певному об’ємі V сильно розбавленого золю (беруть середнє число із сотні підрахунків).

Маса частинок дисперсної фази m у видимому об’ємі V рівна:

m = c∙V, (9.7)

де m – маса частинок дисперсної фази, кг; с – масова концентрація (маса частинок дисперсної фази в 1 м³ золю), кг/м³, V – видимий в ультрамікроскоп об’єм золю, м³.

Маса однієї частинки m ₀, буде рівна:

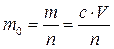, (9.8)

де n – число частинок дисперсної фази, видимих в ультрамікроскоп.

Тоді об’єм однієї частинки дисперсної фази рівний:

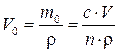, (9.9)

де ρ – густина частинок дисперсної фази, кг/м³.

Для частинок сферичної форми 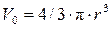, для частинок кубічної форми .

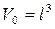Тоді середній радіус однієї частинки сферичної форми буде рівний:

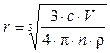(9.10)

Довжина ребра частинки кубічної форми буде рівна:

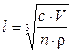(9.11)

Поглинання світла залежить від індивідуальних фізичних і хімічних властивостей речовин і є вибірковим, тобто кожна речовина поглинає світло певних довжин хвиль. З цим пов’язане забарвлення тіл.

В розчинах з прозорим розчинником світло поглинається тільки розчиненою речовиною. Для них справедливе рівняння Бугера-Ламберта-Бера:

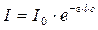, (9.12)

де І ₀ і І – інтенсивності падаючого світла і світла, що пройшло крізь розчин; l – товщина поглинаючого шару; ε – коефіцієнт світлопогли­нання, c – концентрація дисперсної фази.

Логарифм відношення інтенсивності падаючого світла до інтенсивності світла, що пройшло крізь розчин називається оптичною густиною (А):

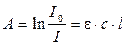. (9.13)

Це дозволяє оцінити концентрацію дисперсної фази, порівнюючи оптичні густини досліджуваного і стандартного розчину з відомою концентрацією частинок. При рівній товщині шару справедливим є відношення 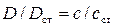, звідки:

c = c _ст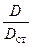. (9.14)

Перевірка можливості застосування закону Бугера-Ламберта-Бера:

3) аналітична – розраховані значення коефіцієнту поглинання ε для різних концентрацій одного і того ж золю повинні мати близькі чисельні значення.

4) графічна – залежність оптичної густини від концентрації повинна бути лінійною і виходити із початку координат. Якщо поглинання світла дисперсною системою підпорядковується закону Бугера-Ламберта-Бера, то вимірявши оптичну густину золю, можна знайти концентрацію дисперсної фази:

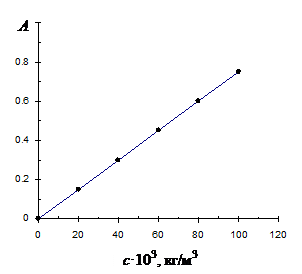
Рис. 9.1. Залежність оптичної густини від концентрації, що підпорядковується закону Бугера-Ламберта-Бера

Для дисперсійного аналізу наносистем більш придатна електронна мікроскопія. В ній замість світлових променів використовують потік електронів, зменшуючи довжину хвилі і тим самим збільшуючи роздільчу здатність мікроскопу. При різниці потенціалів 50 кВ, що використовується для емісії електронів в існуючих електронних мікроскопах, теоретична роздільча здатність складає 0,5 - 1,0 нм. На практиці використання електронних мікроскопів різноманітних конструкцій дозволяє досліджувати об’єкти розміром до 5 - 10 нм.

На практиці найбільш широко використовується просвічуюча електронна мікроскопія, при якій потік електронів частково поглина­ється просвічуючим об’єктом, а отримане зображення проектується на реєструючий прилад. Електронна мікроскопія високого розрізнення дозволяє визначати не тільки розміри частинок, але і деталі їх будови.

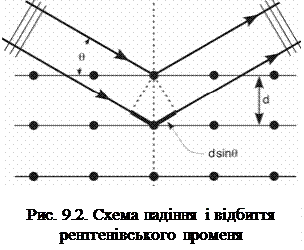Для визначення структури кристалічних наноматеріалів ши­роко використовується рентгено­структурний аналіз. В основі даного методу лежить явище дифракції рентге­нівських проме­нів на трьохвимір­ній кристалічній гратці (рис. 9.2). Кристалічна решітка в заданому напрямку може розгля­датися як серія паралельних площин, які знаходяться на відстані одна від одної d. Коли монохромати­зований рентгенівський промінь з довжиною хвилі λ падає на систему кристалічних площин під кутом θ, дифракція виникає тільки тоді, якщо шляхи, які проходять промені, відбиті від різних кристалічних площин відрізняються на ціле число довжин хвиль. Це явище описується законом Брегга: nλ = 2d∙sinθ.

При зміні кута θ, умова закону Брегга задовольняється почергово для різних систем площин в полікристалічному матеріалі, в результаті чого на дифрактограмі досліджуваної речовини послідовно, зі зміною кута, з’являються рентгенівські рефлекси – піки (лінії дифрактограми) з явними максимумами (рис. 9.3). Координати та висота піків характери­зують досліджувану речовину.

Рис. 9.3. Типова рентгенівська дифрактограма зразку, що містить наночастинки нікелю

Типова дифрактограма полікристалу являє собою серію піків на плавній лінії фону. Кожний пік є відбиттям n -го порядку від серії площин (hkl) з міжплощинною відстанню d_hkl. (hkl) – це кристалографічні індекси площини (індекси Міллера), які завжди цілі числа (наприклад, 111, 200, 220, 311, 222).

Кожна кристалічна фаза має індивідуальну дифракційну картину, яка визначається положенням ліній та їх інтенсивністю. Дифрактограма суміші декількох фаз є результатом накладання дифрактограм кожної із них. Тому визначення одної фази чи суміші декількох фаз може бути проведено шляхом порівняння дифрактограм відомих сполук і досліджуваної речовини, тобто рентгенодифрактометричне визначення сполук зводиться до співставлення даних експерименту положення піків та їх інтенсивностей з такими ж із довідника.

Рентгенографічні методи визначення дисперсності базуються на аналізі ширини дифракційних ліній. Характерною особливістю рент­генівських дифрактограм нано­роз­мірних систем є розширення дифракційних ліній порівняно з об’ємним матеріалом. Ширина дифракційного максимуму (b) визначається на половині його висоти (рис. 9.4). Причому, ширина кожної експериментальної лінії b складається із двох частин: інструментальної ширини b₀ (ширина лінії еталону), яка залежить від геометрії зйомки, розходження пучка, розміру фокусу трубки і т.д., і фізичного розширення b_зразок, що визначається факторами недосконалості струк­тури (дисперсністю, мікроспотво­реннями, дефектами упаковки і т.д.). Тому для того, щоб одержати правильне значення β, необхідно порівнювати лінії досліджуваного зразку з лініями еталону, який являє собою добре кристалізо­ваний порошок того ж матеріалу, що має зерна з розміром >300 нм. Для внесення відповідної поправ­ки зазвичай користуються форму­лою Уоррена (9.15). Якщо β_зразок – виміряна напівширина лінії, а β₀ – напівширина дифракційної лінії стандарту, то виправленим зна­ченням буде:

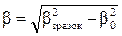, (9.15)

Знайдене таким чином фізичне уширення b може бути використане для визначення розмірів кристалітів:

(9.16),

де D – середній діаметр частинок (нм), λ – довжина хвилі застосованого рентгенівського випромінювання (нм), cos(θ) – косинус кута, при якому спостерігається максимум, β – напівширина дифракційної лінії досліджуваного зразку (рад); 1рад = (1º∙π)/180º.

Формула (9.16) була виведена в 1918 р. Шеррером і незалежно в 1923 р. Селяковим і називається формулою Шеррера-Селякова.

Міжплощинні відстані d_hkl в кристалі можна визначити за формулою Вульфа-Брегга:

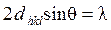, (9.17)

де sin(θ) – синус кута, при якому спостерігається максимум, λ – довжина хвилі застосованого рентгенівського випромінювання.

Сталу ґратки а₀ визначають за формулою:

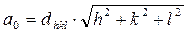,(9.18)

де h, k, l – індекси Міллера атомної площини в кристалі.

Значний прорив в дослідженні наностану речовини пов’язаний зі створенням скануючих зондів.

Скануюча зондова мікроскопія – сукупність методів визначення локальних механічних, електричних, магнітних та інших властивостей поверхні за допомогою різних мікрозондів. Використовуючи ці методи, одержують тривимірне зображення поверхні матеріалів з роздільчою здатністю в декілька часток нанометра. Принцип дії скануючого тунельного мікроскопу базується на проходженні електроном потенціального бар’єру, утвореного розривом електричного ланцюга – невеликим проміжком між зондуючим мікровістрям і поверхнею зразка. Вістря наближають до поверхні провідника до появи тунельного струму. Для отримання зображення поверхні вістря переміщають, підтримуючи сталу величину струму. Скануюча тунельна мікроскопія застосовується для аналізу поверхні при умові електропровідності носія. За допомогою атомно-силового мікроскопу досліджуються будь-які матеріали. Його основою є над гостра голка – кантилевер. Підтримуючи постійною силу міжатомного притягання кантилевера і поверхні, можна побудувати атомний рельєф досліджуваного зразка. Атомно-силовий мікроскоп дозволяє виміряти локальні сили тертя, величину адгезії, пружні і в’язкі властивості поверхні з субнанометровою просторовою роздільчою здатністю.

Дата добавления: 2014-01-04