Процес розмноження і загибелі

Розглянемо типову схему неперервних Марківських ланцюгів - ”схему загибелі і розмноження”, у якій усі стани, крім крайніх, зв'язані прямим і зворотним зв'язком з кожним із двох сусідніх станів, а крайні S_1, Sn-тільки з одним сусіднім.

Знайдемо границю імовірності для такої системи.

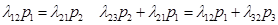
з огляду на вищезгадане, одержимо: 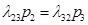аналогічно: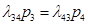

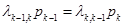,для k=2,...,n

у такий спосіб межа імовірності станів Р₁, Р₂,...., Р_n у схемі загибелі і розмноження задовольняє системі:

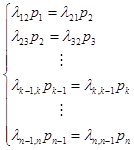(10)

і нормованій умові P₁+P₂+....+P_n (11.)

З рівнянь системи (10) виразимо всі P_k, k=2,n через p₁

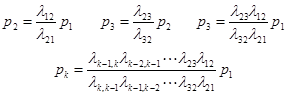
У чисельнику стоїть добуток всіх інтервалів λ_ij стрілок спрямованих вперед від початкової до вхідної в S_k, у знаменнику- усіх йдучих назад від S_k до S₀ .

При k=n, у чисельнику

Підставляючи (12) у (11) одержимо

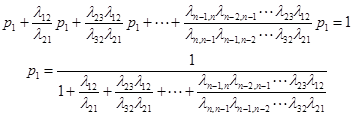
Це дає нам загальний вигляд границі імовірностей схеми розмноження і загибелі.

Приклад 3. Знайти граничні імовірності для системи:

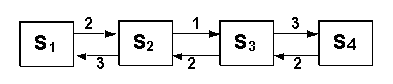
по (13) і (12):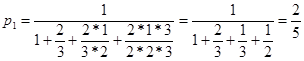

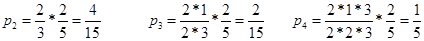
Приклад 4 Прилад складається з 3х вузлів, потік відмов - найпростіший, середнє час безвідмовної роботи будь-якого вузла t_б. Вузол, що відмовив, відразу починає ремонтуватися, середній час ремонту tр (потік відновлення найпростіший). Знайти середню міцність приладу, якщо при 3 працюючих вузлах вона=100%, при 2х=50%, а при 1 прилад не працює.

Рішення.

Для потоку відмов λ=1/t_б, відновлень - 1/t_p.

S₀ - працюють 3 вузли, на кожнім діючий потік λ=1/t_б виходить, потік відмовлень системи в 3 рази інтенсивніше λ₀₁=3/t_б.

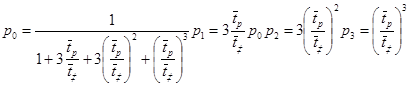
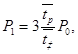
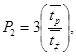
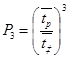
Нехай 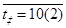, t_p=5*2, тоді p₀=8/27; p₁=12/27,p₂=6/27, p₃=1/27

Середня щільність у сталому режимі 100% p₀+50% p₁=(300/27+600/27)%=51.9%.

Дата добавления: 2014-01-04