Рудюк В.Л

Потік вектора напруженості електростатичного поля у вакуумі через довільну замкнену поверхню зсередини назовні дорівнює алгебраїчній сумі тих зарядів, які охоплюються поверхнею, поділеній на електричну сталу.

Алгебраїчна сума електричних зарядів тіл чи частинок, які утворюють електрично ізольовану систему, не змінюється за будь-яких процесів, що відбуваються в цій системі”, тобто у електрично ізольованій системі електричні заряди можуть виникати, або зникати лише парами (позитивний + негативний), причому так, що загальний заряд системи є незмінним у часі.

Розділ фізики, в якому вивчається взаємодія нерухомих електричних зарядів (електростатична взаємодія) називають електростатикою. Оскільки рух або спокій зарядів відносні і визначаються станом інерціальної системи відліку, то ті ж самі заряди в одних системах відліку, відносно яких вони нерухомі, проявляють електростатичну взаємодію, а в інших, відносно яких заряди рухаються, – електромагнітну взаємодію. Отже, чисто електростатична взаємодія зарядів є відносною і проявляється лише в тих системах відліку, відносно яких ці заряди нерухомі. Взаємодія нерухомих зарядів відбувається через електростатичне поле, джерелами якого і являються ці нерухомі заряди. Оскільки поле зарядів локалізоване в просторі, навколо них це поле в кожній точці простору характеризується рядом фізичних величин, то електростатичним часто називають поле, характеристики якого в кожній точці незмінні з часом.

Поняття електроємності. Конденсатори

Теорема Остроградського-Гауса

Робота сили електричного поля. Потенціал

Напруженість електричного поля. Принцип суперпозиції

Електричний заряд. Закон Кулона. Електричне поле

ü Електричний заряд. Закон Кулона. Електричне поле

Електричний заряд є внутрішньою характеристикою деяких елементарних частинок, яка проявляється у їхній взаємодії на відстані або під час дії на них зовнішніх електромагнітних полів. Електричний заряд являється джерелом і об’єктом дії електромагнітного поля.

Відомо, що в природі існують два типи електричного заряду: позитивні(додатні) та негативні(від’ємні), причому однотипні заряди відштовхуються один від одного, а заряди різних типів – взаємно притягуються.

Вважаємо відомим факт існування найменших, неподільних зарядів кожного типу – квантів заряду, або елементарних зарядів: 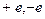. Елементарний електричний заряд за модулем дорівнює 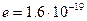Кл. (Кулон – одиниця виміру електричного заряду).

Кожен електричний заряд в природі складається з цілої кількості елементарних зарядів:

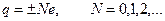
(1)

Передаватися від тіла до тіла електричний заряд також може лише квантами: у вигляді цілого числа елементарних зарядів. Квантовий характер електричного заряду є надзвичайно важливим в мікросвіті, де типова величина електричних зарядів дорівнює декільком квантам заряду (тобто ).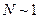

Однією з важливих властивостей елементарного заряду є інваріантність – незалежність його величини від стану інерціальних систем відліку, в яких визначається його числове значення, тобто числове значення заряду не залежить від швидкості.

Незважаючи на відносну самостійність, заряд не існує незалежно від носіїв заряду, тобто від матерії, поза простором і часом. Заряд – це одна із фундаментальних властивостей матерії. Носіями позитивних елементарних зарядів є такі мікрочастинки як протони, тоді як електрони мають рівний за модулем, але протилежний за знаком, від’ємний елементарний заряд.

Для макротіл звичайно 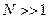, тому квантовий характер заряду не проявляється. В таких випадках вважають, що електричний заряд розподілений у провіднику неперервно і дискретною структурою заряду нехтують. Тому вводиться поняття об’ємної, поверхневої і лінійної густини неперервно розподілених зарядів.

Об’ємну густину заряду в даній точці простору визначають як границю відношення заряду 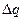, який міститься в об’ємі 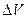, що оточує точку, до величини цього об’єму:

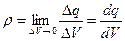
(2)

Аналогічно введемо поняття поверхневої густини заряду:

Поверхневу густину заряду в даній точці простору визначають як границю відношення заряду 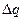, який містить малий елемент зарядженої поверхні площею 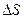, що оточує точку, до величини цієї площі:

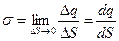
(3)

Та лінійної густини заряду

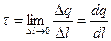
(4)

При цьому 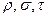вважають неперервними функціями координат.

Система тіл чи частинок за умови відсутності обміну електричними зарядами з навколишніми тілами називається електрично ізольованою системою. Для таких систем є справедливим закон збереження електричного заряду:

У 1785р. французький військовий інженер, член Паризької Академії наук Шарль Огюстен Кулон у своїх мемуарах описав встановлений ним експериментально (за допомогою крутильних терезів) закон взаємодії точкових електричних зарядів у вакуумі.

Точковим зарядом у фізиці називають протяжне заряджене тіло, розміри якого малі у порівнянні із відстанню до інших зарядів.

Із дослідом Кулона можна ознайомитися у [5-9]. Ми ж перейдемо до висновків, які зробив Кулон. По-перше, сила взаємодії двох точкових зарядів напрямлена уздовж лінії, яка з’єднує обидва заряди та обернено пропорційна квадрату відстані між зарядами:

~

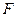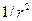
(5)

По-друге, сила взаємодії кульок залежить від величин цих зарядів.

~

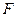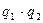
(6)

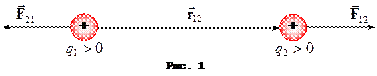Отже, закон Кулона у векторній формі для сили взаємодії двох точкових нерухомих зарядів у вакуумі має наступний вигляд:

=

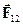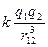
(7)

де 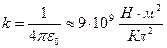- коефіцієнт пропорційності,

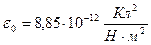– електрична стала,

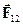- вектор сили, з якою заряд 1 діє на заряд 2,

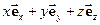=- радіус-вектор, напрямлений від заряду 1 до заряду 2.

Закон Кулона у вигляді (7) справедливий як для позитивних так і для негативних зарядів.

Виникає питання походження взаємодії нерухомих електричних зарядів. У фізиці мали місце дві протилежні за змістом концепції: далеко- та близькодії.

Згідно з першою концепцією дія від одного заряду до іншого передається миттєво без участі будь-якого матеріального носія цієї взаємодії і що при наявності тільки одного заряду ніяких змін у навколишньому просторі не відбувається.

Концепція близькодії передбачала, що взаємодія між нерухомими зарядами передається через електричне поле, яке оточує ці заряди, зі скінченою швидкістю від одних точок поля до інших.

Концепція далекодії не відповідала дійсності і була відкинута після відкриття та дослідження електромагнітного поля.

Отже, матеріальним носієм взаємодії нерухомих зарядів є електричне поле. Основною властивістю електричного поля є те, що на будь-який інший заряд у цьому полі діє сила. Але у фізиці також користуються поняттям електростатичного поля, джерелами якого є нерухомі заряди.

ü Напруженість електричного поля. Принцип суперпозиції

Однак є певна незручність: вона полягає у тому, що обидва заряди 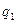та 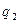оточені власними електричними полями. Ці два поля взаємодіють поміж собою і утворюють спільне поле (іншими словами суперпозицію полів) пари зарядів .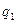

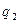Якщо нам хотілося б вивчити окремо, приміром, поле, створене зарядом 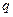, то це можливо лише при спостереженні його впливу на внесений в поле інший, так званий „пробний” заряд 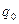. Проте цей пробний заряд (індикатор поля) власним електричним полем неминуче збурить (трансформує) поле заряду 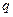, яке ми хотіли б вивчати осібно від поля заряду .

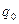Єдиний вихід з цієї проблеми полягає в тому, аби зробити „пробний” заряд набагато меншим від „утворюючого поле заряду”: 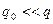. Сподіваючись, що „пробний заряд” 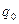практично не вплине своїм полем на електричне поле, яке він „тестує”.

Якщо враховувати лише модуль сили Кулона, то вираз (7) спрощується:

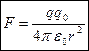
(7а)

Отже, на пробний заряд 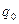діятиме сила 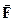(різна у різних точках поля), яка у відповідності до закону Кулона (7а) буде пропорційна пробному заряду 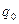. Але який би за величиною ми не брали пробний заряд, відношення сили, з якою електричне поле в даній точці простору діятиме на цей заряд, до величини цього пробного заряду, буде величина стала для даної точки простору:

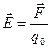
(8)

Ця величина є силовою характеристикою електричного поля і називається напруженість. Тобто, якщо електричне поле створене точковим зарядом 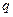, то напруженість поля згідно з законом Кулона:

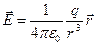
(8а)

де 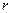- модуль відстані від заряду до досліджуваної точки поля, 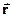- радіус-вектор, спрямований від заряду у дану точку поля. В СІ напруженість електричного поля вимірюється у ньютонах на кулон .

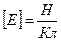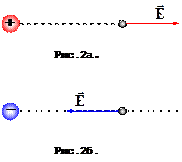
Поле точкового заряду є центральносиметричним. Напруженість поля точкового заряду спадає обернено пропорційно квадрату відстані від заряду. Так як електричний заряд є скаляром, а сила – векторна величина, то напруженість поля також є вектором. Напрям цього вектора визначає напрям сили, яка діє на пробний (позитивний одиничний точковий) заряд, розташований у досліджуваній точці поля (Рис.2а,б). Наприклад, якщо поле створене позитивним зарядом, то вектор напруженості спрямований уздовж радіус-вектора від заряду у зовнішній простір.

З (8) бачимо, що при відомій напруженості поля у деякій точці тим самим визначена сила, яка діє на електричний пробний заряд, поміщений у дану точку поля.

Для опису електричного поля необхідно задати вектор напруженості у кожній точці поля. Це можна зробити аналітично, якщо виразити залежність напруженості від координат у вигляді формул. Однак, таку залежність можна представити і графічно, за допомогою так званих силових ліній - ліній напруженості електричного поля.

Лініями напруженості електричного поля (або лініями вектора ) називають лінії, дотичні до яких спрямовані також як і вектор напруженості у даній точці поля.

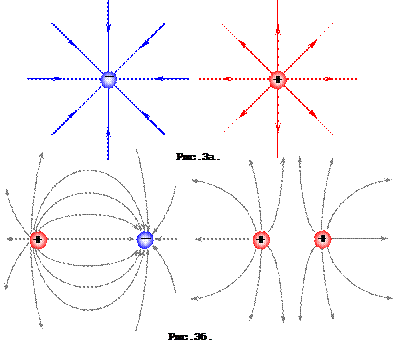Оскільки дотична, як і будь-яка пряма, має два взаємно протилежних напрямки, то напрямок лінії напруженості позначають стрілкою на кресленні. Для того, аби за допомогою ліній напруженості вказати не тільки напрямок а й модуль напруженості поля, умовилися на графіках поля проводити лінії напруженості із певною густиною так, щоб кількість ліній, які проходять через одиницю поверхні, перпендикулярної до них, дорівнювала (або була пропорційною) напруженості поля у даній точці простору.

Лінії напруженості ніде не перетинаються. Вони починаються на позитивно заряджених тілах, а закінчуються на негативно заряджених (Рис.3а), тобто на оточуючих тілах, на яких виникають індукційні заряди. Силові лінії поля двох точкових зарядів – криві (Рис.3б). У випадку заряджених тіл складної форми такі розрахунки можуть бути доволі складними.

Електричне поле, в якому величина і напрям напруженості однакові для будь-яких точок поля, називають однорідним. Силові лінії такого поля паралельні між собою і мають однаковий напрям.

Основним завданням електростатики є саме знаходження величини і напряму вектора напруженості 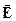в кожній точці поля за заданим розподілом у просторі та величиною зарядів.

Якщо відомо напруженості полів, створених окремо довільною системою точкових зарядів 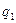, ,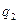..., , 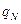то виникає питання, якою буде результуюча напруженість в довільно обраній точці поля? Дослід показує, що напруженість результуючого поля системи зарядів дорівнює векторній сумі напруженості полів цих зарядів окремо, тобто:

(9)

де індекс 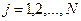нумерує дискретні заряди, кожен з яких є окремим незалежним від інших джерелом поля в точці спостереження. Співвідношення (9) виражає принцип суперпозиції електричних полів, тобто принцип незалежності дії електричних полів.

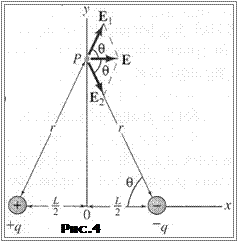Припустимо, що в точці спостереження електростатичні поля одночасно створюють два джерела: заряди та . Принцип суперпозиції полів стверджує, що в такому разі результуюча напруженість знаходиться як векторна сума напруженостей полів, створених окремими точковими джерелами (зарядами) незалежно один від одного (у випадку двох зарядів – за правилом паралелограма):

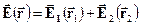
Зверніть увагу, що вектор напруженості 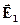спрямовано від заряду-джерела 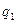, а вектор 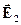, навпаки, до заряду-джерела .

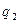У випадку, якщо джерело поля – електричний заряд – розподілений в просторі безперервно, а не у вигляді точкових зарядів, суму по зарядах в (9) слід замінити на векторний інтеграл по всім тим об’ємам в просторі, в яких густина заряду 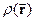відмінна від нуля. Припустимо, що елементарний заряд 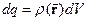створює в точці спостереження елементарне поле з напруженістю 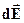, величина і напрям якого залежить від взаємного розташування точки спостереження та точки 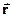, а також від величини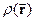. Принцип суперпозиції в такому випадку вимагає знайти результуюче поле як інтеграл, який враховує вплив всіх таких елементарних джерел:

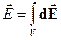
(9а)

Послідовно застосовуючи принцип суперпозиції можна знайти результуюче поле в точці спостереження при будь-якому розподілі джерел поля в просторі.

ü Робота сил електричного поля. Потенціал

Розглянемо пробний точковий електричний заряд 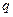в електричному полі заряду 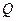із напруженістю 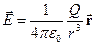, на який у цьому полі діє сила 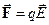. Ця сила є центральною, а поле центральних сил консервативне. Отже, при переміщенні заряду в полі ця сила виконуватиме роботу, причому величина роботи по переміщенню заряду 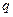в електростатичному полі залежить лише від його початкового та кінцевого положення і не залежатиме від траєкторії руху.

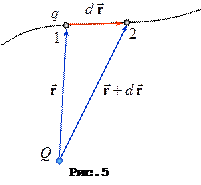
Розглянемо роботу з переміщення пробного заряду 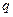в електростатичному полі заряду 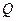з точки, яка виражається радіус-вектором 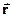у точку з (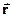+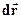). Оберемо вектор переміщення 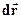таким чином, щоб він співпадав із силовою лінією електричного поля. З курсу механіки відомо, що робота дорівнює скалярному добутку сили, що діє на заряд, на його переміщення:

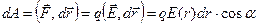
(10)

У даному випадку ситуація спрощується, оскільки косинус кута поміж векторами напруженості 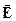(дотичного до силової лінії) та переміщення 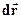дорівнює одиниці, то:

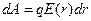
(11)

Якщо треба визначити роботу з переміщення заряду на довшому шляху (від певної точки 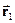до іншої точки 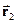, причому відстань поміж цими точками (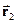-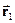) не є нескінченно малою, то роботу можна шукати як інтеграл:

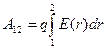
(12)

З врахуванням 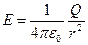маємо:

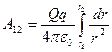
(13)

Результат інтегрування має наступний вигляд:

(13б)

Роботу сил консервативного поля можна представити як зменшення потенційної енергії:

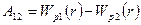
(14)

Звідси отримуємо вираз для потенційної енергії заряду 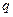у полі заряду :

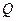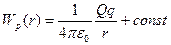
(15)

Значення константи у виразі потенційної енергії (15) обирають таким чином, аби при віддаленні заряду не нескінченність (при 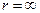) потенційна енергія оберталася в нуль, тоді:

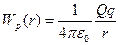
(15а)

Але ми користуємося саме пробним зарядом 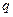, отже ми можемо досліджувати за допомогою нього поле заряду 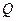у будь-якій точці простору.

Але відношення 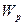до величини пробного заряду 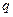не залежатиме від величини пробного заряду, тобто буде характеризувати лише поле джерела в даній точці простору:

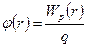
(16)

величина 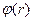називається потенціалом поля в даній точці і використовується, як і напруженість електричного поля 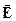, для опису електричних полів, а 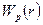- потенційна енергія електричного поля у точці з радіус-вектором .

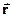Потенціал електричного поля вимірюється у 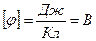(на честь італійського фізика Алессандро Вольти).

Потенціал електричного поля є скалярною характеристикою поля (на відміну від напруженості, яка є вектором). Він є енергетичною характеристикою поля, яку можна визначити як потенційну енергію одиниці заряду в певній точці поля. Отже, потенціал (надалі позначатиме його просто 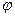) електричного поля точкового заряду 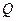у точці 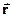дорівнюватиме:

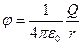
(17)

Вочевидь, що для системи зарядів справедливим є твердження, що робота, яку виконують сили поля, створеного системою точкових зарядів, над пробним зарядом 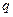буде дорівнювати алгебраїчної сумі робіт, виконуваних кожним окремим зарядом:

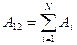
(18)

В такому випадку потенційна енергія пробного заряду в полі системи зарядів та потенціал матимуть вигляд:

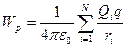
	(19)
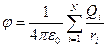
	(20)

Бачимо, що потенціали додаються алгебраїчно, на відміну від напруженості поля, яка при накладанні полів додається векторно. От за цих причин визначення потенціалів набагато простіше за визначення напруженості. Або для роботи:

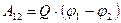
(21)

Тобто, робота, виконувана силами поля над зарядом 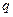дорівнює добутку величини заряду 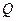на різницю потенціалів у початковій та кінцевій точках (тобто на величину зменшення потенційної енергії поля).

Можна просто позначити величину скалярного добутку через :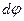

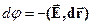
(22)

Але тоді постає питання щодо появи знаку „мінус”, яке можливо вирішити тільки пізніше, тобто просто дати йому якесь пояснення. Тоді елементарну роботу матиме вигляд:

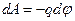
(23)

За фізичним змістом величина 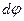є роботою по переміщенню заряду в електричному полі, розрахована на одиничний пробний заряд:

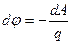
(24)

Величина 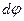має назву „різниця потенціалів поміж точками 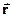та 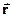+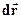”. Отже:

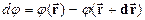
(25)

У свою чергу 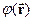- є потенціалом електричного поля початкової точки 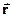, а - потенціал поля в кінцевій точці (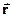+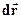). Повну роботу з переміщення заряду знайдемо інтегруванням:

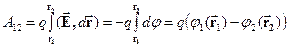
(26)

Отже, робота сил електростатичного поля залежить лише від різниці потенціалів у цих точках та величини пробного заряду. Цей факт є доказом потенційності електростатичного силового поля та консервативності електростатичних сил.

Якщо об’єднати всі точки електричного поля, які мають однаковий потенціал, то така поверхня має назву еквіпотенційної поверхні, або поверхні рівного потенціалу. Переміщення заряду вздовж такої поверхні не потребує роботи, оскільки всі точки поверхні мають однаковий потенціал і різниця потенціалів між точками поверхні дорівнює нулю. Робота буде ненульовою лише при переміщенні заряду з однієї такої поверхні на іншу поверхню (з іншим потенціалом).

Раніше ми встановили, що електричне поле можна описати чи за допомогою векторної величини 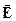(напруженості електричного поля), чи за допомогою скалярної величини 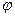(потенціалу електричного поля). Поміж цими величинами повинен існувати зв’язок:

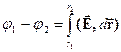
(27)

Чи у наступному вигляді:

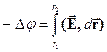
(28)

Для випадку малих 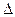маємо право на в лівій частині перед 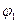поставити знак диференціалу, а в правій опустити знак інтегралу; додатково перенесемо знак мінус в праву частину рівності:

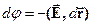
(29)

У випадку скалярного добутку двох векторів маємо право представити напруженість електричного поля у наступному вигляді:

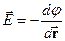
(30)

Радіус-вектор 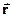, як і будь-який вектор можна розкласти на компоненти, тобто: 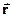=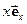++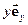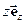,де 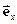, , 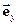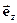- орти (одиничні вектори) відповідних осей, 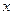, , 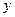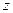- проекції вектора 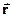на відповідні координатні осі.

З курсу вищої математики відомо, що похідну, подібну до (30) можна представити сумою часткових похідних, помножених на відповідний орт:

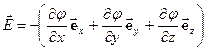
(31)

Вираз 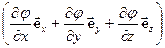називають градієнтом потенціалу 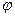і позначають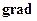 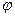або 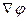. Отже, в загальному випадку градієнтом є оператор, який діє на скалярні функції типу потенціалу (температури, потенціальної енергії і т.п.)

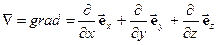
(32)

Чи з урахуванням позначення градієнта:

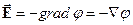
(31а)

Отже, результатом дії оператору градієнта буде вектор, який спрямований в бік зростання скалярної функції (тобто він вказує напрям зростання скалярної функції), в нашому випадку – потенціалу, а знак „мінус” таким чином вказує на те, що напрями векторів напруженості і градієнта потенціалу протилежні.

Вирази (31) і (31а) є так званою диференціальною формою зв’язку між напруженістю та потенціалом електричного поля.

Силові лінії електростатичного поля завжди нормальні до еквіпотенційних поверхонь (тобто перпендикулярні до дотичної площини в кожній точці такої поверхні). Отже, маючи картину силових ліній поля можна побудувати еквіпотенційні поверхні, і навпаки. Еквіпотенційні поверхні окремого одиничного точкового позитивного або негативного зряду у відсутності інших зарядів будуть мати вигляд концентричних кіл. Але еквіпотенційні поверхні системи хоча б двох зарядів будуть мати складніший характер.

ü Теорема Остроградського-Гауса

Рис.6а

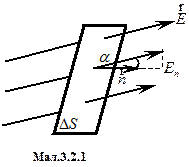На основі закону Кулона (7) і принципу суперпозиції (9) можна визначити напруженість практично будь-якої системи нерухомих зарядів. Однак такий спосіб розв’язання задач електростатики часто призводить до надто громіздких обчислень. Задача істотно спрощується, якщо скористатися деякими теоремами про загальні властивості електростатичного поля. Однією з таких теорем є теорема Остроградського-Гаусса. Ця теорема має також принципове значення. Математичний запис основного закону електростатики у формі (7) відповідає теорії далекодії. Теорема Остроградського-Гаусса дає можливість звести основні рівняння електростатики до диференціальної форми і узгодити їх, таким чином з теорією близькодії.

Теорема Остроградського-Гаусса пов’язує потік вектора напруженості електростатичного поля через довільну замкнену поверхню з зарядом, який охоплюється цією поверхнею.

Нехай дано однорідне поле напруженістю 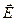. Розмістимо в цьому полі плоску поверхню 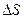, нормаль до якої 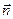утворює кут з вектором 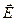(Рис.6а). Величину

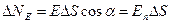
(32)

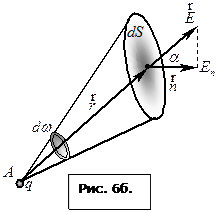Називають потоком вектора 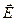через поверхню 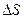(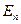– проекція 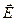на нормаль 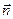). Потік може бути додатним або від’ємним залежно від знака проекції 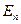, який визначається знаком 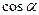. Вибір додатного напряму 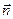умовний (додатною вважають зовнішню нормаль до поверхні ).

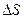Якщо поле неоднорідне і поверхня не плоска, то уявно її розбивають на елементи 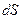, які можна наближено вважати плоскими, а поле в її межах – однорідним (рис.6б). Тоді елементарний потік вектора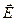

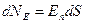
(33)

А повний потік через поверхню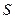

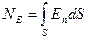
(33а)

Для доведення теореми Остроградського-Гаусса обчислимо спочатку потік вектора напруженості електростатичного поля, створюваного точковим зарядом, через довільну замкнену поверхню.

Нехай точковий заряд 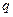розміщений у точці А (рис.6), а елемент поверхні 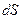міститься на відстані 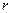. Тоді

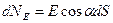
Скориставшись формулою (32), отримуємо

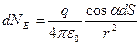
(34)

Де 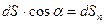– проекція 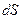на поверхню сфери радіуса 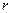. Крім того, 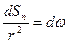– тілесний кут, під яким з точки А видно елемент поверхні. Тоді (34) можна переписати:

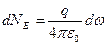
(34а)

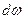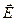Вважатимемо додатним, якщо кут між напрямами і 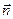гострий, і від’ємним, якщо кут тупий.

Обчислимо повний потік вектора 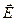через довільну замкнену поверхню. Розглянемо два випадки.

Точковий заряд міститься всередині замкненої поверхні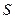

Довільний конус з вершиною в точці розміщення заряду 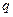і тілесним кутом 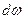виокремить на заданій поверхні одну елементарну поверхню 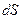. Незалежно від форми поверхні елементарний потік вектора 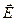визначатиметься лише потоком через елементарну площу 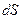, оскільки при наявності інших перерізів потоки через них будуть однакові за величиною, протилежні за знаком і їхня сума дорівнюватиме нулю. Отже, в цьому випадку

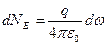
А повний потік через довільну замкнену поверхню 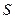, яка охоплює даний точковий заряд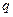

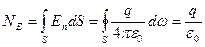
(35)

Оскільки 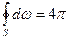стерадіанів.

Якщо поверхня 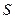охоплює систему точкових зарядів, то

(35а)

ü Точковий заряд міститься зовні від замкненої поверхні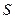

У цьому разі довільний конус з вершиною в місці розташування точкового заряду 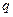і тілесним кутом 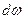виокремить завжди парну кількість елементарних поверхонь 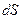на замкненій поверхні 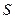. Елементарні потоки 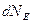через кожну з цих поверхонь 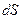будуть однакові за величиною, але протилежні за знаками. Тому їхній сумарний елементарний потік дорівнює нулю, а отже, і повний потік

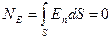
(35б)

Обидва випадки (заряди всередині замкненої поверхні і заряди поза поверхнею) описуються формулою (35а), яка є математичним виразом теореми Остроградського-Гаусса:

У випадку об’ємних і поверхневих зарядів

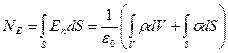
(35в)

Позитивному заряду відповідає додатний потік напруженості, негативному – від’ємний. Отже, заряди є своєрідними джерелами і стоками потоку напруженості поля (позитивні заряди – джерелами, негативні – стоками поля).

Заряд, який охоплюється паралелепіпедом зі сторонами 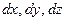при рівномірному його розподілі з об’ємною густиною 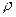, дорівнює 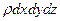. Тоді за теоремою Остроградського-Гаусса (35а)

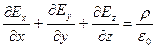
(36)

Співвідношення (36) виражає теорему Остроградського-Гаусса у диференціальній формі. Оскільки розміри паралелепіпеда 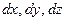нескінченно малі, то можна прийняти, що значення вектора 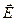на поверхні цього паралелепіпеда і заряд, який охоплюється поверхнею, по суті стосуються тієї самої точки.

За теоремою Остроградського-Гаусса у формі (35в) для об’ємних зарядів 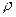з урахуванням того, що 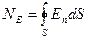, можна записати

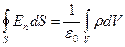
(37)

Де 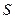– довільна замкнена поверхня, 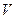– обмежений нею об’єм.

У векторному аналізі доведено, що границя відношення потоку будь-якого вектора 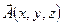, визначеного в усіх точках векторного поля, через замкнену поверхню 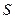до величини об’єму 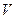, обмеженого цією поверхнею, при 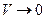не залежить від форми 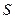. Границю цього відношення називають розходженням, чи дивергенцією, вектора 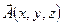в точці, в яку стягується об’єм 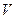, і позначають символом 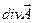. За означенням

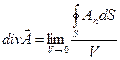
За теоремою Гаусса 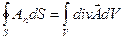. Для вектора напруженості електричного поля маємо:

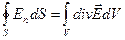
(38)

Чи з урахуванням (37)

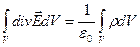
(39)

Оскільки 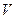– довільний об’єм, то очевидна рівність

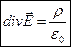
(40)

Порівнюючи з (36) маємо:

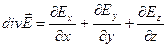
(41)

Формула (41) дає можливість обчислити дивергенцію в декартових координатах. Дивергенція фізично характеризує потужність джерел чи стоків.

ü Поняття електроємності. Конденсатори. Способи їх з’єднання

Заряджений провідник містить або надлишок електронів (тоді його заряд від’ємний, негативний), або їх нестачу (тоді його заряд позитивний, додатній). Додатковий заряд буде рівномірно розподілений.

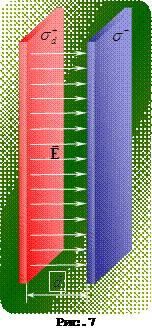Застосуємо теорему Гауса для електричного поля зарядженої площини, показаної на рис.7. Припустимо, що поверхнею інтегрування є циліндр з площею перерізу 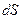. Тоді потік електричного поля крізь бокову поверхню є нульовим (силові лінії є паралельними до бокової поверхні циліндру), а повний потік складається з потоку крізь два перерізи площі 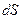. Отже, з теореми Гауса маємо, враховуючи перпендикулярність силових ліній до перерізу циліндра:

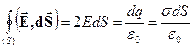
(42)

де 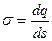- поверхнева густина заряду. З (42) легко отримати простий вираз для напруженості електричного поля поблизу від зарядженої площини:

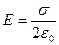
(43)

Таким чином, напруженість електричного поля поблизу від рівномірно зарядженої плоскої поверхні металу прямо пропорційна поверхневій густині заряду і не залежить від відстані до поверхні (таке поле є, зрозуміло, однорідним).

Рис.8.

Розглянемо дві рівномірно заряджені металеві пластини, відстань поміж якими (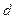) є малою порівняно з розмірами пластин (рис.8), причому обидві вони заряджені однаковим, але різнойменним зарядом, з однаковою густиною 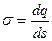. Таку систему називають плоским конденсатором. Напруженість поля поміж пластинами конденсатора вдвічі більша від (43), оскільки є суперпозицією двох полів від двох рівномірно заряджених пластин:

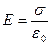
(44)

Різниця потенціалів поміж пластинами (її називають також напругою) дорівнює добутку напруженості поля на відстань поміж пластинами:

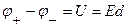
(45)

З урахуванням виразу для густини заряду 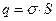(де 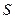- площа поверхні пластин конденсатору), можна отримати зв’язок поміж зарядом та напругою на конденсаторі:

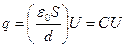
(46)

де коефіцієнт пропорційності поміж зарядом конденсатора (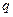) та напругою поміж пластинами (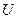) має назву електроємності конденсатора ().

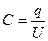Таблиця 1. Типи конденсаторів та їх ємності

Тип конденсатора	Вигляд	Ємність	Примітки
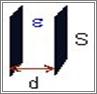
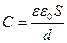
Плоский			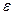- діелектрична проникливість діелектрика, вміщеного поміж обкладинками конденсатора
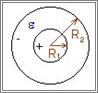
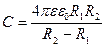
Сферичний			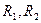- радіуси внутрішньої та зовнішньої обкладинок конденсатору
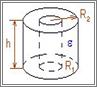
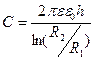
Циліндричний			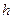- висота циліндричних обкладинок

Для випадку плоского вакуумного конденсатора маємо:

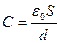
(47)

тобто електроємність плоского конденсатора прямо пропорційна площі обкладинок і обернено пропорційна відстані поміж ними.

Енергію, яку запасає разом із електричним зарядом конденсатор, неважко підрахувати, виходячи із зв’язку роботи та різниці потенціалів:

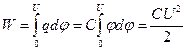
(48)

Деякі типи конденсаторів та їх ємності показані у таблиці 1.

Для отримання бажаної ємності конденсатори з’єднують у батареї. З’єднання може бути паралельним, послідовним чи змішаним.

При послідовному з’єднанні заряд на всіх обкла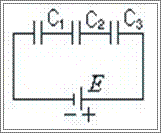динках однаковий а загальна напруга батареї є сумою напруг:

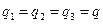
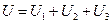
Звідки неважко отримати, що складати в цьому випадку треба обернені ємності:

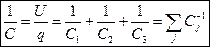
(49)

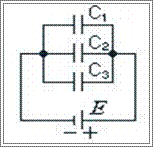При паралельному з’єднанні, навпаки, загальний заряд є сумою зарядів, тоді як напруга 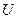є однаковою для всіх конденсаторів. Отже складаються ємності:

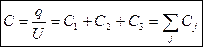
(50)

Формули (49,50) можна застосовувати для довільної кількості конденсаторів, з’єднаних у батарею.

Ємність конденсаторів вимірюється в 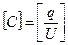=Кл/В=Ф (фарад).

Так, наприклад, ємність в 1 Ф мала б відокремлена куля радіуса 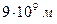, тобто радіуса, в 1500 разів більшого ніж радіус Землі. Відповідно, фарад – дуже велика величина. Доречи, куля розміром у Землю мала б ємність усього .

Якщо напругу на конденсаторі зробити надто великою, то може статися „пробій” – між обкладками конденсатора виникне іскра, що призведе до його псування. Тому кожен конденсатор характеризується не лише своєю ємністю, але й максимальною напругою.

Рекомендована література:

1. Кудрявцев П.С. Курс истории физики. – М.: Просвещение, 1982.–448 С.

2. Дягилев Ф.М. Из истории физики и жизни ее творцов. – М.: Просвещение, 1986.–255 С.

3. Хромов Ю.А. Физики: биографический справочник. – К.: Наукова думка, 1977.–511 С.

4. Хрестоматия по физике: учеб пособие по физике для уч-ся 8-10 классов. – М.: Просвещение, 1982.–223 С.

5. Савельев И.В. Курс общей физики. Том II. Электричечтво – М.: Наука, 1988 – с.11-34.

6. Кучерук І.М., Горбачук І.Т. Загальна фізика: Електрика і магнетизм. – К.: Вища шк., 1995. – с.3-26.

7. Бушок Г.Ф., Левандовський В.В., Півень Г.Ф. Курс фізики. Кн. 1. Фізичні основи механіки. Електрика і магнетизм. – К.: Либідь, 2001. – с.220-230.

8. Детлаф А.А., Яворский Б.М. Курс физики: – М.: Высш.шк.., 1989. – с.154-162.

9. Калашников С.Г. Электричество. – М.:Наука, 1985. – 576 С.

Дата добавления: 2014-01-04