Лекция 4

Схема повторения испытаний. Формула Бернулли

Рассмотрим серию из п испытаний, в каждом из которых событие А появляется с одной и той же вероятностью р, причем результат каждого испытания не зависит от результатов остальных. Подобная постановка задачи называется схемой повторения испытаний. Найдем вероятность того, что в такой серии событие А произойдет ровно k раз (не важно, в какой последовательности). Интересующее нас событие представляет собой сумму равновозможных несовместных событий, заключающихся в том, что А произошло в некоторых k испытаниях и не произошло в остальных (п – k) испытаниях. Число таких событий равно числу сочетаний из п по k, то есть 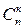, а вероятность каждого из них равна умножению вероятностей независимых событий: , где q = 1 – p – вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли:

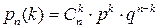, где k = 0,1,2,…, n (1) – формула Бернулли.

Учитывая, что q = 1 – p, формулу Бернулли можно записать в виде:

.

Сумма вероятностей по всем 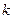от 0 до 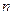удовлетворяют условию: .

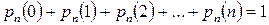Задача 1. Пусть монету бросают 8 раз. Какова вероятность того, что «герб» выпадет 5 раз?

Решение. Применим формулу Бернулли: , где

n = 8, k = 5 (число успехов), 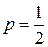. Тогда

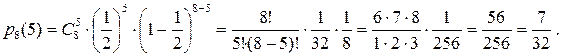
Задача 2. Для получения приза нужно собрать 5 изделий с особым знаком на этикетке. Найти вероятность того, что придется купить 10 изделий, если этикетки с этим знаком имеют 5% изделий.

Решение. Из постановки задачи следует, что последнее купленное изделие имеет особый знак. Следовательно, из предыдущих девяти эти знаки имели 4 изделия. Найдем вероятность этого по формуле Бернулли: 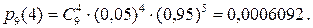. Тогда р = 0,0006092·0,05 = 0,0000304.

Дата добавления: 2014-01-04