Формула Пуассона или формула редких явлений

Формула Бернулли требует громоздких расчетов при большом количестве испытаний. Можно получить более удобную для расчетов приближенную формулу, если при большом числе испытаний вероятность появления А в одном опыте мала, а произведение 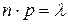сохраняет постоянное значение для разных серий опытов (то есть среднее число появлений события А в разных сериях испытаний остается неизменным).

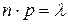Теорема. Пусть производится n независимых опытов. В результате каждого опыта событие А может наступить с вероятностью р. Пусть , произведение постоянно, тогда справедлива формула: , где k не меняется.

Или 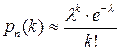– формула Пуассона, где .

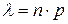Доказательство. Применим формулу Бернулли:

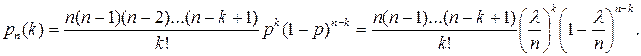
Найдем предел полученного выражения при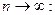

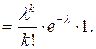
Таким образом, формула Пуассона позволяет найти вероятность k появлений события А для массовых (когда п велико) и редких (когда р мало) событий.

Для вычисления дробей существуют специальные таблицы (см. Приложение 1). Чтобы ими пользоваться, надо знать и (число успехов).

Задача. Прядильщица обслуживает 1000 веретён. Вероятность обрыва нити на одном веретене в течение 1 минуты равна 0,004. Найти вероятность того, что в течение 1 минуты обрыв произойдет на 5-ти веретенах.

Решение. По условию, , , 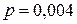. Найдем 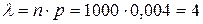. По формуле Пуассона 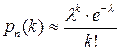искомая вероятность приближенно равна: .

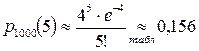Дата добавления: 2014-01-04