
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ 6. §15 Равномерный закон распределения вероятностей (равномерное распределение на отрезке)
|
|
|
|
§15 Равномерный закон распределения вероятностей
(равномерное распределение на отрезке)
При решении практических задач зачастую точно найти закон распределения случайной величины довольно сложно. Однако, все происходящие процессы, связанные со случайными величинами, можно разделить на несколько типов, каждому из которых можно поставить в соответствие какой – либо закон распределения. Выше были рассмотрены некоторые типы распределений дискретной случайной величины, такие как биномиальное распределение и распределение Пуассона.
Рассмотрим теперь некоторые типы законов распределения для непрерывной случайной величины.
Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [ a, b ], если на этом отрезке плотность вероятности случайной величины постоянна, а вне его равна нулю: 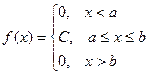 .
.
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения.
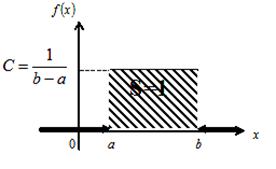
Получаем 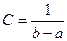 . Таким образом, плотность вероятности случайной величины примет вид:
. Таким образом, плотность вероятности случайной величины примет вид: 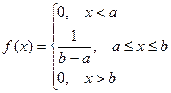 .
.
Теорема (основное свойство равномерного распределения). Пусть случайная величина X равномерно распределена на отрезке [a, b]. Пусть отрезок 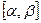 полностью лежит в отрезке [a, b], тогда справедлива формула:
полностью лежит в отрезке [a, b], тогда справедлива формула:
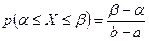 .
.
Эта теорема утверждает, что вероятность попадания значений случайной величины в отрезок 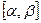 зависит только от длины этого отрезка и не зависит от его положения на оси OX. Поэтому о такой случайной величине говорят, что она равномерно распределена на отрезке [ a, b ].
зависит только от длины этого отрезка и не зависит от его положения на оси OX. Поэтому о такой случайной величине говорят, что она равномерно распределена на отрезке [ a, b ].
Найдем функцию распределения F(x) в случае равномерного распределения на отрезке [a,b].
Функция распределения может быть легко найдена, если известна плотность вероятности, по формуле:  . По условию
. По условию
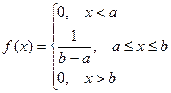 .
.
 | |||
 | |||
При 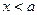 ,
,  .
.
 |
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 776; Нарушение авторских прав?; Мы поможем в написании вашей работы!