Показательный закон распределения вероятностей

2.

1.

При ,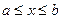

При ,

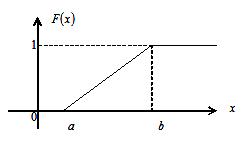
Окончательно получаем, что функция распределения в случае равномерного распределения на отрезке имеет вид:

Для того чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы ее значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны (равновозможны).

Пример 1. Цена деления шкалы амперметра равна 0,1 А. Показания округляются до ближайшего целого деления. Найти вероятность того, что при округлении будет сделана ошибка, непревышающая по абсолютной величине 0, 02 А.

Решение. Пусть X – ошибка округления. Считаем, что она имеет равномерный закон распределения на отрезке (по умолчанию) 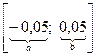. Нас интересует ошибка 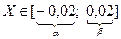. Тогда вероятность найдем по формуле: 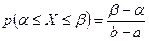. Получим

Пример 2. Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут.

Решение. Время ожидания является случайной величиной, равномерно распределенной в интервале [0, 5]. Тогда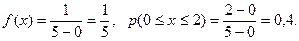

§16 Нормальный закон распределения вероятностей
(или нормальное распределение на прямой)

Определение. Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения вероятности имеет вид:

, (1)

где числа 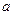и 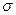называются параметрами нормального распределения. График функции 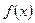(или плотности нормального распределения) называют нормальной кривой (кривой Гаусса).

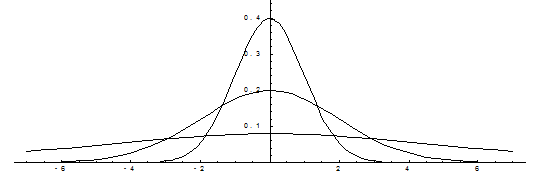
Замечание. Таким образом, нормальное распределение определяется двумя параметрами: а и σ. График функции 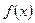симметричен относительно прямой .

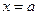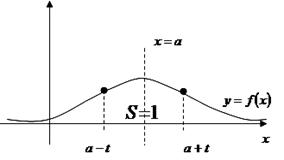
для любого t.

Форма графика зависит от параметра 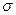, чем больше 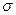, тем шире и ниже график.

Теорема (основное свойство нормального распределения). Пусть случайная величина X имеет нормальный закон распределения с параметрами а и σ, тогда справедлива формула: , где 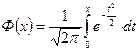– функция Лапласа.

Теорема (правило трёх сигм). Пусть случайная величина X имеет нормальный закон распределения с параметрами а и σ, тогда справедлива формула: .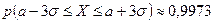

Другими словами, тот факт, что значение случайной величины, распределённой по нормальному закону попадает в промежуток [] является практически достоверным событием.

На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

Функция распределения для нормального закона имеет вид:

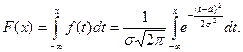
Перед нами так называемый «неберущийся» интеграл, который невозможно выразить через элементарные функции. Поэтому для вычисления значений F (x) приходится пользоваться таблицами. Они составлены для случая, когда, а = 0, а σ = 1.

Замечание. Функцию распределения для произвольных параметров можно выразить через функцию Лапласа, если сделать замену: , тогда .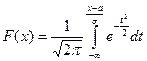

Пример. Случайная величина Х имеет нормальное распределение с параметрами, а = 3, 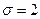. Найти вероятность того, что она примет значение из интервала (4; 8).

Решение. Применим основное свойство нормального распределения (см. теорему выше), получим:

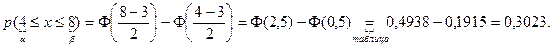
Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

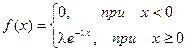, где l - положительное число.

Найдем закон распределения: 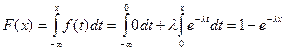. Следовательно, функция распределения для показательного закона имеет вид:

.

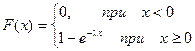Графики функции распределения и плотности распределения вероятности:

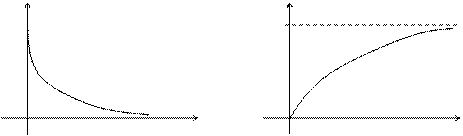f (x) F (x)

1

0 x 0 x

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал (a, b).

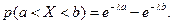
Пример. Непрерывная случайная величина X распределена по показательному закону

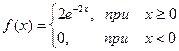. Найти вероятность того, что в результате испытания X попадает в интервал (0,3; 1).

Решение. По условию, 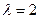. Воспользуемся выше записанной формулой.

Дата добавления: 2014-01-04