Математическое ожидание дискретной случайной величины

Основные числовые характеристики случайных величин

ЛЕКЦИЯ 7

Если случайная величина дискретная, то ее удобно задавать с помощью таблицы. Непрерывные случайные величины чаще всего задаются плотностью вероятности.

Закон распределения полностью характеризует случайную величину. Однако когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.

Иногда для того, чтобы установить закон распределения случайной величины, достаточно задать несколько ее числовых характеристик: математическое ожидание, дисперсию, среднее квадратическое отклонение. К числу важных числовых характеристик относится математическое ожидание.

Определение. Пусть дискретная случайная величина X задана таблицей:

xi	x 1	x 2	…	xn	…
pi	p 1	p 2	…	pn	…

Математическим ожиданием этой случайной величины называется число, которое обозначается 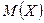и находится по формуле: . При этом ряд должен сходиться абсолютно (то есть, чтобы сумма ряда не зависела от порядка слагаемых).

Замечание 1. Данный ряд может и расходиться, то соответствующая случайная величина может и не иметь математического ожидания.

Замечание 2. Из определения следует, что математическое ожидание дискретной случайной величины есть постоянная величина.

Замечание 3. С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Пример. Найти математическое ожидание случайной величины X, зная закон ее распределения:

xi
pi	0,45	0,4	0,1	0,05

Решение. Математическое ожидание находим по формуле:

.

Теорема. Пусть случайная величина X распределена по закону Пуассона с параметром , тогда .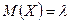

Теорему примем без доказательства.

Дата добавления: 2014-01-04