Эмпирическая функция распределения

Интервальные таблицы частот

ЛЕКЦИЯ 9

При большом объеме выборки ее элементы объединяют в группы (разряды, интервалы), представляя результаты опытов в виде интервального статистического ряда. Для этого весь диапазон значений случайной величины 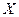(от до 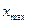) разбивают на k интервалов одинаковой длины 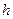(обычно k меняется от 5 до 20) и подсчитывают частоты 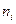(или относительные частоты 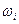) значений выборки, попавших в интервалы. Величина называется плотностью частоты, а – плотностью относительной частоты.

Пусть – середина 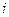-го интервала, 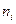– число элементов выборки, попавших в 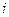-й интервал (при этом элемент, совпавший с верхней границей интервала, относится к последующему интервалу). Таким образом, получим группированный статистический ряд, в верхней строке которого записаны середины соответствующих интервалов , а в нижней – частоты:

			…
			…

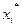
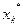
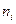
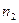
Пример 1. Выборка, полученная в результате статистического наблюдения (единицы измерения опускаем) – 3,14; 1,41; 2,87; 3,62; 2,71; 3,95.

Решение. Ранжированный вариационный ряд:

, где

Соответствующее статистическое распределение :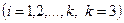

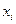
	1-2	2-3	3-4

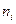
Для графического представления интервальных статистических распределений принято использовать гистограмму относительных частот.

Гистограммой относительных частот интервального статистического ряда называется ступенчатая фигура, составленная из прямоугольников, построенных на интервалах группировки длины 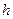и высоты так, что площадь каждого прямоугольника равна относительной частоте .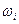

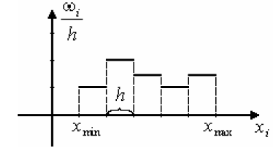
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки длиной параллельно оси ординат. Очевидно, площадь 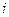-го частичного прямоугольника равна 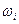– относительной частоте вариант, попавших в 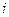-ый интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот (т.е. равна 1), а площадь гистограммы частот равна объему выборки .

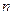Пример 2. Имеется распределение 80 предприятий по числу работающих на них человек:

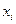
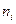
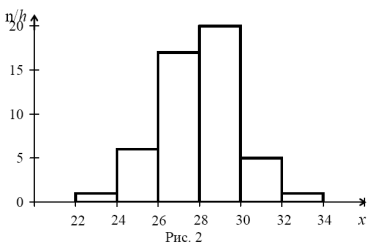
Решение. Признак Х – число работающих (чел.) на предприятии. В данной задаче признак Х является дискретным. Поскольку различных значений признака сравнительно немного – k = 7, применять интервальный ряд для представления статистического распределения нецелесообразно (в прикладной статистике в подобных задачах часто используют именно интервальный ряд). Ряд распределения – дискретный. Построим полигон распределения частот (рис. 1).

Пример 3. Дано распределение 100 рабочих по затратам времени на обработку одной детали (мин):

Решение. Признак Х – затраты времени на обработку одной детали (мин). Признак Х – непрерывный, ряд распределения – интервальный. Построим гистограмму частот (рис. 2), предварительно определив 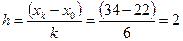и плотность частоты :

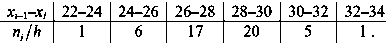
Пусть известно статистическое распределение (или статистический ряд) количественного признака 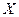; – число наблюдений, при которых наблюдалось значение признака, меньшее , т.е. ; 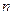– общее число наблюдений (объём выборки). Тогда относительная частота события есть 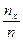. При изменении меняется и 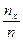, т.е. относительная частота 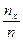является функцией x. Так как эта функция находится эмпирическим (т.е. опытным) путём, то её называют эмпирической.

Определение. Эмпирической функцией распределения (функцией распределения выборки) называется функция (1), определяющая для каждого значения x относительную частоту события .
В (1) – число вариант, меньших x (, 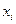- варианты, 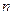– объём выборки). Поэтому для расчетов удобна формула вида:

.

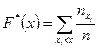Тогда, например, 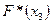означает 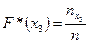, где 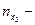число вариант, меньших или в табличной форме:

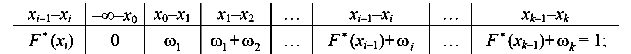
Функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической 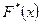и теоретической функциями распределения состоит в том, что определяет вероятность события , а относительную частоту того же события. 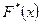обладает всеми свойствами .

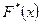Свойства эмпирической функции распределения :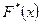

Свойство 1. Значения 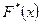принадлежат ; ;

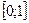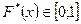Свойство 2. неубывающая функция;

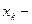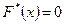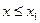Свойство 3. Если наименьшая варианта, а наибольшая варианта, то для , для ;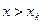

Свойство 4. 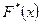непрерывная слева функция.

Дата добавления: 2014-01-04