Сравнение двух средних генеральных совокупностей, дисперсии которых известны (неизвестны)

1) Генеральные совокупности Х и Y распределены нормально, причем известны их

дисперсии. Из этих генеральных совокупностей извлечены выборки объемов соответственно т и п, для которых найдены выборочные средние и . При заданном уровне значимости 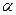проверяется нулевая гипотеза о равенстве математических ожиданий генеральных совокупностей: Н_о: М (Х) = М (Y).

Статистическим критерием для проверки этой гипотезы является нормированная нормально распределенная случайная величина

Наблюдаемое значение критерия .
Вид критической области зависит от типа конкурирующей гипотезы:

a. – критическая область двусторонняя, z_кр определяется как аргумент функции Лапласа, при котором и критическая область задается неравенством .

b. – критическая область правосторонняя, z_кр определяется как аргумент функции Лапласа, при котором и критическая область определяется неравенством .

c. – критическая область левосторонняя, заданная неравенством , где z_кр вычисляется так же, как в предыдущем случае.

2) Имеются две независимые выборки большого объема, извлеченные из

генеральных совокупностей, законы распределения и дисперсии которых неизвестны. При этом для объема выборки, не меньшего 30, можно считать, что выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий (следовательно, считаем известными приближенные значения генеральных дисперсий). Тогда задача сводится к предыдущей, и статистический критерий имеет вид:

Наблюдаемое значение критерия вычисляется по формуле:

При этом выбор вида критической области и определение критических точек проводятся так же, как в пункте 1.

3) Генеральные совокупности распределены нормально, причем их дисперсии неизвестны, а объем выборок т и п мал (следовательно, нельзя получить хорошие оценки генеральных дисперсий). Если предположить, что генеральные дисперсии равны, то в качестве критерия для проверки нулевой гипотезы служит случайная величина

,

имеющая при справедливости нулевой гипотезы распределение Стьюдента с k = n + m – 2 степенями свободы. Наблюдаемое значение критерия вычисляется по формуле

.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

a. – критическая область двусторонняя, задаваемая неравенством _., где 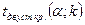находится из таблицы критических точек распределения Стьюдента.

b. – критическая область правосторонняя, определяемая условием 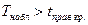_.. Критическая точка вновь находится по таблице критических точек распределения Стьюдента.

c. – критическая область левосторонняя,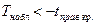

Пример. Имеются независимые выборки значений нормально распределенных случайных величин

Х: 2, 2, 3, 3, 4, 4, 4, 5, 5, 6 и Y: 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 7, 8, 9.

Требуется проверить для уровня значимости 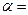0,1 при условии равенства генеральных дисперсий нулевую гипотезу при конкурирующей гипотезе .

Решение. Объемы выборок т = 10, п = 15. Вычислим выборочные средние и исправленные выборочные дисперсии: . Вычислим наблюдаемое значение критерия: . Критическая область – двусторонняя, t_{двуст.кр.} (0,1; 23) = 1,71 (из таблицы критических точек распределения Стьюдента). Итак, , следовательно, нет оснований отвергнуть нулевую гипотезу – можно считать, что математические ожидания генеральных совокупностей равны.

Дата добавления: 2014-01-04