Импульсная диаграмма и кинематика ядерных реакций

Напомним, что кинематикой называют раздел механики, посвященный изучению геометрических свойств движения тел без учета действующих на тела сил. Движение любого тела в кинематике изучают по отношению к некоторой системе координат, позволяющей определить относительное положение движущегося объекта в любой момент времени. В ядерной физике обычно используют две системы координат: лабораторную (ЛСК), связанную с ядром-мишенью, и систему центра инерции (СЦИ), определение которой будет дано ниже.

Кинематическая схема ядерной реакции и связь между энергиями, импульсами и углами вылета частиц в ЛСК и СЦИ имеет наглядное графическое представление и может быть проанализирована с помощью импульсной диаграммы (векторной диаграммы импульсов). Построение импульсной диаграммы основано на применении законов сохранения энергии и импульса.

Пусть имеется произвольная инерциальная система координат К', которая движется относительно ЛСК со скоростью 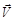. Скорости любой из i = 1, 2, 3,..., N частиц в ЛСК и К' ‑системе связаны следующим образом:

.

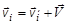(4.5.1)

Закон сохранения импульса для совокупности из i = 1, 2, 3,..., N – частиц записывается следующим образом:

,

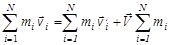(4.5.2)

так как ЛСК и К' ‑система – системы инерциальные. Первое слагаемое в правой части есть суммарный импульс частиц в К' -системе, а второе - определяет импульс движения К' -системы как целого в ЛСК, который носит название переносного импульса. Соответствующим выбором вектора скорости 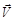можно добиться, чтобы суммарный импульс частиц в К' -системе был равен нулю:

.

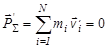(4.5.3)

Система координат, в которой суммарный импульс 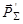частиц равен нулю, называется системой центра инерции (СЦИ). Условимся величины, относящиеся к СЦИ, обозначать сверху значком “~” (тильда). Положив в (4.5.2) 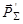= 0, найдем скорость движения СЦИ относительно ЛСК:

.

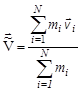(4.5.4)

Обратимся к рассмотрению процесса (4.1.1). Пусть в ЛСК частица а движется со скоростью 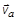, а ядро-мишень А – покоится. Используя (4.5.4) найдем скорость движения СЦИ (или составного ядра, если таковое образуется) относительно ЛСК:

.

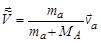(4.5.5)

Из сотношения (4.5.2) и (4.5.5) следует, что переносной импульс СЦИ в ЛСК равен импульсу частицы а в ЛСК:

.

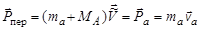(4.5.6)

Поместим ядро-мишень А в начале координат (рис. 4.5.1). Если частица а движется вдоль оси Х навстречу частице А, то из (4.5.5) следует, что положение центра инерции 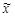на оси Х в любой момент времени связано следующим образом с положением х_а частицы а:

,

(4.5.7)

т.к. скорость движения вдоль оси Х есть dx/dt. На рисунке видно, что центр инерции всегда располагается между частицами а и А, двигаясь вдоль оси Х со скоростью 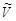, относительно ядра-мишени А.

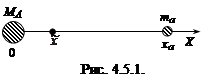Найдем с помощью (4.5.1) и (4.5.5) скорости движения частицы а и ядра-мишени А в СЦИ и соответствующие им импульсы:

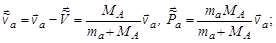
	(4.5.8)
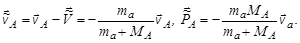
	(4.5.9)

Таким образом, импульсы частиц а и А в СЦИ равны друг другу и противоположно направлены, как и должно быть.

Используя (4.5.8) и (4.5.9), выразим суммарную кинетическую энергию 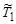частиц a и А в СЦИ через кинетическую энергию Т_a частицы a в ЛСК в нерелятивистском приближении

.

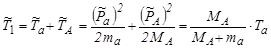(4.5.10)

Кинетическая энергия 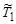есть энергия взаимного движения частиц а и А и она меньше суммарной кинетической энергии Т ₁ = Т_а на величину

,

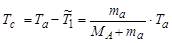(4.5.11)

которая есть ничто иное, как кинетическая энергия движения СЦИ (промежуточного ядра) относительно ЛСК. Действительно, кинетическая энергия движения СЦИ равна

.

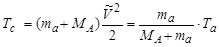(4.5.12)

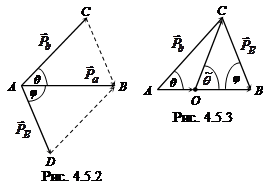Очевидно, что кинетическая энергия (4.5.12) движения центра инерции не может перейти во внутреннюю энергию частиц и не может быть использована в ядерной реакции.

На этом закончим рассмотрение входного канала процесса (4.1.1) и перейдем к рассмотрению выходного канала.

В ЛСК сумма импульсов частиц b и В, образовавшихся в результате ядерной реакции, по закону сохранения импульса равна импульсу налетающей частицы а:

.

(4.5.13)

На рис. 4.5.2 представлена схема одного из возможных вариантов разлета продуктов реакции, а на рис. 4.5.3 графический аналог векторного уравнения (4.5.13). На этих рисунках θ и φ – углы вылета частиц b и B относительно направления движения частицы а. Очевидно, что отрезок СВ на рис. 4.5.3 равен импульсу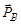на рис. 4.5.2. Остальные величины совпадают с рис. 4.5.2. Поэтому в дальнейшем будем рассматривать векторный треугольник АСВ (рис. 4.5.3).

Так как сумма импульсов переносного движения частиц b и В по закону сохранения импульса должна быть равна импульсу 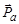, т.е.

,

(4.5.14)

а отношение

,

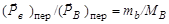(4.5.15)

то точка О на рис. 4.5.3 делит отрезок АВ =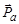на отрезки АО = 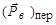и ОВ = 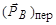в соответствии с (4.5.15).

Очевидно, что ОС =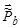, так как

,

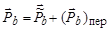(4.5.16)

а угол 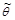на рис. 4.5.3 - есть угол вылета частицы b в СЦИ.

Вектор 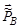, согласно свойствам СЦИ, равен вектору 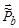по абсолютной величине:

,

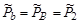(4.5.17)

и направлен в противоположную сторону, т.е. частицы b и B в СЦИ разлетаются с равными и противоположными импульсами.

Вычислим величину 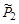. Из закона сохранения энергии:

,

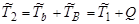(4.5.18)

Или, учитывая (4.5.10):

.

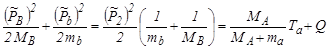(4.5.19)

Из последнего уравнения находим

,

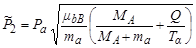(4.5.20)

где

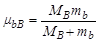
(4.5.21)

- есть приведенная масса частиц b и B.

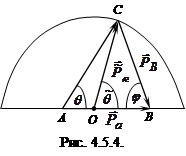Полученные результаты можно использовать для построения векторной диаграммы импульсов, графически связывающей импульсы в ЛСК и СЦИ. Для этого отрезок, изображающий импульс Р_а (рис. 4.5.4), надо разделить точкой 0 в отношении 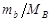. Затем из этой точки радиусом 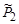(4.5.20) провести окружность. Тогда, если известна хотя бы одна из величин Р_b, Р_B, θ, φ,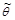, из диаграммы можно определить графически все остальные.

В случае упругого рассеяния частицы выходного канала тождественны частицам входного канала и из (4.5.20) следует, что

.

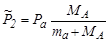(4.5.22)

Далее построение векторной диаграммы импульсов для упругого рассеяния не имеет особенностей и выполняется аналогичным образом.

Приведем теперь несколько примеров применения законов сохранения в ядерных реакциях.

Определим энергетический порог для эндоэнергетической реакции. Используя систему центра инерции и формулу (4.4.6), имеем

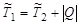
(4.5.22)

и, следовательно, минимальное значение 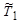(когда 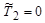) составит

.

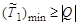(4.5.23)

Используя (4.5.10) найдем минимальную кинетическую энергию частицы а в лабораторной системе координат (ЛСК):

.

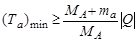(4.5.24)

Полученное значение кинетической энергии бомбардирующей частицы в ЛСК, при котором становится возможным протекание эндоэнергетической реакции, называется порогом реакции. На рис. 4.4.1а приведена энергетическая диаграмма для экзоэнергетической реакции (Q > 0), а на рис. 4.4.1б - для эндоэнергетической реакции (Q < 0). На диаграммах изображен процесс образования промежуточного возбужденного ядра 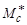и его распад с образованием частиц B и b для обоих типов реакций. ε_а = M_A + m_a - M_c – есть энергия связи частицы а, а ε_b = M_B + m_b - M_c – частицы b относительно промежуточного ядра М_с соответственно.

Получим энергию (4.2.2) возбужденния промежуточного ядра

,

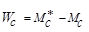(4.5.25)

где массы основного и возбужденного состояний промежуточного ядра выражены в энергетических единицах, а звездочка означает возбужденное состояние.

Пусть ядро-мишень А покоится. Запишем законы сохранения энергии и импульса для первой стадии реакции

a + A ® С *

(4.5.26)

- образования промежуточного ядра:

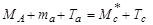, Рa = Рс.

(4.5.27)

Будем рассматривать реакции для нерелятивистского случая малых энергий налетающей частицы (Т_а ≈ 10 МэВ << m_a). Тогда

.

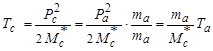(4.5.28)

Подставляя (4.5.28) в (4.5.27), получаем квадратное уравнение для нахождения :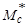

.

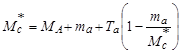(4.5.29)

В (4.5.29) последнее слагаемое составляет ничтожную долю от первых двух, так как 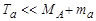. Поэтому в качестве первого приближения принимаем 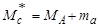. Для получения второго приближения подставляем это выражение в (4.5.29). Получаем

.

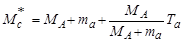(4.5.30)

Подставив (4.5.30) в (4.5.25), получим формулу

.

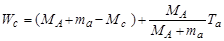(4.5.31)

Первый член в этом выражении есть ни что иное, как энергия связи 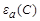частицы а по отношению к промежуточному ядру (см. (1.4.4)). Второй - суммарная кинетическая энергия 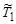частиц a и А до реакции в системе центра инерции. Итак,

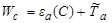
(4.5.32)

Дата добавления: 2014-01-04