Способи завдання завадостійких кодів

При завданні коду звичайно указують, які інформаційні одиничні елементи базового кодового слова і як беруть участь у формувань кожного з k перевірочних символів.

Перший спосіб завдання − описовий, коли приводиться словесно − формульний опис процедури розрахунку контрольних символів при відомих інформаційних. При завданні коду можна вказати всі дозволені для цього коду комбінації.

Наприклад, для коду з n = 5, m = 3 і k = 2 кожен перевірочний символ b_і може визначатися за правилом:

b ₁ = a ₂ 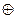a ₃, b ₂ = a ₁ 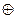a ₂,

де а_і - інформаційні символи. Комбінація такого коду записується у вигляді b ₂ b ₁ a ₃ a ₂ a _3. При завданні коду можна вказати всі дозволені для цього коду комбінації. При більш формалізованому підході це є еквівалентним завданню системи перевірочних рівнянь, що визначають правила формування перевірочних символів по відомим інформаційним:

,

де: позначка означає додавання за певним модулем, наприклад, за
модулем 2.

j − номер перевірочного символу;

і − номер інформаційного символу;

с_іj − коефіцієнти, що приймають значення відповідно до правил формування конкретних кодів, наприклад, с_іj = 1.

Другий спосіб завдання − шляхом перерахуванням кодових слів, тобто складанням таблиці − списку всіх кодових слів коду.

Приклад. У таблиці 2 представлені всі кодові слова (5, 3) − двійкового коду (a_і − інформаційні, а b_і − перевірочні символи).

Таблиця 2 Таблиця кодових слів коду (5,3)
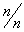
	a1	a2	a3	b1	b2

Третій спосіб завдання − у вигляді матриці, що породжує, в так званій канонічній формі. При цьому перші (праві) m стовпців цієї матриці містять по одній одиниці і утворюють одиничну матрицю. Решта стовпців указує правила формування перевірочних одиничних елементів.

Так, для приведеного прикладу двійкового коду матриця, що породжує, в канонічній формі має вигляд:

G (5, 3) =

З прикладу видно, що перші три стовпці складають одиничну матрицю

І (m, m) = ,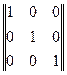

четвертий стовпець показує, що при формуванні першого перевірочного символу беруть участь другий і третій інформаційні символи. П’ятий стовпець що при нормуванні другого перевірочного символу беруть участь перший і другий інформаційні символи. Таким чином, при написанні матриці, що породжує, в канонічній формі спочатку пишуть одиничну матрицю розміром m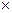m, а потім приписують до неї k стовпців, кожний з яких показує правила формування перевірочних символів. Тобто матрицю, що породжує, в канонічній формі можна позначити таким чином:

G (n, m) = .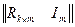

Варіантів запису матриць, що породжує, в загальному випадку досить багато.

Канонічна форма матриці, що породжує, може бути також записаною у вигляді

G (n, m) = .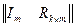

При такому способі опису процес кодування математично записується у вигляді добутку матриці-рядка, що відображає вихідну кодову комбінацію, на матрицю, що породжує. (При виконанні всіх математичних перетворень додавання здійснюється по модулю 2). Припустимо, що вихідна кодова комбінація записана так:

А = .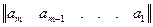

Тоді процес кодування запишеться у вигляді

F = А 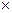G (n, m) = b_kb_{k -1}… b ₁ a_ma_{m -1…} a ₁,

де, як і раніше, b_і (і = 1, 2,... k) – перевірочні, а a_і (і = 1, 2,..., m) – інформаційні символи.

В результаті кодування одержимо комбінацію, де перші m символів − інформаційні (a_і), а останні k символів − перевірочні (b_і). Наприклад, закодуємо кодову комбінацію A = 1011 кодом (7, 4) з матрицею, що породжує,

G (7, 4) = .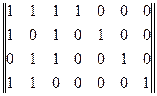

Для цього перемножимо матриці A і G: F = A 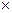G (7, 4). Одержимо

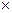
F = 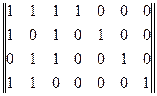= 0101011,

де перші чотири символи (1011) − інформаційні, а останні три (010) − перевірочні.

При декодуванні на приймальній стороні здійснюється стільки ж перевірок, скільки виконувалося і на передаючій, Кожна перевірка включає, окрім інформаційних символів, перевірочні символи.

Результат цих перевірок указує або тільки на наявність або відсутність спотворення, або ще й номер спотвореного символу.

2. Двійкові коди з перевіркою на парність або на непарність (контроль по модулю 2)

Як відомо, у загальному випадку, вираз для розрахунку контрольної ознаки має вигляд:

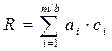(mod Р), (5)

де Р – значення обраного модуля. В коді з контролем по модулю 2 додавання здійснюється порозрядно, тобто 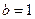, додавання здійснюється за модулем Р = 2, 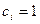для усіх значень і.

При побудові таких кодів передана послідовність символів розбивається на групи – базові кодові слова (БКС). У найпростішому випадку при кодуванні в кожному базовому кодовому слові розраховується контрольна ознака (контрольний біт) шляхом складання по модулю 2 всіх двійкових символів БКС. Контрольна ознака (контрольний біт) записується в кінці БКС. При контролі на парність, в результаті цього, число одиниць в БКС доводиться до парного. Так, кодова комбінація 01110 в результаті кодування перетвориться в комбінацію 011101.

Варіантом цього способу контролю цілісності є контроль на непарність, коли при кодуванні в кінець БКС як контрольна ознака (контрольного біта) дописується інверсне значення результату складання по модулю 2 всіх двійкових символів даного БКС. В результаті цього, при контролі на непарність, число одиниць в БКС доводиться до непарного. Так, кодова комбінація 01010 в результаті кодування перетвориться в комбінацію 010101.

При декодуванні процедура (5) здійснюється знов, але по відношенню до усіх символах із перевірочними включно, тобто для символів. В наслідок цього обраховується контрольна ознака

(mod Р).

Неважко зрозуміти, що в разі відсутності спотворень величина 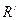є такою, що дорівнює нулю, а при їх наявності – відмінна від нуля. Це і є синдромом спотворень. Зрозуміло, що корегування виявлених спотворень є неможливим. Окрім того, виходячи з розглянутого, слід зробити висновок, що спотворення, що виникли в парному числі символів, залишаються непоміченими.

Дата добавления: 2014-01-04