Двійкові матричні коди

Основним недоліком описаних вище кодів є невиявлення спотворень парної кратності, тому такі коди знаходять застосування в тих ланках АС, де найбільш вірогідними є одиночні спотворення, наприклад в ланці ТКМ - ЕОМ. Якщо ж спотворення мають тенденцію до групування, то для виявлення групових спотворень БКС (кодові комбінації) записуються у вигляді матриці:

а ₁₁ а ₁₂ а ₁₃… а _{1 s}

а ₂₁ а ₂₂ а ₂₃… а _{2 s}

…………………

a_{t 1} а_{t 2} а_{t 3}… а_ts

______________

c ₁ c ₂ c ₃ … c_s,

Потім здійснюється перевірка на парність (або на непарність) стовпців отриманої матриці. За наявності одного групового спотворення, завдовжки не більш s (s − число стовпців матриці), в кожну перевірку входитиме не більше ніж один спотворений символ (відбудеться декореляція спотворень). Якщо спотворення незалежні, то даний код є еквівалентним коду з перевіркою на парність по стовпцям, коли для кожного із s стовпчиків як і в коді з контролем на парність обраховуються значення своя контрольна ознака:

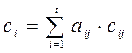(mod Р),

при порозрядному додаванні і Р = 2, 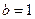, 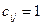для усіх значень і, j.

Якщо ж спотворення корельовані, то за рахунок перевірки символів, що рознесені (за рахунок декореляції спотворень), даний код буде більш завадостійким. Недоліком такого коду є деяке ускладнення кодуючих і декодуючих пристроїв. Декореляція спотворень здійснюється і в тому випадку, якщо перевірку на парність здійснювати по рядках чи по діагоналях матриці. З погляду завадостійкості цей код є аналогічним попередньому.

Для підвищення здатності із визначення наявності спотворень перевірка на парність (непарність) може бути проведена одночасно по стовпцях і діагоналях або по рядках і стовпцях.

Останній код називають матричним. У даному коді (при використанні контролю на парність) перевірочні символи формуються за наступними правилами:

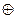а ₁₁ а ₁₂ а ₁₃ … а _{1 s} b ₁ b_i = а _{1 i} а _{2 i 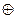……….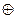} а _{l s}

а ₂₁ а ₂₂ а ₂₃ … а _{2 s} b ₂ c_j = а _{1 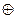j} а _{2 j 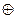……….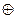} а _{2 s}

………………

а_{t 1} а_{t 2} а_{t 3} … а_ts b_t

c ₁ c ₂ c ₃ c_s

де t − число рядків матриці; s − число стовпців матриці; m = st, n = st + s + t.

Для підвищення здатності по виявленню спотворень перевірці на парність піддається також послідовність перевірочних символів, одержаних при перевірці до рядкам або стовпцям. При такій побудові коду будуть знайдені всі одиночні, подвійні і потрійні спотворення, а також всі непарні спотворення і деякі парні спотворення більшої кратності.

Матричний код знаходить: спотворення до кратності l = 3 включно (одиночні, подвійні, потрійні), всі непарні спотворення і деякі парні спотворення більшої кратності (четверні, шестерні і т.д.) при умові, що кількість спотворень в одному й тому ж рядку чи стовпчику є непарною. Поодинокі спотворення гарантовано виправляються.

Іноді до перевірок по рядках і стовпцях додають перевірки по діагоналях. Це ще більше покращує здібності коду, що виявляє. Для боротьби з груповими спотвореннями довжина рядка матриці (кількість стовпців) повинна бути не менше половини довжини пакету спотворень b_сп, тобто s ≥ b_сп /2.

Недоліком коду є додаткова затримка в передачі інформації за рахунок часу формування матриці.

Матричні коди доцільно використовувати при кодових комбінаціях великої довжини.

Дата добавления: 2014-01-04